0615

Quantitative Characterization of the Motion Sensitivity of Stimulated Echo Diffusion-weighted Imaging in the Liver
Yuxin Zhang1,2, James Holmes2, Kevin Johnson1,2, Ty Cashen3, and Diego Hernando1,2

1Medical Physics, University of Wisconsin Madison, Madison, WI, United States, 2Radiology, University of Wisconsin Madison, Madison, WI, United States, 3Global MR Applications & Workflow, GE Healthcare, Madison, WI, United States

Synopsis

STimulated Echo (STE) DWI is able to provide high b values with moderate echo times by increasing the mixing time (TM). However, long TM in STE-DWI also lead to increased sensitivity to bulk motion. To understand the tradeoff between SNR and motion sensitivity of STE DWI, this study assessed the quantitative relationship between TE, TM, and motion sensitivity in the liver with simulation and in-vivo experiments. As a result, the SNR and high motion sensitivity present an important trade-off with STE-DWI. In addition, when moment-nulling is used to compensate motion, the advantage of decreased TE from STE will be lost.

Introduction

Compared to conventional Spin Echo (SE) diffusion-weighted imaging (DWI), STimulated Echo (STE)-DWI provides high b values with reduced echo times (TEs) by increasing the mixing time (TM). Thus, STE-DWI may provide higher SNR in tissues with short T2 and relatively long T1, eg: in liver imaging (liver T2~34ms and T1~800ms at 3T) [4]. Further, there is interest in characterizing restricted diffusion by varying the diffusion time (which can be controlled through TM) in liver imaging [1-3]. However, long TM in STE DWI increases sensitivity to bulk motion, which can result in artifacts in the liver due to the presence physiological motion (eg: respiratory and cardiac motion). The tradeoff between SNR and motion sensitivity of SE versus STE DWI is not well understood. Therefore, the purpose of this work is to quantitatively assess relationships between TE, TM, and motion sensitivity in STE-DWI of the liver, as a necessary step for the optimization of SNR and reproducibility of liver STE-DWI.

Theory

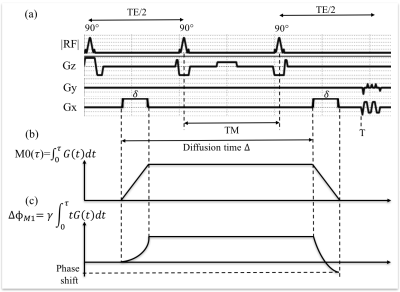
The STE DWI sequence, as shown in Fig.1, is able to reduce TE for a given b-value by storing the magnetization along the longitudinal axis while spins are experiencing motion:$$M0(\tau)=\int_{0}^{\tau}G(t)dt,(Eq.1)$$ $$b=\gamma\int_{0}^{T}(M0(\tau))^{2}d{\tau},(Eq.2)$$ where $$$\gamma$$$=42.58MHz/T, G(t) is the diffusion encoding waveform and T is the total diffusion encoding time.

Analogously, the motion sensitivity of a diffusion MRI sequence can be characterized by its first order moment, defined as:$$M1=\int_{0}^{T}G(t)tdt.(Eq.3)$$ For a spin moving with velocity v, the first order moment will result in a phase shift given by$$$\Delta\phi$$$,$$\Delta\phi_{M1}=v\gamma\int_{0}^{T}G(t)tdt.(Eq.4)$$ As an example, when using STE-DWI with monopolar diffusion gradients, this phase shift can be written as$$\Delta\phi_{M1}=v\gamma\delta{G}\Delta=v\gamma\delta{G}(TM+t_{sep}), (Eq.5)$$where $$$t_{sep}$$$ accounts for the width of the diffusion pulse and the RF pulses. In this case, when TM is increased, $$$\Delta\phi_{M1}$$$ will also be increased, which results in larger motion induced signal loss in the presence of spins moving with different velocities within the voxel.

Methods

Simulation: Both diffusion-weighted SE and STE signals were simulated in Matlab with T1=800ms, T2=34ms (normal liver) and T2=11ms (mild liver iron overload), ADC=1.3mm2/s, Gmax=49mT/m, maximum Slew-Rate=100T/m/s, T_90=5.3ms, T_180=6ms and readout-to-echo time=11ms. Different maximum b-values were simulated with TE minimized for each b-value. Different TMs were also used for STE sequences. SNR of SE and STE signals are calculated by$$SNR_{SE}=\frac{Ae^{-\frac{TE}{T2}}e^{-bADC}}{\sigma}(Eq.6)$$and$$SNR_{STE}=\frac{Ae^{-\frac{TM}{T1}}e^{-\frac{TE}{T2}}e^{-bADC}}{2\sigma}.(Eq.7)$$The first moment motion induced phase shift is calculated with Eq.5 assuming v=1cm/s.

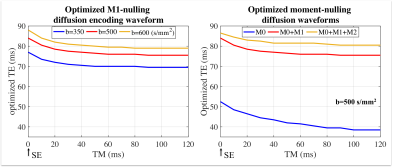
Motion-compensation simulation: To reduce the motion induced signal voids in STE DWI, motion-compensated diffusion gradient waveforms were incorporated into the STE-DWI sequence. These gradient waveforms, which are based on the recently proposed Convex Optimized Diffusion Encoding (CODE) algorithm [4], enable nulling of the first-order and second-order motion moments (M1 and M2, respectively). In this work, STE-DWI acquisitions including nulling of M0 (standard), M0+M1, and M0+M1+M2, respectively, were simulated. Different TMs from 0 to 120ms were considered, where TM=0ms implies a spin echo sequence.

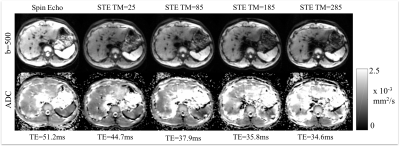
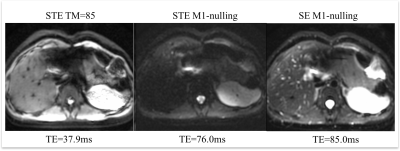
In-vivo evaluation: With IRB approval and informed consent, liver diffusion-weighted images were acquired from a healthy volunteer (T2=23.8ms) with a 30-channel torso coil in a 3T scanner (GE Healthcare, Waukesha, WI). DWI acquisitions included: SE-DWI, STE-DWI with several values of TM=[25, 85, 185, 285]ms, SE with M0+M1-nulling and STE (TM=85ms) with M0+M1-nulling. The actual TE of each sequence is shown in Fig.4 and Fig.5. Other acquisition parameters were FOV=32cm$$$\times$$$32cm, resolution=2.5mm$$$\times$$$2.5mm, slice thickness=6cm, b=[100, 500] s/mm2 and diffusion direction = R/L. Respiratory triggering was used for each sequence.

Results

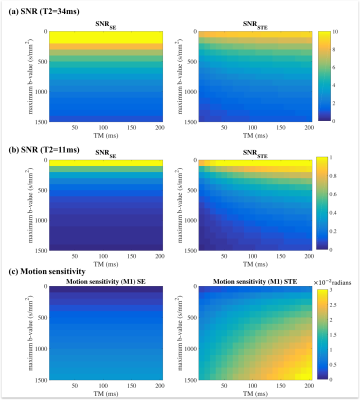
Figure 2 shows the simulated SNR and motion sensitivity of SE and STE signals. Note that STE only has higher SNR when T2 is very short, however, STE has much larger motion sensitivity than SE. The phase shift introduced by motion increases nearly linearly with increasing TM. The relationship of optimized echo time over different TM with motion-compensated waveforms is shown in Figure 3. Importantly, the main potential advantage of STE over SE (shorter TEs attainable by increasing TM) is lost when including motion compensation. Images and ADC maps with SE and STE of different TM in the volunteer (Figure 4) are in good agreement with the results from the simulation. Figure 5 presents an example of DWI with first-moment motion compensation using SE and STE.

Discussion

Although STE-DWI can provide important information of diffusion-time-dependent restricted diffusion, the SNR and high motion sensitivity present an important trade-off. However, when moment-nulling is used to compensate motion, the advantage of decreased TE from STE will be lost.

Conclusion

Stimulated Echo DWI presents a trade-off between SNR and motion sensitivity. To use STE in the liver, optimal combinations of mixing time and b-value should be considered and the presence of motion artifacts (signal voids) should be carefully assessed.

Acknowledgements

This study is supported by NIH-NIDDK Wisconsin Multidisciplinary K12 Urologic Research Career Development Program K12DK100022 (PD: D. Bjorling). The authors would like to acknowledge research support from GE Healthcare.

References

[1] Zhang, H., Sun, A., Li, H., Saiviroonporn, P., Wu, E. X., & Guo, H. (2017). Stimulated echo diffusion weighted imaging of the liver at 3 Tesla. Magnetic resonance in medicine, 77(1), 300-309.

[2] Zhang, H., Wu, E. X., & Guo, H. (2015). Efficient fat suppression by slice-selection gradient reversal in stimulated echo diffusion weighted liver imaging. In ISMRM 23rd Annual Meeting & Exhibition cum SMRT 24th Annual Meeting Proceedings.

[3] Zhou, I. Y., Gao, D. S., Chow, A. M., Fan, S., Cheung, M. M., Ling, C., etc. (2014). Effect of diffusion time on liver DWI: An experimental study of normal and fibrotic livers. Magnetic resonance in medicine, 72(5), 1389-1396.

[4] De Bazelaire, C. M., Duhamel, G. D., Rofsky, N. M., & Alsop, D. C. (2004). MR imaging relaxation times of abdominal and pelvic tissues measured in vivo at 3.0 T: preliminary results. Radiology, 230(3), 652-659.

[5] Aliotta, E., Wu, H. H., & Ennis, D. B. (2017). Convex optimized diffusion encoding (CODE) gradient waveforms for minimum echo time and bulk motion–compensated diffusion-weighted MRI. Magnetic resonance in medicine, 77(2), 717-729.

Figures

Figure 1. Stimulated echo DWI sequence profile and the phase accumulation. (a) Stimulated echo diffusion weighted imaging pulse sequence, where Δ is the diffusion time and δ is the duration of diffusion encoding lobe. The slew rate of the diffusion encoding gradients is assumed to be infinity for illustration purpose. (b) Zero moment (M0) of the diffusion encoding waveform, the integral of the square of which is proportional to the b-value. (c) First moment motion induced phase shift under motion sensitive diffusion encoding.

Figure 2. Simulation results of the SNR and the phase shift induced by the first moment motion with SE and STE sequences, where (a) SNR with T2=34ms, which represents the signal from normal liver; (b) SNR with T2=11ms, which represents the signal from liver with mild iron overload and (c) the phase shift induced by the first moment (M1) motion sensitivity. When dispersion of motion exists within a voxel, the higher M1 motion sensitivity of STE sequences will lead to more serious artifacts (signal voids) compared with SE DWI.

Figure 3. Optimized echo time over TM with CODE motion compensation method. (a) TE over TM of optimized M1-nulling diffusion encoding waveforms with different b-values; (b) TE over TM of optimized M0-, M0+M1- and M0+M1+M2- nulling diffusion encoding waveforms with b=500 s/mm2. TM=0 represents optimized waveforms with Spin Echo sequence. The use of STE DWI is able to decrease the TE by more than 13ms with increasing TM without motion compensation, but only 9ms maximum decrease with motion compensation.

Figure 4. Example liver DW images and ADC maps of SE and STE sequences with different TM. Images were scaled to the same window level. With increasing TM, we have more severe signal voids from motion, and larger ADC bias and heterogeneity throughout the liver. As predicted, STE DWI does not lead to increased SNR compared to the SE DWI.

Figure 5. Example DW-images (b=500 s/mm2) of standard (non-motion compensated) STE DWI (TE=37.9ms, TM=85ms), as well as M0+M1-nulled STE DWI (TE = 76ms, TM=85ms) and SE DWI (TE=85ms). STE with M0+M1-nulling is able to reduce the signal voids from motion, but results in substantially longer TE and lower SNR compared to standard STE.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0615