0576

Scan-specific Robust Artificial-neural-networks for k-space Interpolation (RAKI): Database-free Deep Learning Reconstruction for Fast Imaging
Mehmet Akçakaya1,2, Steen Moeller2, Sebastian Weingärtner1,2,3, and Kâmil Uğurbil2

1Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Computer Assisted Clinical Medicine, University Medical Center Mannheim, Heidelberg University, Mannheim, Germany

Synopsis

Long scan times remain a limiting factor in MRI. Accelerated imaging is commonly required, with parallel imaging being the most clinically used approach. Recently, machine learning has also been applied to accelerated MRI reconstruction, where the focus has been on training regularizers on large datasets. In this work, we develop a scan-specific deep learning k-space method for reconstruction of undersampled data. The proposed method, Robust Artificial-neural-networks for k-space Interpolation (RAKI) learns a non-linear convolutional neural network from limited autocalibration signal. Phantom, cardiac and brain data show that RAKI improves upon the reconstruction quality of linear k-space interpolation-based parallel imaging methods.

Introduction

Parallel imaging is routinely used in most clinical MRI scans, allowing a trade-off between scan-time and SNR1-3. GRAPPA3 is a commonly used technique that performs linear interpolation in k-space using shift-invariant convolutional kernels, determined from limited autocalibration signal (ACS). Following its success in many areas of image processing, machine learning (ML) has also recently been applied to reconstruction in accelerated MRI. So far, the focus has been on generating advanced regularizes by training on large amounts of datasets, with promising results4-8. However, these methods require large databases of MR images for rigorous training, and rely on patterns across the training set, rather than within each individual image.

In this study, we develop a scan-specific deep learning k-space method for reconstruction of undersampled data. The proposed method, called Robust Artificial-neural-networks for k-space Interpolation (RAKI) learns a non-linear convolutional neural network (CNN) from limited ACS data. This extends on the linear convolutional kernels of GRAPPA, while performing both training and reconstruction on a per image basis.

Theory

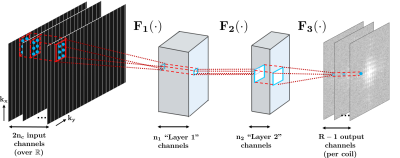
CNNs are mathematical models that estimate a function, by combining multiple layers of simple modules, such as convolutions and point-wise nonlinear operators9. In this study, we employ a CNN to estimate a multi-coil MRI reconstruction with a three-layer architecture, as depicted in Figure 1: F1(x) = ReLU(w1*x), F2(x) = ReLU(w2*x), F3(x) = w3*x, where * denotes convolution; w1,w2,w3 are convolutional kernels, and ReLU(x) = max(x, 0) is the rectified linear unit. The network has 2nc input channels (nc: number of coils, factor 2: due to complex k-space being mapped to real field). Kernel sizes in this study are: 5×2×2nc×32 for w1, 1×1×32×8 for w2, 3×2×8×(R–1) for w3, where R is the uniform acceleration rate. The kernels, {w1,w2,w3} are estimated from the ACS region with mean squared error (MSE) as the loss function. Gradient descent with back-propagation10 and momentum11 is used for estimation.

Methods

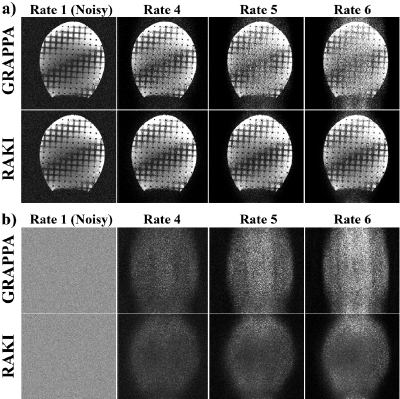
Phantom imaging was performed at 3T with a 32-channel head-coil, using a FLASH sequence to image a head-shaped phantom (FOV=220×220mm2, resolution=0.7×0.7mm2, thickness=4mm). Complex Gaussian noise was added, and data was retrospectively undersampled to R=4,5,6. RAKI and GRAPPA reconstructions were performed, and normalized MSE (NMSE) was calculated.

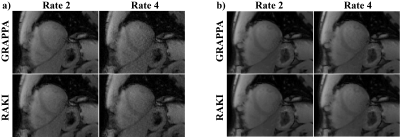
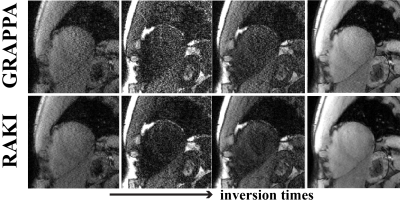
Cardiac imaging was performed at 3T with a 30-channel body-coil. SAPPHIRE myocardial T1 mapping12 was acquired in 4 subjects with 11 T1-weighted images. Acquisitions (FOV=300×300mm2) were performed at two resolutions: i) 1.7×1.7mm2, thickness=8mm, R=2, retrospectively undersampled to R=4, ii) 1.1×1.1mm2, thickness=6mm, R=5. These datasets were used to study the robustness of RAKI across different contrasts, where all 11 images were reconstructed using a CNN calibrated from only one T1-weighted image.

Brain imaging was performed at 7T using a 32-channel head coil. 3D-MPRAGE was acquired on a patient, with FOV=230×250×154mm3, resolution=0.6×0.6×0.6mm3, R=3, retrospectively undersampled to R=6. Data was reconstructed with RAKI and GRAPPA, testing robustness to blurring at high resolutions.

Results

In phantom at R=4,5,6, RAKI shows less noise amplification than GRAPPA (Figure 2, NMSE: GRAPPA:0.51,0.66,0.89; RAKI:0.46,0.47,0.52).

In SAPPHIRE T1 mapping image quality is visually comparable between GRAPPA and RAKI at R=2, while there are minor improvements in noise performance at R=4 (Figure 3). These improve precision in the T1 maps (10% reduced variability). For both acceleration rates RAKI successfully reconstructs varying image contrast from a single training ACS, maintaining quantitative accuracy (difference of estimated T1 <1%). At higher resolution and R=5, visual improvement with RAKI over GRAPPA becomes apparent in T1-weighted images (Figure 4), and T1 maps exhibit 37% improved spatial variability.

For the high-resolution MPRAGE acquisition, at R=3, there is no visual difference, but at R=6, GRAPPA suffers from pronounced noise amplification, whereas RAKI demonstrates better noise tolerance (Figure 5). No blurring artifacts are observed with either method.

Discussion

In this work, we utilize CNNs to estimate missing k-space lines for accelerated MRI. Similar to existing parallel imaging reconstructions, all learning is performed on a small set of ACS, deviating from the ML trend of utilizing large databases4-8.

Results indicate improved noise performance at high resolutions compared to GRAPPA. Additionally, our data exhibits robustness against contrast variations, indicating that the non-linear k-space interpolation scheme is not over-fitting, and can be efficiently applied to multi-contrast imaging (e.g. perfusion, diffusion, quantitative mapping).

Our reconstruction extends naturally to other approaches utilizing k-space interpolation, e.g. 3D13,14, simultaneous multi-slice15,16, random undersampling17 and non-Cartesian sampling18. These extensions are beyond the scope of the current study and will be explored in future work.

Conclusion

The proposed RAKI reconstruction uses a scan-specific deep learning approach utilizing CNNs trained on limited ACS data to improve upon the reconstruction quality of linear k-space interpolation-based methods.

Acknowledgements

Funding: Grant support: NIH R00HL111410, NIH P41EB015894, NIH U01EB025144, NIH R01NS085188, NIH P30NS076408, NIH P50NS098573 and NSF CAREER CCF-1651825.

References

1. Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn Reson Med 1997;38(4):591-603.

2. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42(5):952-962.

3. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). 2002;47(6):1202-10.

4. Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating Magnetic Resonance Imaging Via Deep Learning. 2016 April; Prague. IEEE International Symposium on Biomedical Imaging (ISBI). p 514-517.

5. Yang Y, Sun J, Li H, Xu Z. Deep ADMM-Net for Compressive Sensing MRI. 2016; Barcelona. Advances in Neural Information Processing Systems (NIPS). p 10-18.

6. Hammernik K, Knoll F, Sodickson D, Pock T. Learning a Variational Model for Compressed Sensing MRI Reconstruction. 2016; Singapore. Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM). p 1088.

7. Han YS, Yoo J, Ye JC. Deep Learning with Domain Adaptation for Accelerated Projection Reconstruction MR. preprint 2017:arXiv:1703.01135.

8. Lee D, Yoo J, Ye JC. Deep Artifact Learning for Compressed Sensing and Parallel MRI. preprint 2017:arXiv:1703.01120.

9. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature 2015;521(7553):436-444.

10. LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE 1998;86(11):2278-2324.

11. Sutskever I, Martens J, Dahl GE, Hinton G. On the importance of initialization and momentum in deep learning. 2013; Atlanta. International Conference on Machine Learning. p 1138-1147.

12. Weingartner S, Akcakaya M, Basha T, Kissinger KV, Goddu B, Berg S, Manning WJ, Nezafat R. Combined saturation/inversion recovery sequences for improved evaluation of scar and diffuse fibrosis in patients with arrhythmia or heart rate variability. Magn Reson Med 2014;71(3):1024-1034.

13. Blaimer M, Breuer FA, Mueller M, Seiberlich N, Ebel D, Heidemann RM, Griswold MA, Jakob PM. 2D-GRAPPA-operator for faster 3D parallel MRI. Magn Reson Med 2006;56(6):1359-1364.

14. Breuer FA, Blaimer M, Mueller MF, Seiberlich N, Heidemann RM, Griswold MA, Jakob PM. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magn Reson Med 2006;55(3):549-556.

15. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 2012;67(5):1210-1224.

16. Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, Ugurbil K. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magn Reson Med 2010;63(5):1144-1153.

17. Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn Reson Med 2010;64(2):457-471.

18. Seiberlich N, Ehses P, Duerk J, Gilkeson R, Griswold M. Improved radial GRAPPA calibration for real-time free-breathing cardiac imaging. Magn Reson Med 2011;65(2):492-505.

Figures

Figure 1: The three-layer CNN architecture used in this study. The first layer, F1, takes in the R-fold sub-sampled k-space of size nx×ny×2nc, as embedded into real field. The convolutional filters in this layer, w1 are of size 5×2×2nc×32. This is followed by a rectified linear unit (ReLU) operation. The second layer, F2, takes in the output of the first layer and applies convolutional filters, w2, are of size 1×1×32×8. This layer also includes a ReLU operation. The final layer of the network, F3, produces the desired reconstruction output by applying convolutional filters, w3, of size 3×2×8×R–1.

Figure 2: Results of phantom experiments. (a) Images reconstructed using GRAPPA (top row) and the proposed RAKI (bottom row) reconstructions from noisy data sets for various acceleration rates, as well as a fully-sampled noisy reference image. The noise performance of RAKI improves upon that of GRAPPA for R = 4, 5, 6. (b) The difference images for these reconstructions, as compared to the original acquisition without additional noise, confirm the observations in (a). NMSE quantification also confirms these observations: 0.51, 0.66 and 0.89 for GRAPPA versus 0.46, 0.47 and 0.52 for RAKI for R = 4, 5, 6.

Figure 3: Representative T1-weighted images from SAPPHIRE T1 mapping acquired at 1.7×1.7mm2. (a) Images with low acquisition SNR, corresponding to the shortest inversion time, at R=2, and R=4. At R=4, the noise performance improvement of RAKI over GRAPPA becomes apparent. (b) Images with high acquisition SNR, where the differences between RAKI and GRAPPA are visually minor even at R=4, with a slight improvement in the left ventricle blood pool for RAKI. A quantitative analysis of the resulting T1 maps indicate that comparable quantification is observed for the two reconstructions, except for a 10% reduced noise variability with RAKI at R=4.

Figure 4: Representative T1-weighted images acquired using the SAPPHIRE sequence at a high spatial resolution of 1.1×1.1mm2, and R=5. At this high acceleration rate, the noise improvement of RAKI over GRAPPA is observable for all images. A quantitative analysis of the resulting T1 maps indicate that the spatial variability of the myocardial T1 is improved by 37% using RAKI versus GRAPPA.

Figure 5: A central slice of the high-resolution (0.6 mm isotropic) MPRAGE acquisition, both at the acquisition acceleration R=3, as well as at a retrospective R=6. At R=3, GRAPPA (top) and RAKI (bottom) methods both successfully reconstruct the image with little residual artifacts. At R=6, GRAPPA reconstruction suffers heavily from noise amplification, whereas RAKI reconstruction exhibits improved noise tolerance without blurring artifacts.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0576