0574
ReconNet: A Deep Learning Framework for Transforming Image Reconstruction into Pixel Classification1Monash Biomedical Imaging, Monash University, Melbourne, Australia, 2School of Psychological Sciences, Monash University, Melbourne, Australia, 3Department of Electrical and Computer System Engineering, Monash University, Melbourne, Australia, 4Institute of Medicine, Research Centre Juelich, Juelich, Germany
Synopsis
A deep learning framework is presented that transforms the image reconstruction problem from under-sampled k-space data into pixel classification. The underlying target image is represented by a quantized image, which makes it possible to design a network that classifies each pixel to a quantized level. We have compared two deep learning encoder-decoder networks with the same complexity: one is a classification network and the other is a regression network. Even though the complexity of both the networks is the same, the images reconstructed using the classifier network have resulted in a six times improvement in the mean squared error compared to the regression network.
Introduction
Application of deep learning1 convolutional neural networks (CNN) have shown remarkable performance improvement in image classification. Recently, deep learning networks have been applied to image reconstruction in MRI 2-4. However, it should be noted that there is a significant difference between image classification and image reconstruction. Image classification relies on finding a probabilistic model that predicts the probability of an image being in a certain class. In contrast, CNN image reconstruction relies on finding an exact non-linear mapping between the input and output. Inspired by the ability of CNN to accurately solve classification problems,5 in this work we present a novel method of transforming an image reconstruction problem into a pixel classification problem. We compare two CNNs having the same complexity. The first network is a classification CNN which learns a probabilistic model to classify each pixel into 8-bit quantized values. The second network is a regression CNN which learns a non-linear mapping between input and output values.Methods
In order to convert the image reconstruction problem into pixel classification, the output image in the classification network is represented by an 8-bit unsigned number, resulting in 256 different grey levels. A deep learning network is designed that predicts the probability of a given pixel being in one of the 256 different classes. This effectively transforms the problem of image reconstruction into pixel classification.
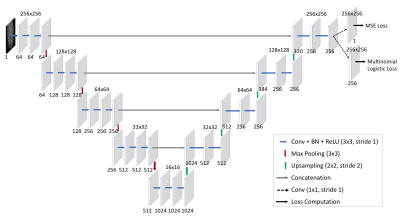
Network Architecture
We designed an encoder-decoder CNN as shown in Fig.1. The encoder consisting of series of convolution and pooling layers and a decoder consisting of series of convolution and upsampling layers. Two different variation of the Unet 6 possessing the same complexity were designed by using different loss functions as follows:
- Regression network: in which the last layers is a mean squared loss, hence the network directly predicts the floating-point representation of the reconstructed image; and
- Classification network: in which the last layer is a multinomial logistic loss, hence the network predicts the probability for each pixel being in one of the 256 different classes. The output is 8-bit unsigned integer image, which is converted to floating point by simple scaling between 0 and 1.
Data Preparation
MPRAGE images from 43 subjects were used for training and 10 subjects were used for testing. The label images for the regression network were represented in floating point while the label images for the classification network were represented in 8-bit unsigned integers. The k-space data were pseudo randomly under-sampled by a factor of 3.2 in the phase encoding direction and the images reconstructed from the under-sampled data were used as input to the network.
Training
The network was trained on 2D slices using a stochastic gradient descent algorithm in the Caffe7 deep learning library.
Results
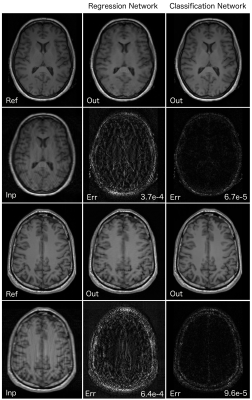
The reconstructed and error images from the under-sampled data for two of the test cases (on which the network was not trained) are shown in Fig.2. The mean squared error of the images reconstructed from the classification network was six times lower than the image reconstructed from the regression network.Discussion
The regression network learns to find the exact mapping between under-sampled and fully sampled images. However, the classification network learns the probabilistic model to classify each corrupted pixel to its true value. The probabilistic model turns out to be more robust and accurate in reconstructing the final image as is evident from the reconstruction results.
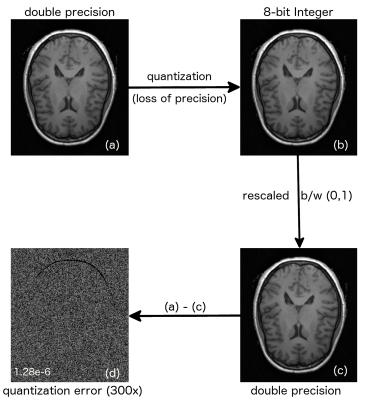
Error Analysis: For the regression network, the source of error is the prediction error arising from inaccurate learning of input-output mapping. Conversely the error in the classification network arises from two sources, including (i) the predication error arising from the network, and (ii) the second error being the quantization error arising from fixed point representation. Fig.3 demonstrates quantification of the inherent error due to quantization in the classification network. It is evident from Fig.3(d), that the quantization error (mse: 1.28e-6) is significantly lower than the overall error (mse: 6.7e-5), demonstrating that quantization has minimal effect on overall error. The quantization error can be further reduced by representing the target image using more bits at the expense of memory and computational complexity. The total error from the classification network is six times lower, which demonstrates the improved representational power of the learned probabilistic model between the input and the output. We have developed a generic design framework for deep learning reconstruction that can be readily adapted to other types of reconstruction networks such as residual learning,2 deep cascade networks3 and AUTOMAP.4
Conclusion
We have presented a novel design framework to transform the problem of image reconstruction into pixel classification. The convolutional neural network designed using this framework outperforms conventional deep learning reconstruction networks.Acknowledgements
No acknowledgement found.References
- LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015 May 28;521(7553):436-44.
- Lee D, Yoo J, Ye J C. Compressed Sensing and Parallel MRI using Deep residual learning. ISMRM 2017; 0641
- Schlemper J, Caballero J, Hajnal J.V, Price A, Rueckert D. A Deep cascade of Convolutional Neural Networks for MR Image Reconstruction. ISMRM 2017; 0643
- Zhu B, Liu J.Z , Rosen B.R, Rosen M.S. Neural Network MR Image Reconstruction with AUTOMAP: Automated Transform by Manifold Approximation. ISMRM: 0640
- Russakovsky O, Deng J, Su H, Krause J, Satheesh S, Ma S, Huang Z, Karpathy A, Khosla A, Bernstein M, Berg AC. Imagenet large scale visual recognition challenge. International Journal of Computer Vision. 2015 Dec 1;115(3):211-52.
- Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical Image Computing and Computer-Assisted Intervention 2015 Oct 5 (pp. 234-241). Springer, Cham.
- Y. Jia, E. Shelhamer, J. Donahue, S. Karayev, J. Long, R. Girshick, S. Guadarrama, and T. Darrell. Caffe: Convolutional architecture for fast feature embedding. arXiv preprint arXiv:1408.5093, 2014.
Figures