0572
Deep learning MR reconstruction with Automated Transform by Manifold Approximation (AUTOMAP) in real-world acquisitions with imperfect training1A.A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States, 2Department of Physics, Harvard University, Cambridge, MA, United States
Synopsis
Automated Transform by Manifold Approximation (AUTOMAP) is a generalized MR image reconstruction framework based on supervised manifold learning and universal function approximation implemented with a deep neural network architecture. Here we investigate the effect of significant sampling trajectory error in spiral acquisitions, where mismatch between training and runtime scanner trajectories may result in unpredictable reconstruction artifacts. We demonstrate through Monte Carlo analysis that the error in AUTOMAP reconstruction increases smoothly as a function of trajectory error, demonstrating reasonable robustness to trajectory deviation. We find these simulation results are consistent with reconstruction performance on real scanner data acquired from human subjects.
INTRODUCTION
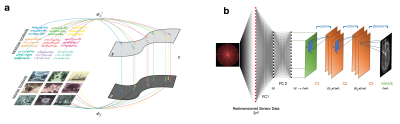
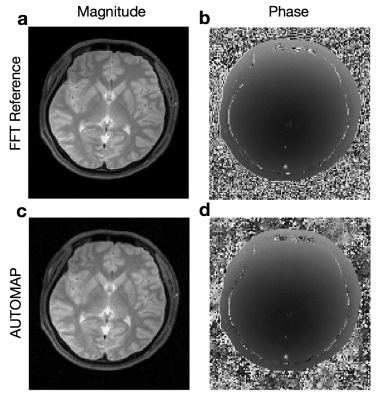
Automated Transform by Manifold Approximation (AUTOMAP)1,2 is a generalized MR image reconstruction framework based on supervised manifold learning and universal function approximation implemented with a deep neural network architecture (Figure 1). Previous work demonstrated the ability of AUTOMAP to learn the reconstruction of non-uniform Fourier data when trained on pairs of k-space and image data, without utilizing explicit operations such as the Fourier Transform, regridding, or density compensation during reconstruction, with the additional benefit of superior robustness to noise in comparison with conventional reconstruction techniques. Although the training corpus can be composed of scanner k-space collected from human subjects, a more practical method is to use a forward encoding model to generate the appropriate k-space. For MR acquisitions with small sampling errors (e.g. Turbo Spin-Echo), simulated k-space training has been shown to produce accurate reconstruction networks (Figure 2). Here we investigate acquisitions where more significant sampling trajectory errors may be present (e.g. eddy-current effects or gradient imperfections notably during spiral acquisitions), and the mismatch between the training and runtime scanner trajectories might result in unpredictable reconstruction artifacts.METHODS
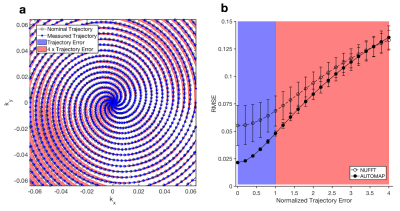
We quantified the effect of reconstruction of data that deviates from the nominal (trained) sampling trajectory using Monte Carlo simulations of varying amplitudes of trajectory error (Figure 3a) from a spiral acquisition. To examine a range of potential errors on realistic trajectories, we measured the actual trajectory during a spiral acquisition (described below) and computed the difference vectors of samples between the actual and ideal designed trajectories. These vectors were scaled to generate a set of variable-amplitude offset sampling trajectories. Trajectories from zero deviation (perfect match) to 4× the measured deviation were used to encode 100 T1-weighted ground-truth reference images from the Human Connectome Project (HCP)3 into simulated k-space data, which was reconstructed with both AUTOMAP and non-uniform FFT. Spiral k-space data was then acquired from a healthy volunteer on a Siemens 3T Prisma MRI scanner using a 32-channel head coil. A constant spiral trajectory was designed to cover a field of view of 256 x 256 mm2 with 2 x 2 mm2 in-plane resolution and 5 mm slice thickness. This was achieved using 10 spiral interleaves, each having an 8 ms readout duration which included a 1 ms rewinder, with slew rate 133 mT/m/ms and maximum gradient strength 24 mT/m; TE = 35 ms, TR = 200 ms, and flip angle = 20°. Data from the multichannel receiver head coil was SVD coil-compressed to one channel. A calibration acquisition measurement was made to measure the actual sampling trajectory4.
The AUTOMAP neural network (Figure 1) is composed of a series of fully-connected layers and convolutional layers. The fully-connected layers approximate the between-manifold projection from the sensor to image domain, representing the spatial decoding domain transform function. The convolutional layers force the image to be represented sparsely in the convolutional feature space. The AUTOMAP network was trained on phase-modulated HCP brain images with non-Cartesian encoding with the designed spiral trajectory (more details of the AUTOMAP architecture and training protocol can be found in 1). Reconstructions were compared with non-uniform FFT regridding reconstruction5 with kernel size $$$J_d$$$ = 6 samples, using code available from http://web.eecs.umich.edu/~fessler/irt/irt/.
RESULTS AND DISCUSSION
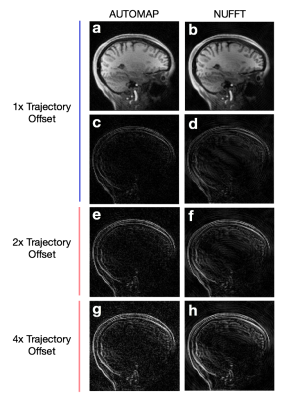
We found that the error in the AUTOMAP reconstruction increases smoothly as a function of trajectory error, similar to that in conventional NUFFT reconstruction (Figure 3b), demonstrating reasonable robustness to trajectory deviation. AUTOMAP achieved superior reconstruction accuracy compared with NUFFT out to very large trajectory errors, more than 3.5-fold larger than the measured experimental deviation (Figure 3b). Reconstructions and error maps for 1x, 2x, and 4x Trajectory Errors (based on the same reference image) are shown in Figure 4.
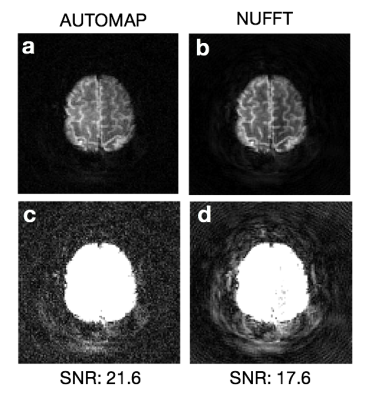
These simulation results are consistent with the reconstruction performance on real scanner data acquired from human subjects. Figure 5 shows AUTOMAP and NUFFT reconstructions of a 10-interleave spiral MR acquisition, where both methods assume the nominal trajectory. Although there is no ground truth with which to calculate reconstruction error, image SNR was measured to be higher in the AUTOMAP output (21.6 vs 17.6). Figure 5c-d displays windowed versions of Figure 5a-b, revealing coherent object-dependent and ringing artifacts in the NUFFT reconstruction (Figure 5d); these are much reduced in the AUTOMAP reconstruction, primarily exhibiting standard Gaussian white noise (Figure 5c).
If the sampling trajectory is measured during scan time, AUTOMAP can be trained upon the actual measured trajectory to achieve greater accuracy. The current implementation of AUTOMAP is trained on single trajectories; future work includes exploring strategies to embed trajectory distortion into training to produce more robust reconstruction networks.
Acknowledgements
We gratefully acknowledge Dr. Mark Michalski and the computational resources and assistance provided by the Massachusetts General Hospital (MGH) and the Brigham and Women’s Hospital (BWH) Center for Clinical Data Science (CCDS). We also acknowledge the Martinos Center for Machine Learning. B.Z. was supported by National Institutes of Health / National Institute of Biomedical Imaging and Bioengineering F32 Fellowship (EB022390). Data were provided in part by the Human Connectome Project, MGH-USC Consortium funded by the NIH Blueprint Initiative for Neuroscience Research grant; the National Institutes of Health grant P41EB015896; and the Instrumentation Grants S10RR023043, 1S10RR023401, 1S10RR019307.References
[1] Zhu, B., Liu, J. Z., Rosen, B. R., & Rosen, M. S. Image reconstruction by domain transform manifold learning. arXiv preprint arXiv:1704.08841 (2017).
[2] Zhu, B., Liu, J. Z., Rosen, B. R., & Rosen, M. S. Neural Network MR Image Reconstruction with AUTOMAP: Automated Transform by Manifold Approximation, Proc. Intl. Soc. Mag. Reson. Med., 25 p.0640 (2017)
[3] Fan, Q. et al. MGH–USC Human Connectome Project datasets with ultra-high b-value diffusion MRI. NeuroImage 124, 1108–1114 (2016).
[4] Duyn, J. H., Yang, Y., Frank, J. A. & van der Veen, J. W. Simple Correction Method for k-Space Trajectory Deviations in MRI. Journal of Magnetic Resonance 132, 150–153 (1998).
[5] Fessler, J. A. & Sutton, B. P. Nonuniform fast fourier transforms using min-max interpolation. IEEE Trans. Signal Process. 51, 560–574 (2003).
Figures