0570

DeepSPIRiT: Generalized Parallel Imaging using Deep Convolutional Neural Networks
Joseph Y. Cheng1, Morteza Mardani2, Marcus T. Alley1, John M. Pauly2, and Shreyas S. Vasanawala1

1Radiology, Stanford University, Stanford, CA, United States, 2Electrical Engineering, Stanford University, Stanford, CA, United States

Synopsis

A parallel-imaging algorithm is proposed based on deep convolutional neural networks. This approach eliminates the need to collect calibration data and the need to estimate sensitivity maps or k-space interpolation kernels. The proposed network is applied entirely in the k-space domain to exploit known properties. Coil compression is introduced to generalize the method to different hardware configurations. Separate networks are trained for different k-space regions to account for the highly non-uniform energy. The network was trained and tested on both knee and abdomen volumetric Cartesian datasets. Results were comparable to L2-ESPIRiT and L1-ESPIRiT which required calibration data from the ground truth.

Introduction

Receiver-coil arrays introduce localized spatial information that can be exploited for accelerating the scan with parallel-imaging algorithms1–5. Standard techniques rely on calibration data to characterize the localized sensitivity profiles. This data is expensive to obtain in terms of scan time (for a separate calibration scan) or effective subsampling factors (for auto-calibration approaches). Additionally, estimating sensitivity profiles can be time consuming when the channel count is high and/or when a calibration-less approach is applied6–10. We propose a generalized solution to rapidly solve the parallel-imaging problem using deep convolution neural networks (ConvNets).

Method

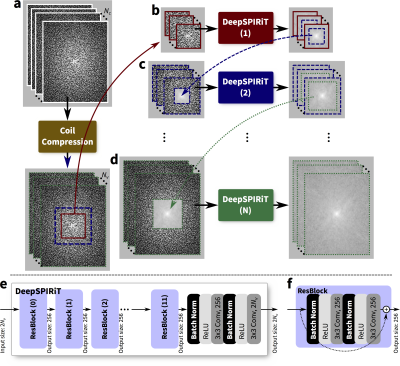
Differing from previous work of image-domain-based ConvNets11,12, we develop the infrastructure to apply ConvNets in the k-space domain to exploit known properties2,5,7,9,10,4 to enable ConvNet-based parallel imaging. Inspired by the generality of SPIRiT4, we refer to this approach as “DeepSPIRiT.”

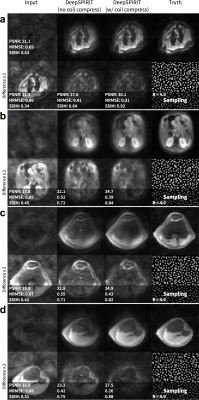
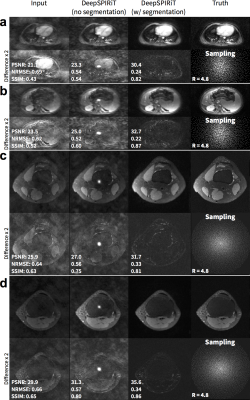
In this DeepSPIRiT framework, we introduce two main features (Figure 1). First, for faster training and for broader applicability to different hardware configurations with varying channel count and coil sizes, we normalize the data using coil compression13,14 (Figure 2). This step places the dominant virtual sensitivity map in the first channel, second dominant in the second channel, and so on. Second, to address the highly non-uniform distribution of k-space signal and the different correlation properties for different k-space regions10, ConvNets are separately trained and applied for each region. The specific setup for segmenting k-space is described in Figure 3. Each ConvNet has the same network architecture with 12 residual blocks15.

The generality of DeepSPIRiT was exploited by combining two vastly different Cartesian datasets collected with IRB approval on GE MR750 3T scanners: fully-sampled proton-density-weighted volumetric knee scans16,17 using an 8-channel knee coil, and gadolinium-contrast-enhanced T1-weighted volumetric abdomen scans using 20-channel body and 32-channel cardiac coils. Raw data were compressed to 8 virtual channels. Abdomen datasets were modestly subsampled $$$(R=1.2–2)$$$ and reconstructed using soft-gated18,19 compressed-sensing-based parallel imaging with L1-ESPIRiT5,20. For these volumetric scans, k-space data were first transformed into the hybrid $$$(x,k_y,k_z)$$$-space and separated into $$$x$$$-slices. Dataset consisted of 14, 2, and 3 knee subjects (4480, 640, and 960 slices) for training, validation, and testing, respectively. Also, 245, 21, 56 abdomen subjects (47040, 4032, and 960 slices) were included for training, validation, and testing, respectively.

For each training example, a pseudo-random uniform poisson-disc sampling mask was randomly chosen. During the training of the center 40x40 block of k-space, data was subsampled by 1.5–2. For the training for the outer portions of k-space, the subsampling factors used were 2–9. Networks were trained in TensorFlow21 using an L2-loss.

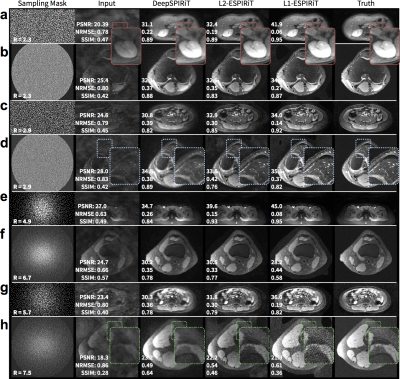
L2-ESPIRiT (with L2-regularization) and L1-ESPIRiT (with spatial wavelet regularization) were performed using BART22 for comparison. We assume that accurate sensitivity maps can always be estimated by computing ESPIRiT maps based on the fully-sampled ground truth. In practice, this information is unavailable and the sensitivity maps must be computed from a separate acquisition or through a calibration-less approach. We evaluated each reconstruction in terms of peak-signal-to-noise-ratio (PSNR), root-mean-squared-error normalized by the norm of the truth (NRMSE), and structural similarity metric23 (SSIM).

Results

For pseudo-random uniformly subsampled datasets, the use of coil compression improves DeepSPIRiT reconstruction results in terms of PSNR, NRMSE, and PSNR (Figure 2). By training models focused on specific k-space regions, the proposed DeepSPIRiT effectively reduced aliasing artifacts (Figure 4). Without k-space segmentation, a bias error was introduced in the estimated data that resulted in high-energy artifacts in the image center.

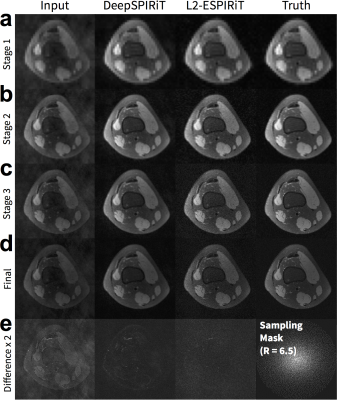
DeepSPIRiT yielded comparable results with L2-ESPIRiT and L1-ESPIRiT (Figure 5). The proposed approach was unable to fully recover higher spatial frequencies but yielded consistent results. The conventional approaches using L2-ESPIRiT and L1-ESPIRiT reconstructed sharper images; however, these approaches are sensitive to tuning of reconstruction parameters (Figure 5h) and relied on accurate sensitivity maps that were estimated from ground truth.

Discussion

The proposed approach offers several advantages. Since all training is performed offline, DeepSPIRiT is an extremely fast parallel-imaging solution for practical clinical integration. This approach eliminates the need for collecting calibration data and for estimating calibration information. Also, by reconstructing the subsampled data as a multi-channel dataset, data consistency can be explicitly enforced by replacing estimated samples with known measurements. Further, the result of DeepSPIRiT can be used as an initialization for conventional approaches: for example, the output can be used to estimate sensitivity maps or k-space interpolation kernels.

This work is focused on applying ConvNets in the k-space domain. The localized convolutions in k-space naturally generalizes the approach to both uniform and variable-density subsampling. This work can be integrated with image-domain approaches for further improvements in reconstruction accuracy.

Acknowledgements

NIH R01-EB009690, NIH R01-EB019241, and GE Healthcare.

References

  1. Sodickson, D. K. & Manning, W. J. Simultaneous acquisition of spatial harmonics (SMASH): fast imaging with radiofrequency coil arrays. Magn. Reson. Med. 38, 591–603 (1997).
  2. Griswold, M. A. et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 47, 1202–1210 (2002).
  3. Pruessmann, K. P., Weiger, M., Scheidegger, M. B. & Boesiger, P. SENSE: sensitivity encoding for fast MRI. Magn. Reson. Med. 42, 952–62 (1999).
  4. Lustig, M. & Pauly, J. M. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn. Reson. Med. 64, 457–471 (2010).
  5. Uecker, M. et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 71, 990–1001 (2014).
  6. Uecker, M., Hohage, T., Block, K. T. & Frahm, J. Image reconstruction by regularized nonlinear inversion - Joint estimation of coil sensitivities and image content. Magn. Reson. Med. 60, 674–682 (2008).
  7. Shin, P. J. et al. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn. Reson. Med. 72, 959–970 (2014).
  8. Jin, K. H., Lee, D. & Ye, J. C. A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix. arXiv:1504.00532 [cs.IT] (2015).
  9. Haldar, J. P. Low-Rank Modeling of Local k-Space Neighborhoods (LORAKS) for Constrained MRI. IEEE Trans. Med. Imaging 33, 668–681 (2014).
  10. Li, Y., Edalati, M., Du, X., Wang, H. & Cao, J. J. Self-calibrated correlation imaging with k-space variant correlation functions. Magn. Reson. Med. (2017).
  11. Hammernik, K. et al. Learning a Variational Network for Reconstruction of Accelerated MRI Data. arXiv: 1704.00447 [cs.CV] (2017).
  12. Yang, Y., Sun, J., Li, H. & Xu, Z. ADMM-Net: A Deep Learning Approach for Compressive Sensing MRI. Nips 10–18 (2017).
  13. Huang, F., Vijayakumar, S., Li, Y., Hertel, S. & Duensing, G. R. A software channel compression technique for faster reconstruction with many channels. Magn. Reson. Imaging 26, 133–141 (2008).
  14. Zhang, T., Pauly, J. M., Vasanawala, S. S. & Lustig, M. Coil compression for accelerated imaging with Cartesian sampling. Magn. Reson. Med. 69, 571–582 (2013).
  15. He, K., Zhang, X., Ren, S. & Sun, J. Identity Mappings in Deep Residual Networks. arXiv:1603.05027 [cs.CV] (2016).
  16. Epperson, K. et al. Creation of Fully Sampled MR Data Repository for Compressed Sensing of the Knee. in SMRT 22nd Annual Meeting (2013). doi:10.1.1.402.206
  17. MRI Data. Available at: http://mridata.org/. (Accessed: 14th July 2017)
  18. Johnson, K. M., Block, W. F., Reeder, S. B. & Samsonov, A. Improved least squares MR image reconstruction using estimates of k-space data consistency. Magn. Reson. Med. 67, 1600–8 (2012).
  19. Cheng, J. Y. et al. Free-breathing pediatric MRI with nonrigid motion correction and acceleration. J. Magn. Reson. Imaging 42, 407–420 (2015).
  20. Lustig, M., Donoho, D. & Pauly, J. M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 58, 1182–1195 (2007).
  21. Abadi, M. et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv:1603.04467 [cs.DC] (2016).
  22. Uecker, M. et al. BART: version 0.3.01. (2016). doi:10.5281/zenodo.50726
  23. Wang, Z., Bovik, A. C., Sheikh, H. R. & Simoncelli, E. P. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process. 13, 600–612 (2004).

Figures

Figure 1. Method overview. In a, subsampled data are first normalized through coil compression: Nc original channels becomes Nv virtual channels. In b, the k-space center block is extracted and passed into DeepSPIRiT(1). In c, a subsection of the output is combined with the original data, and a larger block of k-space is passed through another network, DeepSPIRiT(2). These steps are repeated for the entire k-space. Each DeepSPIRiT (e) is built from 12 residual blocks (f). When needed, 1x1 convolution is used in the skip connection to change the number of feature channels (dotted line in f).

Figure 2. Results with and without coil-compression for the 40x40 center test k-space data. Two representative axial abdomen slices (a and b) and two axial knee slices (c and d) are shown. The ground truth datasets (top-right) were pseudo-randomly uniformly subsampled (subsampling in bottom-right) to create input data (left). Two different networks were trained without coil compression (middle-left) and with coil compression (middle-right) for 1 day each. Both networks could reduce a significant amount of aliasing artifacts. The DeepSPIRiT network with coil compression outperformed the network without coil compression.

Figure 3. Four-stage DeepSPIRIT demonstrated on an axial slice of a volumetric knee scan. Fully-sampled k-space data was subsampled by 6.5x (sampling in e). First, a 40x40 k-space block is reconstructed using the first ConvNet (a). Then, 24x24 of the result, along with 80x80 of the subsampled k-space, is passed to the second ConvNet (b). Next, 60x60 of the result, along with 160x160 of the subsampled k-space, is reconstructed with a third ConvNet (c). Lastly, 140x140 of the result and the remaining data are used to reconstruct the full image (d). L2-ESPIRiT (third column) and fully sampled truth (last column) are shown for comparison.

Figure 4. Testing results with k-space segmentation. Two representative axial abdomen slices (a and b) and two representative axial knee slices (c and d) are shown. The ground truth datasets (top-right) were pseudo-randomly subsampled (sampling in bottom-right) to create the input data (left). Two different networks were trained without k-space segmentation (middle-left) and with k-space segmentation (middle-right). Without k-space segmentation, the trained network was unable to generalize to the entire dataset. The network introduced a bias in the estimated k-space data which resulted in high-energy artifact in the center of the images.

Figure 5. Results of both knee and abdomen datasets comparing the proposed DeepSPIRiT approach with L2-regularized parallel imaging (L2-ESPIRIT) and compressed-sensing-based parallel imaging using spatial wavelets (L1-ESPIRiT). Axial slices from abdomen (a, c, e, and g) and knee (b, d, f, and h) were retrospectively subsampled using pseudo-random uniform (a–d) and variable-density (e–h) masks. DeepSPIRiT consistently reduced aliasing artifacts and yielded comparable results to standard techniques of L2-ESPRIiT and L1-ESPIRiT.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0570