0569
Transfer learning for reconstruction of accelerated MRI acquisitions via neural networks1Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey, 2National Magnetic Resonance Research Center (UMRAM), Bilkent University, Ankara, Turkey, 3Neuroscience Graduate Program, Bilkent University, Ankara, Turkey
Synopsis
Neural network architectures have recently been proposed for reconstruction of undersampled MR acquisitions. These networks contain a large number of free parameters that typically have to be trained on orders-of-magnitude larger sets of fully-sampled MRI data. In practice, however, large datasets comprising thousands of images are rare. Here, we propose a transfer-learning approach to address the problem of data scarcity in training deep networks for accelerated MRI. Results show that networks obtained via transfer-learning using only tens of images in the testing domain achieve nearly identical performance to networks trained directly in the testing domain using thousands of MR images.
Introduction
Neural network (NN) architectures have recently been proposed for reconstruction of undersampled MR acquisitions1–10. In the NN framework, a network is trained off-line using a relatively large set of fully-sampled MRI data, and the trained network is later used for on-line reconstruction of undersampled data. Previous studies typically used an extensive database of MR images comprising several tens to hundreds of subjects5,7,8,10. Unfortunately, large databases such as those provided by the Human Connectome Project may not be readily available in many applications. In turn, data scarcity renders NN-based reconstructions suboptimal and reduces their availability to many end users. In this study, we propose a transfer-learning approach to address the problem of data scarcity in NN-based accelerated MRI. In the training domain where thousands of images are available, the network is trained to reconstruct reference images from zero-filled reconstructions of undersampled data. In the testing domain where data are scarce, the trained network is then fine-tuned end-to-end using only few tens of images. With this approach, we demonstrate successful domain transfer between MR images of different contrasts, and between natural and MR images.
Methods
In the NN framework for accelerated MRI, a network is trained via a supervised learning procedure, with the aim to find the set of network parameters that yield accurate reconstructions from undersampled acquisitions1–10. This procedure is performed on a large set of training data (with samples), where fully-sampled reference acquisitions are retrospectively undersampled. Here, we leveraged a deep CNN architecture with multiple subnetworks cascaded in series interleaved with data-consistency projections3. We trained each subnetwork by minimizing the following loss function:
$$\underset{\theta}{\mathrm{argmin}}\sum_{n=1}^{N_{train}}\frac{1}{N_{train}}\left\lVert{C(x_{un};\theta)-x_{refn}}\right\rVert_{2}+\sum_{n=1}^{N_{train}}\frac{1}{N_{train}}\left\lVert{C(x_{un};\theta)-x_{refn}}\right\rVert_{1}+\gamma_\phi\left\lVert\theta\right\rVert\quad(1)$$
where $$$x_{un}$$$ represents the Fourier reconstruction of nth undersampled acquisition, $$$x_{refn}$$$ represents the respective Fourier reconstruction of the fully-sampled acquisition, $$$C(x_{un};\theta)$$$ denotes the output of the network given the input image $$$x_{un}$$$ and the network parameters $$$\theta$$$. While training the subnetwork, the parameters of preceding subnetworks were taken to be fixed. The optimization problem in Eq. 1 was solved using the Adam algorithm11 for 20 epochs with a learning rate of η=10-4. Connection weights were L2-regularized with a regularization parameter of $$$\gamma_\phi$$$=10-6. We trained three separate networks using 4000 natural images (ImageNet dataset), 4000 T1-weighted images and 4000 T2-weighted images (MIDAS dataset)12,13. To examine the success of the proposed approach, we then fine-tuned each network end-to-end using [0 40] images in the testing domain. (Note that the training and testing domains were distinct.) All optimization procedures for fine-tuning were identical to the original training except for a lower learning rate of 10-5 and a total of 150 epochs. Independent datasets of 628 T1-weighted and 640 T2-weighted images were reserved for evaluating network performance. For all training and testing procedures, images were undersampled in the Fourier domain via variable-density Poisson-disc sampling 4-fold acceleration14. Conventional CS reconstructions were also computed as a reference15.
Results
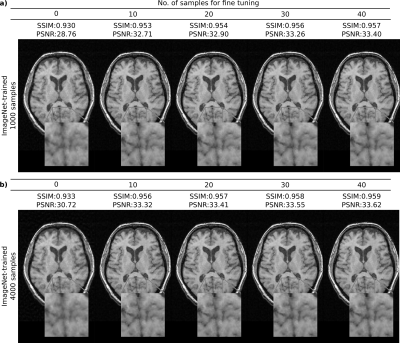
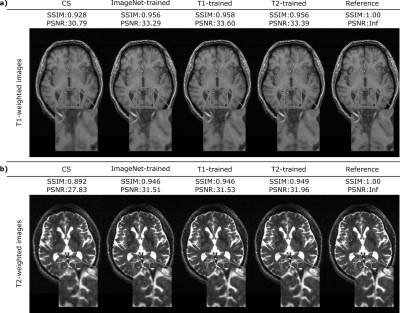
Figure 1 shows the interaction between the number of training and fine-tuning samples when the ImageNet-trained network was used to reconstruct representative T1-weighted acquisitions. Fine-tuning the network on just 10-20 samples enhances the quality of the reconstruction and increases the PSNR by up to 4 dB when training dataset size is 1000, and up to 3 dB when the training dataset size is 4000. Figure 2 displays the representative reconstructions of T1-weighted and T2-weighted acquisitions obtained via the ImageNet-trained, T1-trained, and T2-trained networks (with 4000 training and 20 fine-tuning samples). For the T1-weighted acquisition, the ImageNet-trained network yields nearly identical reconstruction quality to the other domain-transferred (i.e., T2-trained) and the domain-preserved (i.e., T1-trained) network. The same observation is true for the T2-weighted acquisitions. These observations are also supported by quantitative assessments of image quality. For T1-weighted acquisitions, the ImageNet-trained network achieved 35.59±2.72 dB PSNR (mean±std across 628 test images) with nearly identical performance to 35.89±2.63 dB by the domain-preserved T1-trained network. It also outperformed CS that yielded 33.36±3.31 dB PSNR. For T2-weighted acquisitions, the ImageNet-trained network achieved 35.20±1.85 dB PSNR (mean±std across 640 test images) again with nearly identical performance to 35.51±1.87 dB by the domain-preserved T2-trained network. It also outperformed CS that yielded 31.98±2.14 dB PSNR.Conclusion
In this work, we proposed a transfer-learning approach for accelerated MRI that adapts a neural network trained in a domain with ample data by using only a small dataset in the testing domain. We demonstrate successful domain transfer between T1- and T2-weighted, and between natural and MR images. The proposed approach significantly improves the performance of neural-networks for accelerated MRI without the need for collection of extensive imaging datasets.Acknowledgements
This work was supported in part by a Marie Curie Actions Career Integration Grant (PCIG13-GA-2013-618101), by a European Molecular Biology Organization Installation Grant (IG 3028), by a TUBA GEBIP 2015 fellowship, and by a BAGEP 2017 fellowship.References
1. Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating magnetic resonance imaging via deep learning. IEEE 13th International Symposium on Biomedical Imaging (ISBI); 2016. pp. 514–517. doi: 10.1109/ISBI.2016.7493320.
2. Han YS, Yoo J, Ye JC. Deep Learning with Domain Adaptation for Accelerated Projection Reconstruction MR. arXiv Prepr arXiv:1703.01135. 2017.
3. Schlemper J, Caballero J, Hajnal J V., et al. A Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction. arXiv Prepr arXiv:1703.00555. 2017.
4. Hammernik K, Klatzer T, Kobler E, et al. Learning a Variational Network for Reconstruction of Accelerated MRI Data. arXiv Prepr arXiv:1704.00447. 2017.
5. Yu S, Dong H, Yang G, et al. Deep De-Aliasing for Fast Compressive Sensing MRI. arXiv Prepr arXiv:1705.07137. 2017.
6. Yang Y, Sun J, Li H, et al. ADMM-Net: A Deep Learning Approach for Compressive Sensing MRI. arXiv Prepr arXiv:1705.06869. 2017.
7. Mardani M, Gong E, Cheng JY, et al. Deep Generative Adversarial Networks for Compressed Sensing Automates MRI. arXiv Prepr arXiv:1706.00051. 2017.
8. Zhu B, Liu JZ, Rosen BR, et al. Image reconstruction by domain transform manifold learning. arXiv Prepr arXiv:1704.08841. 2017.
9. Quan TM, Nguyen-Duc T, Jeong W-K. Compressed Sensing MRI Reconstruction with Cyclic Loss in Generative Adversarial Networks. arXiv Prepr arXiv:1709.00753. 2017.
10. Hyun CM, Kim HP, Lee SM, et al. Deep learning for undersampled MRI reconstruction. arXiv Prepr arXiv:1709.02576. 2017.
11. Kingma DP, Ba JL. Adam: A Method for Stochastic Optimization. arXiv Prepr arXiv:1412.6980. 2014.
12. Russakovsky O, Deng J, Su H, et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015;115:211–252. doi: 10.1007/s11263-015-0816-y.
13. Bullitt E, Zeng D, Gerig G, et al. Vessel tortuosity and brain tumor malignancy: A blinded study. Acad. Radiol. 2005;12:1232–1240. doi: 10.1016/j.acra.2005.05.027.
14. Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn. Reson. Med. 2010;64:457–471. doi: 10.1002/mrm.22428.
15. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58:1182–1195. doi: 10.1002/mrm.21391.
Figures