0568

A Multi-scale Deep ResNet for Radial MR Parameter Mapping
Zhiyang Fu1, Sagar Mandava1, Mahesh Bharath Keerthivasan1, Diego R Martin2, Maria I Altbach2, and Ali Bilgin1,2,3

1Electrical and Computer Engineering, University of Arizona, Tucson, AZ, United States, 2Department of Medical Imaging, University of Arizona, Tucson, AZ, United States, 3Biomedical Engineering, University of Arizona, Tucson, AZ, United States

Synopsis

Quantitative mapping of MR parameters has shown great potential for tissue characterization but long acquisition times required by conventional techniques limit their widespread adoption in the clinic. Recently, model-based compressive sensing (CS) reconstructions that produce accurate parameter maps from a limited amount of data have been proposed but these techniques require long reconstruction times making them impractical for routine clinical use. In this work, we propose a multi-scale deep ResNet for MR parameter mapping. Experimental results illustrate that the proposed method achieves reconstruction quality comparable to model-based CS approaches with orders of magnitude faster reconstruction times.

Introduction

Conventional MR parameter mapping techniques require long acquisition times. Recent model-based reconstruction methods1-5 enable accurate parameter mapping from a limited amount of data by utilizing compressed sensing (CS). However, these reconstructions are computationally demanding and necessitate long reconstruction times. Recently, deep neural networks have been proposed for medical image reconstruction problems6-10. In this work, we extend the use of deep neural networks to MR parameter mapping and introduce a multi-scale deep ResNet which yields high-quality parameter maps from undersampled data with very low reconstruction times.

Methods

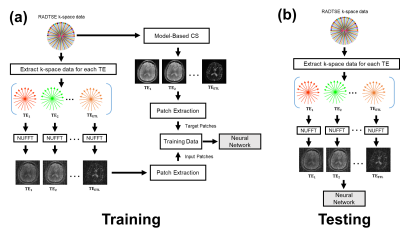
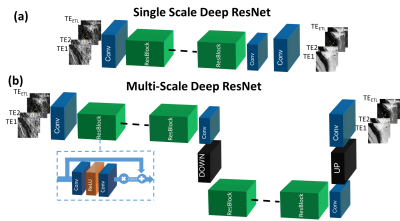
The proposed method was applied to T2 mapping with Radial Turbo-Spin-Echo (RADTSE)11 data acquisition. Fig.1(a) illustrates the supervised training procedure where RADTSE data is used to create multi-contrast images for both input and target. The input data was obtained by applying NUFFT12 to undersampled k-space at each echo time (TE) resulting in images with severe undersampling artifacts. The target data was obtained using model-based CS2,5. Note that if fully-sampled TE images can be acquired, they can be used as targets. However, such acquisitions are impractical in most parameter mapping applications. Unlike earlier deep neural network based image reconstruction methods which train on full images, the proposed network is trained on image patches. Patch-wise processing offers several advantages including requiring fewer training datasets, accelerated training, and low GPU memory requirement. The testing/deployment procedure is illustrated in Fig.1(b). Single-scale ResNet (SS-ResNet)13 (Fig.2(a)) and multi-scale ResNet (MS-ResNet) (Fig.2(b)) architectures were considered to test the hypothesis that a larger receptive field would be more capable of reducing global undersampling artifacts. All convolutional layers consisted of 3x3 kernels with 128 filters. The structure of the residual blocks is shown in Fig.2(b). Note that a residual scaling step with a constant scaling factor of 0.1 is used inside each residual block. In MS-ResNet, the down-sampling block uses convolution with stride=2 and the up-sampling block used the efficient sub-pixel convolution14. The networks were initialized randomly and trained using ADAM optimization with a learning rate of 1e-4. All networks were implemented in Torch15.

Data were acquired from 7 consenting subjects on a 1.5T Siemens Aera scanner using RADTSE on the abdomen with echo spacing= 6.0ms, ETL = 32, TR=1.8-2.3s, and 6 lines/TE with 256 readout points/line. Since fully sampled data was not available, model-based CS2,5 was used to generate the target images. 32x32 patches with stride=15 were extracted from the images and background patches were not included in training. Patches were normalized by subtracting the mean value of each echo across all training images and dividing by the corresponding standard deviation. For the abdomen experiment, three networks were trained: two SS-ResNets with 16 and 32 residual blocks, respectively, and an MS-ResNet with 32 residual blocks.

Data were also acquired from 5 consenting subjects on a 3T Siemens Skyra scanner using RADTSE on the brain with echo spacing= 9.0ms, ETL = 16, TR=5s. For each subject, a reference data (256 lines/TE) acquisition was followed by a separate undersampled data (16 lines/TE) acquisition. The reference and undersampled data were reconstructed using NUFFT. Patches were extracted and preprocessed in the same manner as the abdominal experiment. $$$l_2$$$ loss together with a total variation regularizer with weight=0.001 was used to train an MS-ResNet with 32 residual blocks. In both the abdomen and brain experiments, one subject was randomly selected for testing and the remaining subjects were used for training. T2 maps were calculated using the resulting TE images.

Results and Discussion

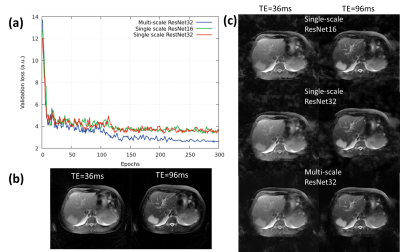
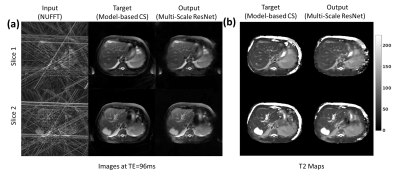
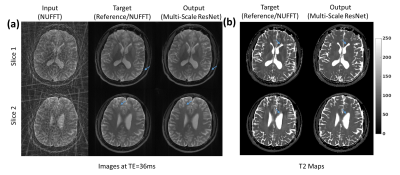
Fig.3 provides a comparison of the SS-ResNet and MS-ResNet. It can be seen that the MS-ResNet achieves lower validation loss as well as higher reconstruction quality compared to SS-ResNets. Fig.4 shows the reconstructed TE images and T2 maps in the abdomen. Note that the input images contain severe undersampling artifacts but the proposed network is able to remove these artifacts and produce TE images (and, thus, T2 maps) comparable to those obtained from the model-based CS method. Note that the model-based CS method requires a reconstruction time of roughly 45 min/slice whereas MS-ResNet requires roughly 0.35 s/slice for initial NUFFT reconstruction and 0.063 s/slice for network processing. Fig.5 shows results obtained using the brain datasets. It should be noted that the reference data contains motion artifacts due to the long acquisition time (~20 minutes) illustrating the impracticality of fully-sampled target data. In comparison, MS-ResNet yields high-quality TE images and T2 maps.

Conclusion

A multi-scale deep ResNet for MR parameter mapping was proposed. Results using in vivo brain and abdomen data showed that MS-ResNet can yield accurate TE images and T2 maps with reconstruction times several orders of magnitude faster than model-based CS methods.

Acknowledgements

The authors would like to acknowledge support from the Arizona Biomedical Research Commission (Grant ADHS14-082996) and the Technology and Research Initiative Fund (TRIF) Improving Health Initiative.

References

1. Doneva, M., Börnert, P., Eggers, H., Stehning, C., Sénégas, J., & Mertins, A. (2010). Compressed sensing reconstruction for magnetic resonance parameter mapping. Magnetic Resonance in Medicine, 64(4), 1114-1120.

2. Huang, C., Graff, C. G., Clarkson, E. W., Bilgin, A., & Altbach, M. I. (2012). T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magnetic resonance in medicine, 67(5), 1355-1366.

3. Zhao, B., Lu, W., Hitchens, T. K., Lam, F., Ho, C., & Liang, Z. P. (2015). Accelerated MR parameter mapping with low‐rank and sparsity constraints. Magnetic resonance in medicine, 74(2), 489-498.

4. Velikina, J. V., & Samsonov, A. A. (2015). Reconstruction of dynamic image series from undersampled MRI data using data‐driven model consistency condition (MOCCO). Magnetic resonance in medicine, 74(5), 1279-1290.

5. Tamir, J. I., Uecker, M., Chen, W., Lai, P., Alley, M. T., Vasanawala, S. S., & Lustig, M. (2017). T2 shuffling: Sharp, multicontrast, volumetric fast spin‐echo imaging. Magnetic resonance in medicine, 77(1), 180-195.

6. Schlemper, J., Caballero, J., Hajnal, J. V., Price, A., & Rueckert, D. (2017, June). A Deep Cascade of Convolutional Neural Networks for MR Image Reconstruction. In International Conference on Information Processing in Medical Imaging (pp. 647-658). Springer, Cham.

7. Knoll F., Hammernik K., Garwood E., Hirschmann A., Rybak L., Bruno M., Block T., Babb J., Pock T., Sodickson D. K., & Recht M. P. Accelerated knee imaging using a deep learning based reconstruction, Proc. of ISMRM, 2017.

8. Han Y. S., Lee D., Yoo J, & Ye J. C. Accelerated Projection Reconstruction MR imaging using Deep Residual Learning, Proc. of ISMRM, 2017.

9. Hammernik K., Knoll F., Sodickson D. K., & Pock T. L2 or not L2: Impact of Loss Function Design for Deep Learning MRI Reconstruction, Proc. of ISMRM, 2017.

10. Jin, K. H., McCann, M. T., Froustey, E., & Unser, M. (2017). Deep convolutional neural network for inverse problems in imaging. IEEE Transactions on Image Processing, 26(9), 4509-4522.

11. Altbach, M. I., Outwater, E. K., Trouard, T. P., Krupinski, E. A., Theilmann, R. J., Stopeck, A. T., ... & Gmitro, A. F. (2002). Radial fast spin‐echo method for T2‐weighted imaging and T2 mapping of the liver. Journal of Magnetic Resonance Imaging, 16(2), 179-189.

12. web.eecs.umich.edu/~fessler/irt

13. He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).

14. Lim, B., Son, S., Kim, H., Nah, S., & Lee, K. M. (2017, July). Enhanced deep residual networks for single image super-resolution. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops.

15. http://torch.ch/

Figures

Figure 1. (a) The proposed training strategy involves creation of input and target patches from training data. For input data, undersampled k-space data at each TE is processed using NUFFT. For target data, the RADTSE dataset is processed using a model-based CS technique. Patches are extracted from the resulting images and used for supervised learning. (b) For testing/deployment, undersampled k-space data at each TE is processed using NUFFT. These multi-constrast images contain severe undersampling artifacts. Note that during the testing phase patch extraction is unnecessary since the convolutional kernels can be applied directly to the images.

Figure 2. Network architectures. (a) Single scale deep ResNet. Stacked residual blocks are placed in between input and output convolutional layers. (b) Multi-scale deep ResNet. The network processes data at multiple spatial scales. The down-sampling layer uses a stride-2 convolution and the up-sampling layer uses the efficient sub-pixel convolution. The structure of ResBlock is shown in the dashed blue box.

Figure 3. Comparison of Single-scale and Multi-scale ResNets with different number of residual blocks. Single-scale ResNet32 has the same number of residual blocks as Multi-scale ResNet32. l2 loss was used during training for all networks. (a) Validation loss on testing patches over epochs for the three networks. Note the lower validation loss achieved by Multi-scale ResNet32. (b) Reference reconstructions (from model-based CS) for two TE images corresponding to 67X acceleration with respect to Nyquist rate (6 lines/TE). (c) The corresponding outputs from three networks. Note that the quality of the Multi-scale ResNet reconstruction is comparable to model-based CS reconstructions.

Figure 4. Test results on abdominal data. l1 loss together with a total variation regularizer of weight=0.001 was used during training. (a)TE images at 96ms obtained using NUFFT, Model-based CS, and Multi-scale ResNet which constitute the input, target, and output images, respectively, of the proposed network. (b) T2 maps obtained by Model-based CS and Multi-scale ResNet.

Figure 5. Test results on brain data. (a) TE images at 36ms obtained using NUFFT on the undersampled data (16 lines/TE), NUFFT on the reference data (256 lines/TE), and Multi-scale ResNet using the undersampled data (16 lines/TE). (b) T2 maps of network target and output. Note that the long acquisition time (~20 min) needed for the reference data resulted in motion artifacts in the target image. These artifacts were eliminated in the Multi-scale ResNet reconstructions.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0568