0543

Multi-receiver coil combination for breast phase-based Electrical Property Tomography Using B1- estimation
Jun-Hyeong Kim1, Jaewook Shin1, Soo-Yeon Kim2, and Dong-Hyun Kim1

1electrical electronic engineering, Yonsei University, seoul, Republic of Korea, 2Department of Radiology, Seoul National University Hospital, Seoul, Republic of Korea

Synopsis

Phase-based EPT assumes the spatial homogeneity of both B1+ and B1- magnitude. However, when it comes to multi-receivers is used for improved SNR, the assumption becomes invalid especially for B1-. To overcome this problem, a subject-specific multi-Rx combination method was suggested [2]. However, this method can give a solution that is biased by the transmit field (B1+) when it is inhomogeneous. In this study, an alternative multi-Rx combination method is proposed. B1- is estimated from multi-receiver images by solving an inverse problem. Afterwards, optimal coil-coefficients for combination are calculated using the estimated B1- field. The method is applied to in-vivo breast conductivity imaging.

Introduction

Phase-based EPT is a technique to reconstruct tissue electrical property using only transceive phase[1]. This technique assumes the spatial homogeneity of both B1+ and B1- magnitude. However, when it comes to multi-receivers is used for improved SNR, the assumption becomes invalid especially for B1-[2]. To overcome this problem, a subject-specific multi-Rx combination method was suggested [2]. However, this method can give a solution that is biased by the transmit field when it is inhomogeneous. In this study, an alternative multi-Rx combination method is proposed. B1- is estimated from multi-receiver images by solving an inverse problem. Afterwards, optimal coil-coefficients for combination are calculated using the estimated B1- field. The method is applied to in-vivo breast conductivity imaging.

Theory

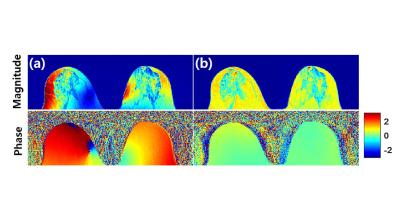
Figure 1 shows image combined using a simple ‘complex sum’ and the aforementioned subject-specific method(aka magnitude least squares(MLS) method)[2]. As in Fig.1a, the simple ‘complex-sum’ cannot flatten the image due to inhomogeneity of B1-. To overcome this problem, MLS-optimization was previously applied to multi-Rx combination [2]. (Fig.1b) However, when the magnitude of B1+ is inhomogeneous, even MLS-method can suffer from inhomogeneity. Specifically, magnitude of combined B1- would be inversely proportional to magnitude of B+ field over each homogeneous ROI.(Icommon=constant, Eq.1) $$ S_{comb} = I_{common}\cdot \mid B^+_1 \mid\mid B^-_{comb} \mid=1 \space\space\space\Rightarrow \space\mid B^-_{comb} \mid= \frac{1}{ I_{common}\cdot \mid B^+_1 \mid} (Eq.1) $$ To overcome the B1+ magnitude bias in MLS-method, MLS-optimization problem should be solved in B1-, not in received image. B1- field can be estimated by solving a log-linear inversion problem. Using Eq.2, log B1- field for each coil can be calculated. $$ log\mid S_{PD,j} \mid=log\mid PD_{w}\cdot B^+_1 \mid + log\mid B^-_{1,j} \mid , \space \space log\mid S_{T2,j} \mid=log\mid T2_{w}\cdot B^+_1 \mid + log\mid B^-_{1,j} \mid (Eq.2) $$ After B1- field was estimated, the coil-coefficients needed to yield a homogeneous B1- field is determined by Eq.3.

$$ \left\{c_j\right\}=argmin_{c_j}\left\{ \sum_{(x,y,z)\in ROI }\parallel \sum_{j }B^-_{1,j}(x,y,z)-1 \parallel ^2_2 +\lambda \sum_j \mid c_j \mid^2 \right\} (Eq.3) $$

Methods

1. Data Acquisition : In-vivo breast imaging experiments were conducted using a 3T clinical scanner (Skyra;Siemens,Erlangen,Germany), breast 18 channel-coil. TSE sequence was acquired : PDw 3.2-mm thickness, image size=384×260, FOV=320×320mm, TR=10800ms, TEeff=6ms, ETL=20, number of slice=45. In addition, a separate T2-weighted image (TE=101ms) was acquired. Total scan time ~5min. This study was approved by our Institutional Review Board (IRB).

2. Coil-combination using fat mask vs coil-combination with B1- estimation

Previous method(Homogenize magnitude of combined image over fat-masked region) :

a) Fat-mask was selected based on the intensity of T2-weighted image (12%thresholding).

b) The received image was implemented to MLS-optimization problem which yields the coil-coefficients: [2].

c) All coil images were complex-summed after multiplying with the acquired coil-coefficients.

Proposed Method(Homogenize magnitude of combined B1- over whole breast region) :

a) To estimate B1-, a log-linear inversion problem was solved. Using Eq.3, log B1- field for each coil was calculated.

b) The estimated B1- field was implemented into Eq.3 which yields the coil-coefficients:

c) All coil images were complex-summed after multiplying with the acquired coil-coefficients.

3. EPT reconstruction : A 3D-weighted polynomial fitting was performed[2].(maximum kernel size=1.75x2.5x3.2cm2) For magnitude weighting factor, both method using magnitude of combined image from MSL-method.

Result

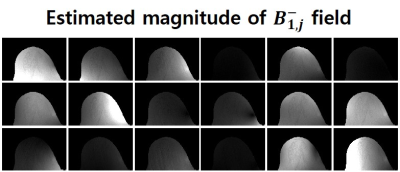
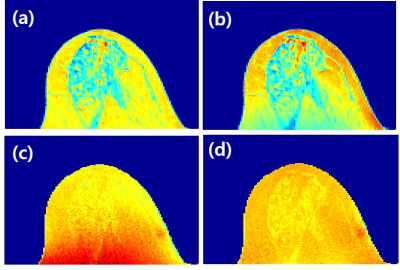
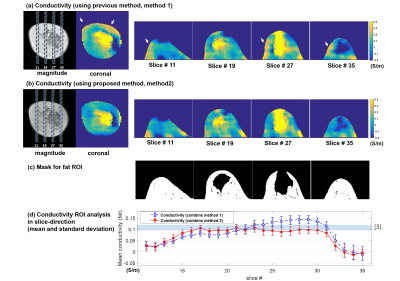
Figure 2 shows estimated magnitude of B1- field. Figure 3 shows magnitude of combined image(a,b) and combined B1-(c,d) for using both method 1 and 2. Magnitude of image using previous method Fig3.a give homogeneous intensity, but it’s estimated B1- field Fig3.c is not homogeneous. However, B1- field of proposed method Fig3.d is homogeneous. Combined image from previous method will contain the error from B1+ inhomogeneity as expected in Eq.1. Figure 4 shows the result of phase-based EPT with the two multi-Rx combination methods. To evaluate the conductivity maps of method 1 and 2, the mean and standard deviation of fat-ROI conductivity was calculated. To emphasize conductivity value of fat, colorbar was selected to encoded green around 0.1S/m because conductivity value of mammary at 100Mhz has been reported to be around 0.11S/m[3]. Boxes in the coronal magnitude image indicate locations of axial conductivity map. Arrows in conductivity map in Fig.4a indicate error region which is reduced in Fig.4b.

Discussion

To guarantee the accuracy of conductivity map, homogeneity of transmit and receive B1 field is essential. In practice however, it is hard to acquire a homogeneous magnitude of the B1+ without using multi-transmit system. To reduce the error-propagation from magnitude of B1+ inhomogeneity, B1- should be extracted exactly. In this study, PD and T2 weighting images were used to extract the magnitude of B1-. But, these two images may not necessary to estimate B1-, B1- estimation using single image for coil combine should be studied in future work.

Acknowledgements

This research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Science, ICT and future Planning (NRF-2015R1A2A1A15052174)

References

1. T. Voigt. et al., Quantitative conductivity and permittivity imaging of the human brain using electrical properties tomography. Mag. Reson. Med., Vol 66(2), August 2011, Pages 456-466.

2. Joonsung Lee, et al., MR_Based Conductivity Imaging Using Multiple Receiver Coils. Magn Reson Med. Volume 76, Issue 2, August 2016, Pages 530–539

3. W. T. Joines et al., The measured electrical properties of normal and malignant human tissues from 50 to 900 MHz. Medical Physics 21, 547 (1994)

Figures

Figure 1. (a) Complex sum of received coil images. (b) Multi-receiver combined image using magnitude of fat mask region.

Figure 2. Magnitude of estimated B1- field.

Figure 3. (a) is magnitude of combined image using previous method (b) is magnitude of combined image using proposed method (c) is magnitude of B1- combined with coil-coefficient of previous method. (d) is magnitude of B1- combined with coil-coefficient of proposed method.

Figure 4. first column of (a), (b) is magnitude of combined signal. (a) is conductivity value which is calculated from Previous method 1 (using fat mask ROI). (b) is conductivity value which is calculated from Proposed method 2. (c) is fat mask for calculating mean and standard deviation of conductivity value of fat region. (d) is line plot of mean conductivity and standard deviation of fat

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0543