0541
Robust Fat-water Separation using Binary Decision Tree Algorithm1Huazhong University of Science and Technology, Wuhan, China, 2Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences, Shen Zhen, China, 3University of Chinese Academy of Sciences, Beijing, China
Synopsis
Purpose: To propose an robust fat water separation method using binary decision tree algorithm.
Methods: In this paper, a novel fat-water separation algorithm using binary decision tree is proposed. Pixels are firstly clustered into sub-regions. Different from existing region growing algorithms, the proposed method solves the phasor ambiguity problem region by region. The method was tested on data sets from ISMRM 2012 Challenge.
Results:Fat-water separation were successfully achieved by the proposed method in the datasets.
Conclusion: A novel method using binary decision tree algorithm is proposed for robust and accurate water-fat separation.
Introduction
Chemical shift encoded fat-water imaging in MRI is of great significance in clinical applications such as fatty liver diseases 1. Various methods have been proposed to solve the ambiguity between fat and water 2-4, however, these methods may run into difficulty when dealing with areas with fast field change and spatially isolated objects. In this paper, a novel algorithm using binary decision tree is proposed. In this method, pixels are firstly clustered into sub-regions. Instead of determining the solutions pixel by pixel as in the region growing algorithm 4, the algorithm solves the problem in unit of sub-regions through a binary decision tree, thus simplifying the problem into a low dimensional binary decision problem.Theory
Introducing the definition of ‘phasor’ 2, the globally optimal phasor solution($$$P_G$$$) for one pixel can be obtained through one dimensional search 3 . Let the swapped solution of $$$P_G$$$ be $$$\overline{P_G}$$$. Define $$$P_w$$$ is either $$$P_G$$$ or $$$\overline{P_G}$$$, of which the corresponding separation results in $$$|ρ_w |$$$ > $$$|ρ_f |$$$, while $$$P_f$$$ as that $$$|ρ_f |$$$ > $$$|ρ_w |$$$. The two candidate phasor solutions are classified into two groups, namely, $$$P_w$$$ and $$$P_f$$$.
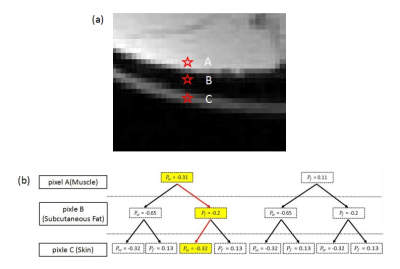
Figure 1 shows the principle of decision tree algorithm. The red starts in Fig. 1(a) represents three adjacent pixels in different tissues. There are two possible phasor solutions for each pixel, making there are 8 solution combinations for the three pixels. Fig. 1(b) aligns the eight combinations in a tree form according to the binary choice of $$$P_w$$$ or $$$P_f$$$ for each pixel. Among all combinations , the combination that is marked in yellow has the least phasor change through the tree paths (marked in red). The phasor solutions, along with the identification of fat and water for the three pixels are therefore decided.
Applying the decision tree to whole image pixel by pixel would be computationally intensive as there might be $$$2^N$$$ phasor solution combinations for N pixels. Therefore, neighboring pixels that have both similar $$$P_w$$$ and $$$P_f$$$ are firstly clustered as one region. As a result, the whole image is partitioned into several sub-regions (usually 20-50). Note that pixels inside each sub-regions have consistent choices of phasor solutions, either all from $$$P_w$$$ or all from $$$P_f$$$. The decision tree is then applied to the sub-regions to make the algorithm computationally feasible.
Materials and methods
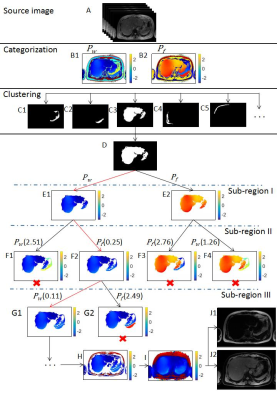
The flowchart of whole algorithm is illustrated in Figure 2. The algorithm starts with finding phasor candidates $$$P_G$$$ and $$$\overline{P_G}$$$ for each pixel. Phasor candidates are categorized into $$$P_w$$$ and $$$P_f$$$, as shown in Fig 2 (B1-B2). The whole image is then partitioned into several sub-regions (Fig 2C). The decision tree is organized as follows: decision tree starts from the biggest sub-region (Fig 2D) as root node and traverse all other sub-regions according to the spatial proximity to the parent one. In each level of the tree, the nodes are partitioned into two paths, corresponding to two possible solutions, either from $$$P_w$$$ or $$$P_f$$$ for the next sub-region. The cost function of the tree path, given in the brackets, is defined as absolute phasor difference between the neighboring pixels of these two sub-regions. When the cost function of one node is larger than a predefined threshold(here is 1 in the example), which means there is an abrupt phasor change between the sub-regions, implying that the phasor choice is not appropriate. The tree traverse then terminates at these nodes, as shown in Fig. 2 (F2-F4, G2, marked with red crosses). The traverse path reaches the last sub-region indicates the final phasor solution for each sub-regions is identified(Fig 2H). Using Fig 2H as seedmap, the field map(Fig 2I) can be obtained using region-growing algorithm 5, the recognition(either fat or water) for the whole image is obtained(as shown in Fig 2 (J1-J2)).Results
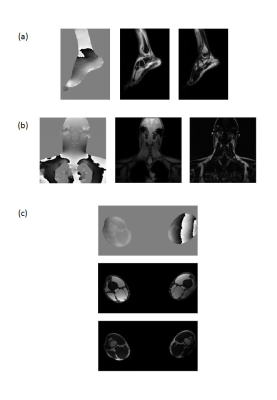
The method was tested on the datasets from ISMRM 2012 Challenge. Fat-water separation were successfully achieved by the proposed method in these data sets. No apparent swap was observed. Fat-water separation results of ankle, c-spine and thighs are shown in Fig 3(a), (b) and (c) respectively. The algorithm is proven to work well in spatially disjoint objects and areas with fast field change.Discussion and conclusions
A novel method using binary decision tree algorithm is proposed for robust and accurate water-fat separation. Different from existing region growing algorithms, the proposed method solves phasor ambiguity problem region by region after pixel clustering, lowering the dimension of binary problem significantly. Predefined cost function threshold was used to terminate tree traverse path, simplifying the tree path finding. Accurate and robust separation results were achieved in all the data tested.Acknowledgements
No acknowledgement found.References
1. Reeder SB, Cruite I, Hamiton G Sirlin CB. Quantitative assessment of liver fat with magnetic resonance imaging and spectroscopy. J Magn Reson Imaging 2011;34:729-749;
2. Qing-San Xiang. Two-point water-fat imaging with partially-opposed-phase(POP) Acquisition: an asymmetric Dixon method. Magn Reson Med 2006;56:572-584;
3. D.Hernando, J.P.Haldar, B.P.Sutton, J.Ma, P.Kellman, Z.-P. Liang. Jiont estimation of water/fat images and field inhomogeneity map. Magn Reson Med 2008; 59:571-580;
4. Wenmiao Lu, Brian A.Hargreaves. Mulitresolution field map estimation using golden section search for water-fat separation. Magn Reson Med 2008;60:236-244;
5. Chuanli Cheng, Chao Zou, Changhong Liang, Xin Liu, Hairong Zheng. Fat-water separation using a region-growing algorithm with self-feeding phasor estimation. Magn Reson Med 2017;77:2390-2401.
Figures