0495

The effects of diffusion on the tissue orientation dependent gradient echo dynamic susceptibility contrast signal

Jonathan Doucette^1,2, Enedino Hernández-Torres^1,3, Christian Kames^1,2, Luxi Wei⁴, and Alexander Rauscher^1,3,5

¹UBC MRI Research Centre, University of British Columbia, Vancouver, BC, Canada, ²Physics and Astronomy, University of British Columbia, Vancouver, BC, Canada, ³Pediatrics, University of British Columbia, Vancouver, BC, Canada, ⁴Department of Medical Biophysics, University of Toronto, Toronto, ON, Canada, ⁵Division of Neurology, Faculty of Medicine, University of British Columbia, Vancouver, BC, Canada

Synopsis

Gradient echo dynamic susceptibility contrast (DSC) imaging of cerebral white matter tissue perfusion exhibits a strong dependency on the angle between white matter fibres and the main magnetic field. Here, we investigate the extent to which the diffusion of spins within the locally magnetically inhomogenous environment affects the orientation dependency of the DSC signal using a numerical model of the transverse magnetization within a voxel containing both isotropic and anisotropic vasculature. We found that diffusion increases the measured change in $$$R_2^*$$$ by up to an average of 3.2% for typical diffusion values, independent of fibre orientation, and further improves the fit between the simulated and measured $$$R_2^*$$$ values.

Introduction

Perfusion in cerebral white matter tissue as measured by gradient echo dynamic susceptibility contrast (DSC) imaging is known to exhibit a strong dependency on the angle between the white matter (WM) fibre and the main magnetic field $$$B_0$$$¹. This effect is due to large anisoptropic vasculature running in parallel with the WM tracts, which introduces orientation dependent magnetic field inhomogeneities that are superimposed on top of orientation independent field inhomogeneities due to isotropic vasculature. This results in the measured change in $$$T_2^*$$$ during a DSC experiment to depend on the angle between the WM tract and $$$B_0$$$, as well as the contrast agent (CA) concentration. In particular, field inhomogeneities near large anisotropic vessels increase with increasing fibre angle and increasing CA. This causes a large orientation effect in measured $$$\Delta{R_2^*}$$$ values, on the order of 100%¹.

While a model based on static dephasing fits the measured data well, diffusion of spins within the static magnetic field inhomogeneities introduces further signal loss. This is due to spins being exposed to larger field inhomogeneities in the vicinity of blood vessels by means of diffusion, effectively extending the range of the inhomogeneities; this effect is further increased by the CA. The orientation dependency of the signal loss due to diffusion depends on the relative amount of isotropic vs. anisotropic vasculature; diffusive signal loss near smaller vessels is larger due to higher field gradients, and thus the isotropic losses can dominate. Here, we investigate the extent to which diffusion impacts the measured $$$\Delta{R_2^*}$$$ value as a function of WM fibre orientation in GRE-DSC through an extension of a previously developed numerical model of diffusion within a magnetically inhomogeneous environment consisting of a vascular bed with both isotropic and anisotropic components³.

Methods

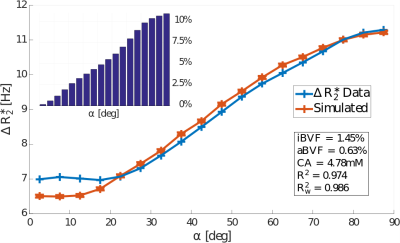
Data from 13 subjects with multiple sclerosis was acquired at 3T¹. DSC was acquired with gradient echo EPI (TR/TE=2417ms/40ms, voxel volume=1.5x1.5x4$$${mm}^3$$$). Fibre angle was calculated using a DTI scan as described in². The DSC signal in each WM voxel was sorted according to fibre angle $$$\alpha$$$ into bins of width $$$5^\circ$$$ ranging from $$$2.5^\circ$$$ to $$$87.5^\circ$$$. $$$\Delta{R_2^*}=-\frac{1}{TE}\log(\frac{S}{S_0})$$$ was calculated and averaged across all voxels in each bin for all subjects. $$${S_0}$$$ is the baseline signal, and $$${S}$$$ is the signal corresponding to peak CA. Figure 1 shows the resulting $$$\Delta{R_2^*}$$$ vs. $$$\alpha$$$ curve, as well as the distribution of voxels with respect to fibre angle.

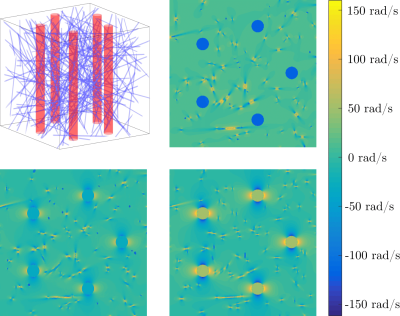
Simulation of the transverse magnetization occurs within a voxel filled with anisotropic and isotropic blood vessels. The construction of the voxel geometry and subsequent calculation of field inhomogeneities is described in³. An example voxel and corresponding field inhomogeneity cross-sections are shown in Figure 2. Within this geometry, the transverse magnetization is propagated forward in time by solving the Bloch-Torrey equation $$$\frac{dM}{dt}=D{\nabla^2}M-(R_2(\vec{r})+i\omega(\vec{r}))M$$$ up until the echotime TE=40ms³.The simulation contains three free parameters which are varied in order to best reproduce the measured $$$\Delta{R_2^*}$$$ vs. $$$\alpha$$$ curve: the isotropic blood volume fraction iBVF of the small isotropic vessels, the anisotropic blood volume fraction aBVF of the large anisotropic vessels, and the peak contrast agent concentration CA. These three parameters were optimised using weighted least squares regression with MATLAB's lsqnonlin function, where the weights were taken to be the number of data points in each angle bin in order to account for the angular distribution of the WM fibres (Figure 1). Additionally, the diffusion constant and number of large vessels simulated were varied in discrete steps.

Results

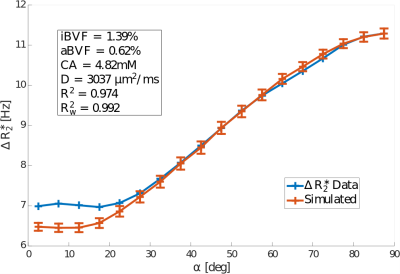
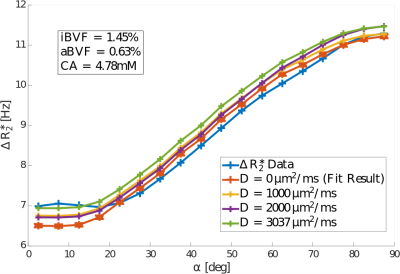
Diffusion was found to increase the modelled $$$\Delta{R_2^*}$$$ value by up to 0.22Hz, 0.25Hz, and 0.39Hz for diffusion constants of $$$1mm^2/s$$$, $$$2mm^2/s$$$, and $$$3.037mm^2/s$$$³, respectively, independent of fibre orientation (Figure 4). The corresponding weighted average increases in $$$\Delta{R_2^*}$$$ were 1.4%, 1.9%, and 3.2%. Optimal model fits were obtained for N=4 anisotropic vessels. The inclusion of diffusion improved the model fit, with the weighted coefficient of determination $$$R^2_w$$$ increasing from 0.986 to 0.992 (Figure 3).

Discussion and Conclusion

Diffusion was found to increase the simulated $$$\Delta{R_2^*}$$$ value approximately independent of the orientation of the WM fibre with respect to $$$B_0$$$, suggesting that diffusive signal loss is dominated by isotropic vasculature as opposed to anisotropic vasculature for GRE-DSC scans. This finding agrees well with the optimised parameter values of iBVF=1.39% and aBVF=0.62%, indicating that approximately two-thirds of WM vasculature is contained in the isotropic vessels. A total blood volume fraction of 2.01% was found, which agrees well with literature values.

Additionally, including diffusion increased the weighted coefficient of determination $$$R^2_w$$$ of the model. This suggests that diffusion plays a small, but not insignificant role in GRE-DSC imaging compared to static dephasing alone. However, the parameters computed with the extended model are very similar to the static dephasing model.

Acknowledgements

No acknowledgement found.

References

1. Hernández-Torres E, Kassner N, Forkert ND, Wei L, Wiggermann V, Daemen M, Machan L, Traboulsee A, Li D, Rauscher A. Anisotropic cerebral vascular architecture causes orientation dependency in cerebral blood flow and volume measured with dynamic susceptibility contrast magnetic resonance imaging. J Cereb Blood Flow Metab. 2016

2. Hernández-Torres E, Wiggermann V, Hametner S, et al. Orientation dependent MR signal decay differentiates between people with MS, their asymptomatic siblings and unrelated healthy controls. PLoS One 2015; 10: e014095

3. Jonathan Doucette, Luxi Wei, Christian Kames, et al. Anisotropic cerebral vascular architecture causes orientation dependency in cerebral blood flow and volume measured with spin echo dynamic susceptibility contrast magnetic resonance imaging. Proceedings of the International Society of Magnetic Resonance and Medicine 25, Honolulu, Hawaii, USA.

Figures

Optimised $$$\Delta{R_2^*}$$$ vs. $$$\alpha$$$ curve without diffusion. The distribution of voxels with angle $$$\alpha$$$ is shown in the top left. The asymmetry in the angular distribution of the WM fibres is due to the fact that for uniformly randomly distributed unit vectors on a sphere, there are fewer vectors pointing nearly parallel with the z-axis than there are vectors with larger angles to the z-axis. For this reason, there are fewer data points for smaller WM fibre angles than there are for larger angles. Minimization procedures account for this fact by weighting the squared errors at each angle by the corresponding number of data points.

The top-left figure shows an example voxel geometry (isotropic voxel, N=5 anisotropic vessels). The magnetic field generated by this configuration is computed by convolving the susceptibility map with the dipole kernel³. Cross-sections of the frequency shift map ω are shown for α=0°(top right), 45°(bottom left), and 90°(bottom right). Near large vessels, the frequency shift remains relatively constant compared to the frequency shift near small vessels, which changes rapidly over short distances. For this reason, signal loss due to diffusion is larger in the vicinity of small vessels. Note the increase in strength and range of inhomogeneities around the large anisotropic vessels as α increases.

Optimised $$$\Delta{R_2^*}$$$ vs. $$$\alpha$$$ curve with diffusion. The weighted coefficient of determination $$$R^2_w$$$ is increased relative to the case with no diffusion, while the simulation parameters have remained relatively constant.

Comparison of $$$\Delta{R_2^*}$$$ vs. $$$\alpha$$$ for varying diffusion constants, using the optimised fit parameters from the $$$D=0{\mu}m^2/ms$$$ simulations. Note the approximately uniform increase in $$$\Delta{R_2^*}$$$ across all angles compared to the baseline $$$D=0{\mu}m^2/ms$$$ case.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

0495