0481
Off k-space center and spin-history artifacts Self-Navigator Intelligent Filter (SNIF) for quasi-random 3D-radial acquisitions1Laboratoire d'Imagerie par Résonance Magnétique Médicale et Multi-Modalités (IR4M), Université Paris-Sud, Orsay, France, 2Université Paris-Saclay, Orsay, France, 3CNRS, Orsay, France, 4Applications & Workflow, GE Healthcare, Orsay, France, 5Department of Radiology and Biomedical Imaging, University of California San Francisco, San Francisco, CA, United States
Synopsis
For 3D radial acquisitions featuring a quasi-random order of spoke orientations in k-space, implementable in UTE pulse sequences, respiratory and cardiac self-navigators are usually extracted from the assumed k-space center thanks to standard bandpass filters to perform self-gating. To remove more efficiently the background noise, SNIF, Self-Navigator Intelligent Filter, takes into account the underlying physics of the MR acquisition to filter out of the DC signal both off k-space center and spin-history effects. SNIF systematically enhances both respiratory and cardiac self-navigators. It even sometimes reveals their spectral first harmonics, which remained otherwise buried into the background noise.
Introduction
Radial MR acquisitions offer a set of advantages like ultrashort TE (UTE)1, robustness to under-sampling2 and embedded respiratory and cardiac motion information. This facility, called self-navigation, typically consists in extracting the motion-related modulations of the DC signal, expectedly measured at the supposed center of the k-space3,4. Usually, when pseudo-random 3D radial sampling is implemented (following either a golden ratio5 or a randomized order of spokes6), this extraction is performed by applying bandpass filters tuned around the physiological frequencies7, which leaves the noise contained in those frequency bands. In this study, we propose SNIF, an intelligent filtering method, which assumes that the DC signal is generally:
- acquired slightly off the actual k-space center, and
- the cumulative result of the previous repetitions.
Theory
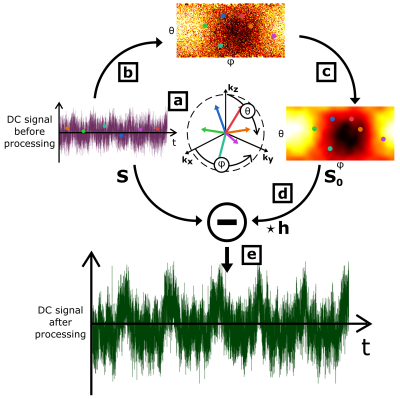
Let S0 be the assumed DC signal acquired on a motionless object. Because of technical imperfections, S0 is never experimentally measured at the exact center of k-space. Moreover, in general, this measured signal depends on transverse magnetization states of previous TR periods. This spin-history effect, combined with the off k-space center effect, can be modeled by a convolution kernel h = [aN … a3 a2 a1 1], where N is the number of preceding weighting repetitions, such that the DC signal is a sum of the back-shifted and re-weighted S0 signal S0⋆h. If the object is animated by a low-amplitude motion with a characteristic period T >> TR, the DC signal can be modeled as S = Sm + S0⋆h, where Sm is the self-navigator signal. For k-space quasi-random off-centered radial sampling, S0 can be considered as white noise with respect to Sm. In this case, the DC signal autocorrelation, A(S), can be expressed as the sum of a slowly-varying, ASlow, and off k-space center and spin-history components: A(S) = λASlow + (1-λ)h⋆h.Methods
Thoracic MR acquisitions were performed on a GE Signa PET/MR 3.0 T scanner on one healthy human volunteer breathing freely, equipped with a 30-channel thoracic coil for signal reception, an abdominal belt and a PPG sensor to record the temporal features of respiratory and cardiac motions. A 3D radial (kooshball) UTE sequence with a random order of spoke orientations was implemented with TE / TR = 100 µs / 2 ms, FOV = (32×32×22.4) cm3, voxel size = (1.3×1.3×1.3) mm3, RF spoiling, ramp-sampling and no under-sampling. It resulted in an acquisition of 150,806 spokes for a total scan time of 5 min 2 s.
MR data set were processed to extract the off k-space center effect S0 from S (see Figure 1), and the convolution kernel h was iteratively computed from A(S). Sm was then estimated by calculating S - S0⋆h. S was defined as the absolute value of the first acquisition point of each spoke for a given reception channel, and the analysis was carried separately on each channel. To correct the spin-history effect, 20 components were considered for h (h = [a20 … a1 1]).
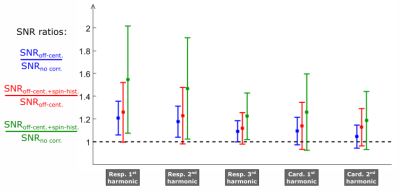
The efficiency of SNIF was evaluated on the SNR of the first three and first two harmonics of the respiratory and cardiac self-navigators, respectively. The reference motion frequencies were set with the abdominal belt and PPG traces. The SNR was inferred at each of these frequencies from the ratio between the amplitude of local Gaussian fits with the amount of background noise, provided by a linear regression.
Results
Figure 2 shows the spectra of the self-navigators obtained before and after the application of SNIF for one of the 30 reception channels. Figure 3 shows an overview of the efficiency of SNIF on all channels.Discussion
On Figure 2, after applying SNIF, we observe both the global energy conservation for each motion harmonic and the decrease of the background noise around each peak. Some motion harmonics, buried into the noise before correction (magenta data points), are revealed by SNIF (green data points). SNIF extracts motion information from off-center and spin-history noise. On Figure 3, we see that each correction step in SNIF increases the SNR of each harmonic for almost every channel (standard deviation bars above 1).
The direct measurement of off-center and spin-history effects from data makes SNIF universal for every 3D radial sequence, whatever acquisition parameters are selected. In an ideal situation where S0 is uniform and h is a Dirac, SNIF does not alter the DC signal.
Conclusion
This study shows the great potential of SNIF: by modelling the physics underlying the measurement during a quasi-random 3D-radial acquisition, we are able to efficiently extract respiratory and cardiac self-navigators out of the noise, which partly results from off k-space center and spin-history artifacts.Acknowledgements
PET/MR platform affiliated to the France Life Imaging network (grant ANR-11-INBS-0006).References
1 P. D. Gatehouse and G. M. Bydder, “Magnetic Resonance Imaging of Short T2 Components in Tissue”, Clin. Radiol., vol. 58, no. 1, pp. 1–19, Jan. 2003.
2 R. W. Chan, E. A. Ramsay, E. Y. Cheung, and D. B. Plewes, “The influence of radial undersampling schemes on compressed sensing reconstruction in breast MRI”, Magn. Reson. Med., vol. 67, no. 2, pp. 363–377, Feb. 2012.
3 M. Tibiletti, A. Bianchi, Å. Kjørstad, S. Wundrak, D. Stiller, and V. Rasche, “Respiratory self-gated 3DUTE for lung imaging in small animal MRI”, Magn. Reson. Med., vol. 78, no. 2, pp. 739–745, Aug. 2017.
4 N. S. Higano et al., “Retrospective respiratory self-gating and removal of bulk motion in pulmonary UTE MRI of neonates and adults”, Magn. Reson. Med., vol. 77, no. 3, pp. 1284–1295, Mar. 2017.
5 L. Feng et al., “XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing”, Magn. Reson. Med., vol. 75, no. 2, pp. 775–788, Feb. 2016.
6 W. Jiang et al., “Motion robust high resolution 3D free-breathing pulmonary MRI using dynamic 3D image self-navigator”, Magn. Reson. Med., Oct. 2017.
7 J. Liu, P. Spincemaille, N. C. F. Codella, T. D. Nguyen, M. R. Prince, and Y. Wang, “Respiratory and cardiac self-gated free-breathing cardiac CINE imaging with multiecho 3D hybrid radial SSFP acquisition”, Magn. Reson. Med., vol. 63, no. 5, pp. 1230–1237, May 2010.
Figures