0479
Improved subsampling trajectory for reliable assessment of cardiac and respiratory motion in 5D MRI for body motion correction1Section on Experimental Radiology, University Hospital of Tuebingen, Tuebingen, Germany, 2Institute of Signal Processing and System Theory, University of Stuttgart, Stuttgart, Germany, 3Department of Radiology, University Hospital of Tuebingen, Tuebingen, Germany
Synopsis
Respiratory and cardiac motion may cause artifacts in body trunk imaging if patients cannot hold their breath or triggered acquisitions are not practical. Retrospective correction strategies cope with motion by fast sequences under free-movement conditions. In the acquisition, a random subsampling with global variable-density scaling is usually applied. Improved sampling efficiency in terms of acquired SNR per sample can be achieved if the underlying energy distribution is considered. An image upscaling via dictionary learning from the localizer with extraction of the energy distribution and local shaping of the hybrid Cartesian subsampling improves the overall image quality and SNR by 45%.
Introduction
Motion is the main extrinsic source for image artifacts in thoracic and abdominal MRI which can strongly deteriorate image quality and thus diagnostic accuracy. Motion correction (MC) may help to reduce or image these artifacts which mainly originate from periodic respiratory and cardiac motion. The acquired data itself can then be corrected or movement information can be extracted and applied to other imaging modality for MC, e.g. PET/MR MC1. An MC application demands high spatial and temporal resolution under free-movement conditions which in turn requires fast acquisition strategies. Compressed Sensing (CS) provides one way of achieving this and its subsampling concept can be smoothly adapted for this dynamic imaging purpose.
The proposed methods differ in the applied subsampling scheme and k-space trajectory. Non-Cartesian approaches2,3 might intrinsically show a better image quality for moving objects than Cartesian trajectories, because of low-frequency oversampling. However, non-Cartesian readouts have a reduced sampling efficiency, require quadratic FOVs and a regridding in the reconstruction. Hybrid methods4-7 combine non-Cartesian trajectories with Cartesian readouts to utilize the best of both approaches.
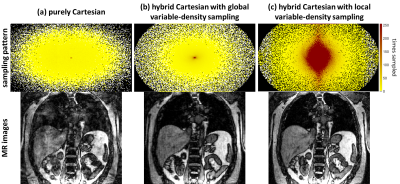
The trajectories determine the applied subsampling mask. For Cartesian or hybrid Cartesian methods, a global variable-density subsampling is usually applied to control the sample spreading along the frequency range. This global scaling assumes that most energy is contained in the low-frequency range which in turn can improve SNR of the reconstructed image. However, the energy distribution depends mainly on the imaged object (body region) and MR imaging parameters. We hypothesized8 that for similar FOV placements between different subjects, the underlying anatomical structure is also similar. Thus, for analogous imaging parameters the energy distributions exhibit comparable structural shape. This a-priori knowledge can be utilized to provide a local variable-density sampling which improves the sampling efficiency in terms of acquired energy/SNR per sample.
In this work, we improve our previously published purely Cartesian motion imaging sequence9 by a hybrid method which uses a pseudo-spiral trajectory that obeys a local variable-density sampling. Energy distributions for local sampling are estimated from localizer acquisitions of the same subject and up-scaled to the final resolution. Image upscaling is achieved via dictionary learning (DL) or convolutional neural network (CNN) which is trained on a cohort of 37 patients and investigated on 5 volunteers.
Material and Methods
The subsampling mask generation process is depicted in Fig.1. The localizer acquisition at the beginning of the examination is up-scaled to the desired 5D motion imaging resolution. From this up-scaled image, the appropriate FOV can be set and the corresponding power spectrum $$$\mathbf{P}$$$ can be extracted. The normalized spectrum $$$\mathbf{P}_n$$$ adapts locally the eligible distance $$$d(k_y,k_z)$$$ for a 1D Poisson-Disc sampling along a spiral spoke which is gridded to the Cartesian $$$k_y-k_z$$$ subsampling space. In the acquisition for each TR a fully sampled Cartesian readout along $$$k_x$$$ is acquired. One sample after another is acquired in the spoke with distance $$$d(k_y,k_z)$$$ between samples to generate local variable-density. A golden angle increment between consecutive spokes ensures uniform k-space coverage. This hybrid approach allows non-quadratic FOVs. Repeatedly measured low-frequency samples provide respiratory and cardiac self-navigation signals which do not demand any patient interaction, e.g. attachment of belt. These signals can be extracted from the data via principal component analysis3. Retrospective gating and CS reconstruction are implemented into Gadgetron10 to streamline processing.
For image upscaling, decoding $$$\mathbf{D}_L, \mathbf{D}_M$$$ and encoding $$$\mathbf{E}$$$ dictionaries are trained on a database of 37 patients (20 female,60±9y) which were scanned on a 3T PET/MR (Biograph mMR,Siemens) with a localizer $$$\underline{\rho}_L$$$ and motion imaging sequence $$$\underline{\rho}_M$$$1. The model dictionaries $$$\mathbf{D}_L, \mathbf{D}_M$$$ from the patch pairs $$$\mathbf{P}_L, \mathbf{P}_M$$$ are linked over a sparse coding dictionary $$$\mathbf{E}$$$ to a common sparse representation $$$\mathbf{X}$$$
$$\mathbf{P}_M = \mathbf{D}_M \mathbf{E} \mathbf{P}_L = \mathbf{D}_M \mathbf{E} \mathbf{D}_L \mathbf{X}$$
A DL algorithm11 jointly estimates the dictionaries and sparse image. Alternatively, a CNN can be trained for this task. A 3D spoiled GRE sequence (TE=1.23ms,TR=2.6ms,FOV=500x500x360mm,matrixSize=256x256x144,TA=90s) with/without the proposed subsampling is compared against the previous sampling method on 5 volunteers (2 female,30±6y).
Results and Discussion
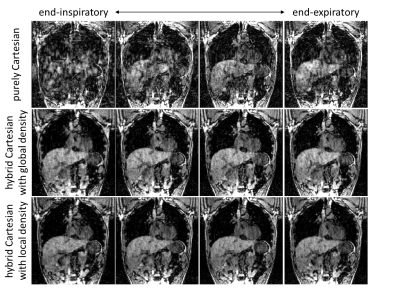
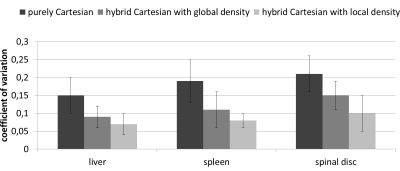
Fig.2 shows a visual comparison of the subsampling masks and reconstructed images of a heavily breathing subject. Reduction of subsampling-related artifacts due to smoother gradient switching can be appreciated as well as in Fig.3 for different breathing states. Fig.4 illustrates the coefficient of variation improvement over all subjects in ROIs of the liver, spleen and spinal disc.Conclusion
Image upscaling provides estimated energy distributions which locally guide the hybrid Cartesian subsampling trajectory. The proposed subsampling improves the overall image quality in terms of SNR by 45% and shows more robustness to subsampling-related artifacts which is beneficial for motion imaging.Acknowledgements
No acknowledgement found.References
[1] T. Küstner, M. Schwartz, P. Martirosian, S. Gatidis, F. Seith, C. Gilliam, T. Blu, H. Fayad, D. Visvikis, F. Schick, B. Yang, H. Schmidt, and N. Schwenzer. MR-based respiratory and cardiac motion correction for PET imaging. Medical Image Analysis, 2017. [2] H. K. Song and L. Dougherty. k-Space weighted image contrast (KWIC) for contrast manipulation in projection reconstruction MRI. Magnetic Resonance in Medicine, 44(6):825–832, 2000. [3] L. Feng, L. Axel, H. Chandarana, K. T. Block, D. K. Sodickson, and R. Otazo. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magnetic Resonance in Medicine, 75(2):775–788, 2016. [4] C. Prieto, S. Uribe, R. Razavi, D. Atkinson, and T. Schaeffter. 3D undersampled goldenradial phase encoding for DCE-MRA using inherently regularized iterative SENSE. Magnetic Resonance in Medicine, 64(2):514–526, 2010. [5] J. Y. Cheng, T. Zhang, N. Ruangwattanapaisarn, M. T. Alley, M. Uecker, J. M. Pauly, M. Lustig, and S. S. Vasanawala. Free-breathing pediatric MRI with nonrigid motion correction and acceleration. Journal of Magnetic Resonance Imaging, 42(2):407–420, 2015. [6] Y. Zhu, Y. Guo, S. G. Lingala, R. M. Lebel, M. Law, and K. S. Nayak. GOCART: GOldenangle CArtesian randomized time-resolved 3D MRI. Magnetic Resonance Imaging, 34(7): 940–950, 2016. [7] F. Han, Z. Zhou, E. Han, Y. Gao, K.-L. Nguyen, J. P. Finn, and P. Hu. Self-gated 4D multiphase, steady-state imaging with contrast enhancement (MUSIC) using rotating cartesian K-space (ROCK): Validation in children with congenital heart disease. Magnetic Resonance in Medicine, 2016. [8] T. Küstner, C. Würslin, S. Gatidis, P. Martirosian, N. Nikolaou, N. Schwenzer, F. Schick, B. Yang, and H. Schmidt. Improving subsampling efficiency for Compressed Sensing MRI. In European Society for Magnetic Resonance in Medicine and Biology (ESMRMB), 2015. [9] T. Küstner, C. Würslin, M. Schwartz, P. Martirosian, S. Gatidis, C. Brendle, F. Seith, F. Schick, N. F. Schwenzer, B. Yang, and H. Schmidt. Self-navigated 4D cartesian imaging of periodic motion in the body trunk using partial k-space compressed sensing. Magnetic Resonance in Medicine, 78(2):632–644, 2017. [10] M. S. Hansen and T. S. Sørensen. Gadgetron: An open source framework for medical image reconstruction. Magnetic Resonance in Medicine, 69(6):1768–1776, 2013. [11] C. Basso, M. Santoro, A. Verri, and S. Villa. PADDLE: Proximal Algorithm for Dual Dictionaries LEarning. In T. Honkela, W. Duch, M. Girolami, and S. Kaski, editors, International Conference on Artificial Neural Networks and Machine Learning (ICANN), pages 379–386, Berlin, Heidelberg, 2011. Springer Berlin Heidelberg. ISBN 978-3-642-21735-7.Figures
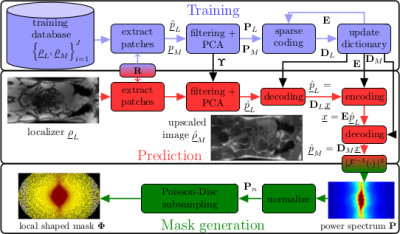
Figure 1: Systematic overview of local shaped mask generation. In a training phase (blue) decoding dictionaries DL, DM and a sparse encoding dictionary E are trained via dictionary learning from image/patch pairs PL, PM consisting of localizer images ρL and motion corrected images ρM. During prediction (red) the upscaled image is estimated from which the power spectrum P is generated. This adapts the subsampling mask generation locally by varying the sampling distance d(ky,kz) along a spiral spoke.