0474

Nonrigid Motion Correction using 3D iNAVs with Generalized Motion Compensated Reconstruction and Autofocusing

Srivathsan Prabu Koundinyan¹, Corey Allan Baron¹, Nicholas Dwork¹, Joseph Yitan Cheng¹, and Dwight George Nishimura¹

¹Electrical Engineering, Stanford University, Stanford, CA, United States

Synopsis

We present a novel framework to combine two well-known methods for motion correction: generalized motion compensated reconstruction (GMCR) and autofocusing. In this hybrid technique, 3D image-based navigators (3D iNAVs) are utilized for motion tracking. The beat-to-beat and voxel-by-voxel motion information within the 3D iNAVs are directly inputted into GMCR to mitigate motion artifacts. To reduce computation time, an autofocusing step is incorporated. The overall correction scheme is evaluated in free-breathing coronary magnetic resonance angiography and renal magnetic resonance angiography exams. In all six in vivo studies, images reconstructed with the proposed strategy outperform those generated with beat-to-beat 3D translational correction.

Introduction

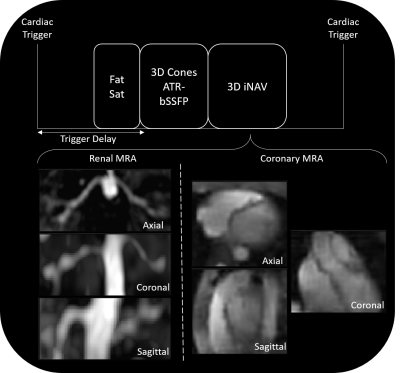
3D image-based navigators (iNAVs) acquired every sequence cycle provide localized motion information of all regions of interest in free-breathing scans¹. In this work, we leverage 3D iNAVs alongside a novel joint generalized motion compensated reconstruction (GMCR) and autofocusing framework to retrospectively mitigate motion artifacts^2,3,4,5. The effectiveness of this nonrigid motion-correction scheme is evaluated in two different free-breathing applications: coronary magnetic resonance angiography (cMRA) and renal magnetic resonance angiography (rMRA)^6,7. Across all six studies, the proposed technique significantly increases vessel sharpness and improves the depiction of renal as well as coronary arteries.

Methods

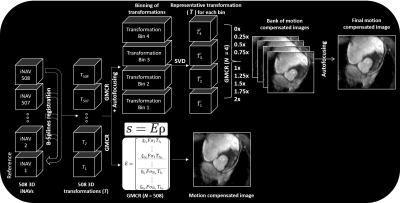
Free breathing cMRA and rMRA scans are performed on a 1.5T GE Signa system using a cardiac-triggered 3D cones sequence. A 3D iNAV of the imaging volume is acquired every heartbeat after collection of the imaging data (Figure 1). The total scan time spans 508 heartbeats. The proposed reconstruction pipeline is comprised of four steps (Figure 2):

(1) The 3D iNAV with the greatest summed similarity, as measured by mutual information, with all other navigators is designated as the reference. Nonrigid alignment of each 3D iNAV to the reference frame is performed using a B-splines registration scheme.

(2) GMCR casts motion correction as the following inverse problem: $$$k = ξFσTρ$$$, where $$$k$$$ is the k-space signal vector, $$$ξ$$$ is the sampling operator, $$$F$$$ is the Fourier transform, $$$σ$$$ is the coil sensitivity, $$$T$$$ is the spatial transformation, and $$$ρ$$$ is the 3D image. When spatial transformations are not available, GMCR provides a motion model predictor. In our case, the 508 beat-to-beat 3D deformation fields from the iNAVs serve as the spatial transformations, and are used to directly solve the inverse problem with LSQR.

(3) In solving the above inverse problem, the computation time scales linearly with the number of distinct spatial transformations in the encoding operator. We reduce the number of spatial transformations by first grouping the deformation fields and corresponding imaging data into four equal-sized bins based on superior-inferior translational motion estimates from the 3D iNAVs. Following this binning, we perform singular value decomposition of the deformation fields within each group, and approximate each cluster of deformation fields as a rank-1 set. With this approach, each deformation field within a group can be represented as a scaled version (with the scale factor determined by the largest singular value and corresponding left singular vector) of the primary right singular vector.

(4) The rank-1 approximation paves the way for invoking an autofocusing algorithm. For each group of deformation fields, the scale factors (normalized to the average scale factor) associated with the primary right singular vector range from 0 to 2 for our datasets. Given this, we reconstruct a bank of nine images using GMCR with scaled versions (scale factors from 0 to 2 in intervals of 0.25) of the primary right singular vector from each of the four groups. From this collection of nine motion-compensated images, a gradient-entropy metric is used to assemble the “best-focused” image on a pixel-by-pixel basis. Note that while nine different reconstructions are now performed to generate the final image with autofocusing, each reconstruction includes only four different transformation operations. Step 2 involves a single reconstruction, but because all 508 beat-to-beat deformation fields are considered, computation time significantly increases.

The proposed nonrigid motion correction technique was evaluated on three free-breathing rMRA scans and three free-breathing cMRA scans. The resulting images were quantitatively and qualitatively compared with those reconstructed with 3D global translational motion correction.

Results

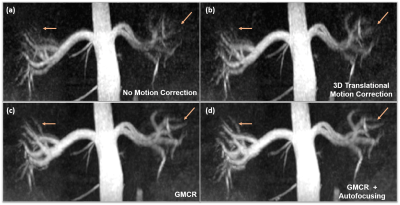
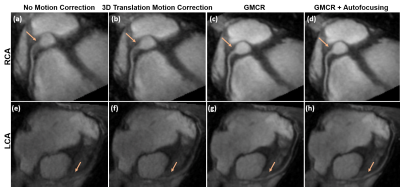
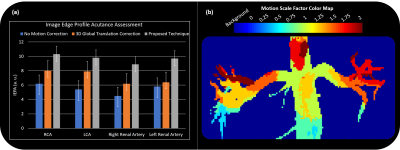
Figure 3 showcases coronal rMRA MIPs from one study using (1) beat-to-beat deformation fields with GMCR and (2) binned deformation fields with GMCR and autofocusing. The result for both schemes is comparable, but, on a GPU, while the former reconstruction took 26.2 hours to complete, the latter completed in 2.7 hours. The reduction in computation time arises from the binning of deformation fields and utilization of autofocusing. Figure 4 highlights the performance of GMCR with autofocusing on a cMRA dataset. Reformatted MIPs show notable improvements in the sharpness of the coronary arteries compared to bulk 3D translational correction. Quantitative vessel sharpness metrics presenting similar trends are shown in Figure 5(a) for all six studies. The autofocusing motion map (Figure 5(b)) demonstrates that scaled versions of the 3D deformation fields contribute to deblurring of different vessels.

Discussion and Conclusion

The proposed technique utilizes the advantages of GMCR and autofocusing to reduce motion blurring of the renal and coronary arteries in free-breathing scans. The incorporation of autofocusing reduces the computation time by a factor of 10, while preserving the result from beat-to-beat motion correction with GMCR alone.

Acknowledgements

We gratefully acknowledge the support of NIH grants R01HL127039, T32HL007846, and T32EB009653. This work was also supported by the Hsi-Fong Ho Stanford Graduate Fellowship, the Ruth L. Kirschstein National Research Award, and the National Science Foundation Graduate Research Fellowship under Grant No. DGE-114747.

References

[1] Addy et al. MRM 74.3 (2015): 614-621.

[2] Batchelor et al. MRM 54.5 (2005): 1273-1280.

[3] Odille et al. MRM 59.6 (2008): 1401-1411.

[4] Odille et al. MRM 60.1 (2008): 146-157.

[5] Cheng et al. MRM 68.6 (2012): 1785-1797.

[6] Luo et al. MRM 77.5 (2017): 1884-1893.

[7] Koundinyan et al. ISMRM Proceedings (2017).

Figures

Figure 1: Timing diagram for free-breathing, non-contrast-enhanced renal MRA and coronary MRA. Following fat saturation, a 3D conical k-space trajectory (28x28x14 cm³ FOV, 1.2 mm isotropic resolution) is utilized to collect imaging data. The acquisition scheme is cardiac triggered, and involves 9137 total interleaved cones acquired in segments of 18 every heartbeat. Immediately after the main data acquisition, a 3D iNAV (28x28x14 cm³ FOV, 4.375 mm isotropic resolution, 176 ms temporal resolution) is collected every heartbeat using 32 cones readouts.

Figure 2: Flowchart of the proposed method. B-splines registration is used to align 3D iNAVs to a reference frame. (Bottom path) The resulting transformations can be directly passed into GMCR for motion compensation. (Top path) Alternatively, for reduced computation time, the transformations can be clustered into four groups. A representative transformation for each group is then computed using SVD. These transformations are scaled by nine factors uniformly ranging from 0 to 2, and inputted into GMCR to form a bank of motion compensated images. The final image is formed by minimizing a gradient entropy metric across this bank.

Figure 3: Coronal renal MRA MIPs from a free-breathing study with (a) no motion correction, (b) 3D translational motion correction, (c) beat-to-beat nonrigid motion correction with GMCR, and (d) autofocusing with GMCR using binned deformation fields for improved computation time. The depiction of the distal left and right renal arteries are similar in (c) and (d), and notably sharper compared to bulk translational correction in (b). Arrows indicate regions of significant improvement.

Figure 4: Reformatted cMRA MIPs from a volunteer study with (a/e) no motion correction, (b/f) 3D translational motion correction, (c/g) GMCR alone, and (d/h) GMCR with autofocusing for the right coronary artery (RCA, top row) and the left coronary artery (LCA, bottom row). The sharpness of both the RCA and LCA undergoes significant improvement upon applying the proposed motion-correction scheme. Arrows highlight improvements in vessel depiction. Although GMCR with autofocusing has a factor of 10 smaller computation time compared to GMCR with beat-to-beat transformations, image quality is similar between the two methods.

Figure 5: (a) Quantitative assessment of vessel sharpness for all six studies using the image edge profile acutance (IEPA) metric demonstrates the superiority of the GMCR and autofocusing framework for motion correction. (b) Color map highlighting which motion scale factors are ultimately used by the joint GMCR and autofocusing algorithm to form the final image for the subject in Figure 3. It is evident that scaled deformation fields contribute to the deblurring of renal vessels. The distal segments of the renal arteries require larger scale factors compared to proximal areas.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

0474