Synopsis

We present a comparison of five different methods that estimate mappings between scanners for diffusion MRI data harmonisation. The methods are evaluated on a dedicated dataset of the same subjects acquired on three distinct scanners with ‘standard’ and ‘state-of-the-art’ protocols, with the latter having higher spatial and angular resolution. Our results show that cross-vendor harmonisation and spatial/angular resolution enhancement of single-shell diffusion data sets can be performed reliably, although some challenges remain. The dataset is available upon request and can serve as a useful testbed for future method development in cross-site/cross-hardware and cross-vendor diffusion MRI harmonisation.

Introduction

MRI data harmonisation is the process of finding a mapping between data sets acquired with different scanners/protocols and making them as comparable as possible. Harmonisation has become a pressing need in the current era of “big data” and multi-center studies, as it can enable the combination of data sets from different MRI scanners^1,2,3. This could dramatically increase the statistical power and sensitivity of clinical studies, with obvious benefits in clinical trials and multi-center research, and enable the transfer of rich information content from state-of-the-art acquisitions to lower quality data⁴, e.g. to enhance resolution.

This work reports a comparison of five different algorithms for diffusion MRI (dMRI) data harmonisation. The algorithms were trained and evaluated on a data set of 14 subjects scanned on three scanners from different vendors and with varying hardware specifications. This study presents details of the dataset which can be used for benchmarking new harmonisation algorithms, and shows the promises and shortcomings of today’s data harmonisation techniques.

Methods

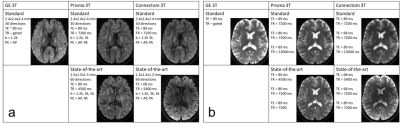
Data: 14 healthy volunteers were scanned on a 3T GE Excite-HDx, 3T Siemens Prisma, and 3T Siemens Connectom scanner. dMRI images were acquired with a ‘standard’ protocol on all three scanners, and a ‘state-of-the-art’ protocol on the latter two (Fig.1a). For the state-of-the-art protocol, we exploited multiband-acquisition and stronger gradients to shorten TE and improve the spatial- and angular resolution per unit time. Additional b=0s/mm² images were acquired with TE and/or TR matching between protocols (Fig.1b), as well as structural MPRAGEs for each scanner. The data is available for researchers upon request.

Tasks: This work focuses on the harmonisation of the lowest b-value shell. The b=0 and 1200s/mm² data from 10 randomly selected subjects were used as training data (all scanners/protocols). The data sets from remaining 4 subjects were used for testing, two tasks were evaluated: 1) scanner-to-scanner harmonisation, predicting the Prisma and Connectom standard data from the GE data; and 2) spatial- and angular resolution enhancement, predicting the Prisma and Connectom state-of-the-art data from the GE data.

Preprocessing: All data were corrected for motion and eddy current-distortions using EDDY⁵, the Prisma and Connectom data were corrected for susceptibility distortions using TOPUP⁶, and the Connectom data corrected for geometric distortions due to gradient nonlinearities⁷. The Prisma and Connectom data were registered to a common space per subject (Prisma standard) using FLIRT⁸, and the GE data using Elastix nonlinear registration thereby correcting for susceptibility distortions^9,10.

Algorithms: Five different harmonisation approaches were tested (Fig.2a), which learnt mappings between spherical harmonic (SH) coefficients or rotationally invariant SH (RISH) features¹¹.

Evaluation: In the four test data sets, diffusion tensor imaging (DTI) and RISH features (FA, MD and R0, R2 respectively) were computed from the predicted data for each test subject and algorithm, and evaluated against the ground truth features derived from the acquired data (Fig.2b). The mean-, mean-normalised-, and mean-squared error were computed globally (in a brain mask excluding cerebellum), regionally (Freesurfer regions¹²) and locally (3x3x3 voxels neighborhood).

Results

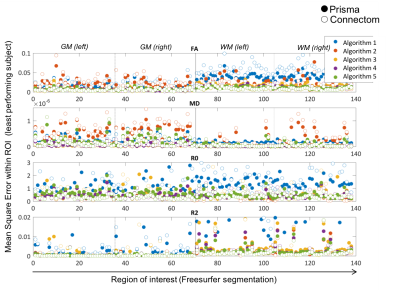
1) Scanner-to-scanner harmonisation: Fig.3 shows the mean-squared error for different Freesurfer regions and different algorithms. Some ROIs have a consistent higher error (e.g. Cingulum), but no systematic trends in the prefrontal cortex were found, where differences in susceptibility correction strategies could affect the result.

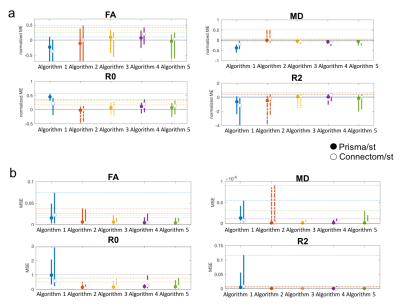
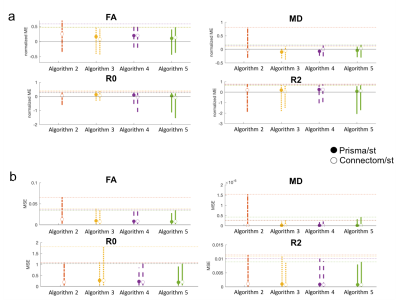
Distributions of the localised errors were computed across all 4 subjects, Fig.4 shows the median and width (95^th percentile) of the a) mean-normalised- and b) mean-squared error. For each metric at least one algorithm has a mean-normalised error below 5%. Algorithms 3 and 5 consistently show the best performance.

2) Spatial- and angular resolution enhancement: Fig.5 shows the median and width of the localised-error distributions. Again both errors vary strongly across metrics. For each metric at least one algorithm has a mean-normalised error lower than 10%, indicating a lower accuracy for this task. The Connectom predictions have overall higher accuracy. Algorithms 4 and 5 consistently show the best performance.

Discussion & Conclusion

We present a comparison of dMRI harmonisation methods that estimate mappings between scanners. The methods rely on deep learning and dictionary learning, are commonly based on SH signal representations, and are capable of harmonising dMRI data to a satisfactory level.

The tested algorithms provide higher accuracy for the scanner-to-scanner harmonisation than for the enhancement task, with the predicted Connectom data having better scores. Considering potential limitations, the lack of reverse phase-encoding acquisitions for susceptibility distortion correction in the GE data may have negatively affected co-registration, and thus reduced algorithm-performance in some ROIs. This could be a general issue for harmonisation of data acquired with different protocols, and is the subject of future work.

Acknowledgements

References

[1] Mirzaalian et al., NeuroImage 135:311-23,2016

[2] Mirzaalian et al., Brain Imaging Behav. doi: 10.1007/s11682-016-9670-y,2017

[3] Fortin et al., NeuroImage 161:149-170,2017;

[4] Alexander et al., NeuroImage 152:283-298,2017

[5] Andersson and Sotiropoulos,NeuroImage 125:1063-1078,2016

[6] Andersson et al.,NeuroImage 20(2):870-888,2003

[7] Glasser et al.,Neuroimage 80:105–124,2013

[8] Jenkinson et al.,NeuroImage 17(2),825-841,2002

[9] Klein et al.,IEEE TMI 29(1),196-205 2010

[10] Irfanoglu et al.,Neuroimage 61(1),275-288,2012

[11] Mirzaalian et al., Med Image Comput Comput Assist Interv. 9349:12-19,2015

[12] Fischl, et al. Neuron 33, 341-355,2002

[13] Shi W et al. arXiv:1609.05158

[14] St-Jean S, et al., Medical Image Analysis 2016; 32: 115-130.

[15] Glasner, D. et al., IEEE ICCV 2009; 349-356.

[16] Golkov V, et al., IEEE Trans Med Imaging 2016; 35(5): 1344-1351.