0467
Robust estimation of diffusion MRI metrics based on slicewise outlier detection (SOLID)1Medical Physics, Radiology, Helsinki University Hospital, Helsinki, Finland, 2Department of Physics, University of Helsinki, Helsinki, Finland, 3Image Sciences Institute, University Medical Center Utrecht, Utrecht, Netherlands, 4Cardiff University Brain Research Imaging Centre, School of Psychology, Cardiff University, Cardiff, United Kingdom
Synopsis
The accurate characterization of diffusion process with MRI is compromised by various artefacts including intensity related errors. If not appropriately accounted for, model estimates can become significantly biased resulting in erroneous metrics. Slicewise intensity errors, in particular, are often handled by excluding the entire image or slice information, or by voxelwise robust estimators that experience difficulties in partial volume regions. In this work, we describe a fast and accurate algorithm to detect slicewise outliers and a framework to incorporate this information as data uncertainty in model estimation algorithms.
Introduction
Slicewise intensity artefacts arising from subject motion or hardware issues can impede the accurate characterization of diffusion with MRI1–4. When not appropriately accounted for, these intensity errors can significantly confound quantitative studies with groups and individuals, and the importance of this problem was once again stressed by recent work5,6. Robust voxelwise estimators are suboptimal to detect slicewise errors, especially when the outlier becomes distributed across multiple slices during the motion correction7–10. Available slicewise detection methods often exclude entire DWIs11 or individual slices5,12–15, which can lead to the unnecessary loss of good data as well as numerical issues16.
We present an automated and fast tool to detect slicewise outliers in multishell dMRI data prior to motion corrections. The framework, coined SOLID (Slicewise OutLIer Detection), naturally incorporates this information as data uncertainty in model estimation. SOLID is based on a straightforward slicewise intensity metric and does not rely on modeling or signal prediction, thereby lifting constraints set on the acquisition protocol by other algorithms5. As the SOLID-informed estimation downweights outliers instead of excluding them, it promotes that the mathematical problem remains well-conditioned and supports the convergence of iterative estimation algorithms17.
SOLID was evaluated using comprehensive diffusion and kurtosis tensor simulations, compared to previously published tools5, and finally validated with dMRI data from 54 newborn subjects in which slicewise outliers were manually labelled.
Methods
Slicewise outlier detection prior to motion correction:
The SOLID framework is visualized in Figure 1. Outlier detection is based on a slicewise intensity metric $$$y_{k,l}$$$ (e.g. variance) calculated from all brain voxels within each slice $$${k}$$$ and DWI $$${l}$$$. Slicewise modified Z-scores18 $$$\zeta_{k,l}$$$ are obtained by computing the median $$$\tilde{y}_{k}$$$ and median absolute deviation $$$\textrm{MAD}_{k}$$$7 (eq.1) across all DWIs (eq.2):
$$\textrm{MAD}_k=1.4826\cdot(|y_{k,l}-\tilde{y}_k|),\tag{1}$$
$$\zeta_{k,l}=\frac{{y_{k,l}-\tilde{y}_k}}{{\textrm{MAD}_k}}.\tag{2}$$
Informed model-estimation after motion correction:
Voxelwise interpolated modified Z-scores are calculated by applying the transformation obtained from motion correction for each DWI $$$\mathbf{T}_{l}(\mathbf{x})$$$ to each corresponding modified Z-score volume $$$\xi_{l}$$$ created from the slicewise modified Z-scores $$$\xi_{k,l}$$$; i.e. $$$\xi_{l}^{'}(\mathbf{x}^{'})=\xi_{l}(\mathbf{T}_{l}(\mathbf{x})))$$$. Subsequently, SOLID weights $$$S_{l}(\mathbf{x}^{'})$$$ between 0 and 1 - representing data uncertainty estimates - are obtained by eq.3:
$$S_{l}(\mathbf{x}^{'})=\left\{\begin{array}{l} 0,\quad if \ \xi_{l}^{'}(\mathbf{x}^{'})>t_{Upper} \\1,\quad if \ \xi_{l}^{'}(\mathbf{x}^{'})<t_{Lower}\\\frac{\xi_{l}^{'}(\mathbf{x}^{'})-t_{Upper}}{t_{Upper}-t_{Lower}},\quad otherwise\end{array}\right. .\tag{3}$$
Modified Z-scores below the lower threshold (suggested $$$t_{Lower}=3.5$$$) are considered normal and have a weight of 1 during model estimation, modified Z-scores above the upper threshold (suggested $$$t_{Upper}=10$$$) are excluded as outliers, and intermediate values get linearly downweighted.
Evaluation:
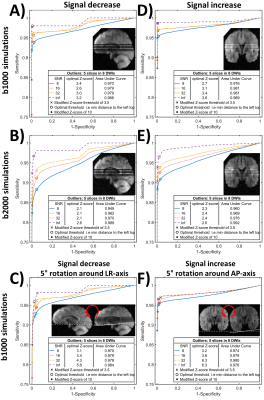
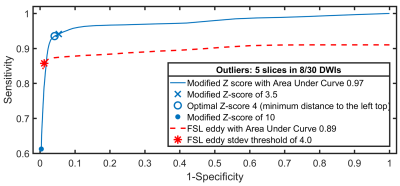
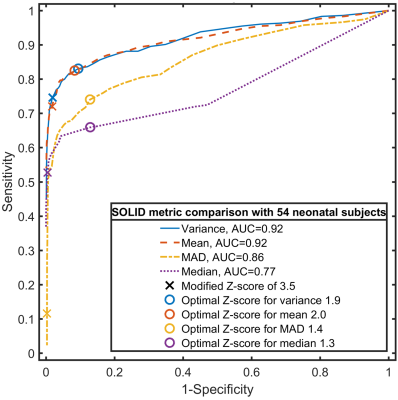
Firstly, outlier detection was evaluated using six sets of 1000 full-brain DWI simulations based on diffusion- and kurtosis tensors obtained from the MASSIVE database18. Each set consisted of 30 DWIs on two shells with b-values 1000s/mm2 and 2000s/mm2, from which eight were replaced with artefactual DWIs having five outlier slices each. Rician noise was introduced with multiple signal-to-noise ratios (SNR). Secondly, SOLID was compared to FSL’s slicewise outlier detection included in EDDY5. Finally, SOLID was validated using manually labeled slicewise outliers from 54 neonatal subjects.
Results & Discussion
Figure 2 shows SOLID receiver-operating-characteristic (ROC) curves for various outlier simulation setups with multiple SNRs. SOLID had a good performance in all simulations as indicated with the lowest recorded area-under-curve (AUC) value of 0.94.
Figure 3 shows a comparison between SOLID and FSL EDDY ROC curves: SOLID overall achieved similar specificity and higher sensitivity compared to EDDY, likely due to the minimum number of voxels per slice required by EDDY.
Figure 4 shows an evaluation of four different slicewise metrics on manually labelled outlier slices in the neonatal dataset, advocating the choice of variance or mean.
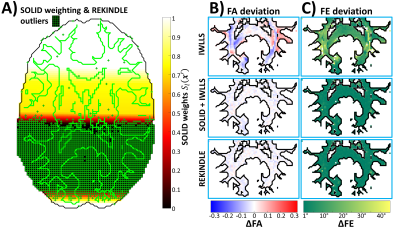
Figure 5 visualizes differences between voxelwise and slicewise outlier detectors in partial-volume-outlier regions, and shows deviations in FA and the first eigenvector (FE) of the diffusion tensor for IWLLS, SOLID-informed IWLLS, and REKINDLE9 estimators. While both robust algorithms did produce similar improvements on the non-robust IWLLS, outliers in partial-volume regions are missed by the voxelwise approach.Conclusion
This study presents SOLID, a fast algorithm to detect and handle slicewise outliers in multi-shell dMRI data. Thorough evaluations with simulations and comparison with an existing tool showed good performance, which was further validated on a ‘gold standard’ dataset with manually labelled outliers from 54 newborn subjects. SOLID could be used in large population studies to quickly highlight the problematic volumes and to avoid biased analyses.Acknowledgements
No acknowledgement found.References
1. Basser, P. J., Mattiello, J. & Lebihan, D. Estimation of the Effective Self-Diffusion Tensor from the NMR Spin Echo. J. Magn. Reson. Ser. B 103, 247–254 (1994).
2 .Stejskal, E. O. & Tanner, J. E. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time‐Dependent Field Gradient. J. Chem. Phys. 42, 288–292 (1965).
3. Jones, D. K. & Cercignani, M. Twenty-five pitfalls in the analysis of diffusion MRI data. NMR Biomed. 23, 803–820 (2010).
4. Le Bihan, D., Poupon, C., Amadon, A. & Lethimonnier, F. Artifacts and pitfalls in diffusion MRI. J. Magn. Reson. Imaging 24, 478–488 (2006).
5. Andersson, J. L. R., Graham, M. S., Zsoldos, E. & Sotiropoulos, S. N. Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. Neuroimage 141, 556–572 (2016).
6. Andersson, J. L. R. & Sotiropoulos, S. N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078 (2016).
7. Mangin, J. F., Poupon1, C., Clark, C., Le Bihan, D. & Bloch, I. Eddy-current distortion correction and Robust tensor estimation for MR diffusion imaging. Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics) 2208, 186–194 (2001).
8. Pannek, K., Raffelt, D., Bell, C., Mathias, J. L. & Rose, S. E. HOMOR: Higher Order Model Outlier Rejection for high b-value MR diffusion data. Neuroimage 63, 835–842 (2012).
9. Tax, C. M. W., Otte, W. M., Viergever, M. A., Dijkhuizen, R. M. & Leemans, A. REKINDLE: Robust Extraction of Kurtosis INDices with Linear Estimation. Magn. Reson. Med. 73, 794–808 (2015).
10. Chang, L. C., Walker, L. & Pierpaoli, C. Informed RESTORE: A method for robust estimation of diffusion tensor from low redundancy datasets in the presence of physiological noise artifacts. Magn. Reson. Med. 68, 1654–1663 (2012).
11. Oguz, I. et al. DTIPrep: quality control of diffusion-weighted images. Front. Neuroinform. 8, 4 (2014).
12. Zhou, Z. et al. Automated artifact detection and removal for improved tensor estimation in motion-corrupted DTI data sets using the combination of local binary patterns and 2D partial least squares. Magn. Reson. Imaging 29, 230–242 (2011).
13. Liu, Z. et al. Quality control of diffusion weighted images. in Proceedings of SPIE--the International Society for Optical Engineering 7628, 76280J (NIH Public Access, 2010).
14. Li, Y. et al. Image Corruption Detection in Diffusion Tensor Imaging for Post-Processing and Real-Time Monitoring. PLoS One 8, e49764 (2013).
15. Pannek, K. et al. Automatic Detection of Volumes Affected by Subvolume Movement. Proc. 25th Sci. Meet. Int. Soc. Magn. Reson. Med. (2017).
16. Sairanen, V., Kuusela, L., Sipilä, O., Savolainen, S. & Vanhatalo, S. A novel measure of reliability in Diffusion Tensor Imaging after data rejections due to subject motion. Neuroimage 147, 57–65 (2017).
17. Batchelor, P. G., Atkinson, D., Hill, D. L. G., Calamante, F. & Connelly, A. Anisotropic noise propagation in diffusion tensor MRI sampling schemes. Magn. Reson. Med. 49, 1143–1151 (2003).
18. Froeling, M., Tax, C. M. W., Vos, S. B., Luijten, P. R. & Leemans, A. MASSIVE brain dataset: Multiple acquisitions for standardization of structural imaging validation and evaluation. Magn. Reson. Med. 77, 1797–1809 (2017).
Figures
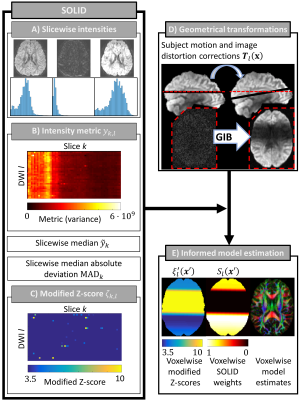
Outlier
detection and the SOLID-informed estimation framework. A) Measured intensities
for voxels $$$\mathbf{x}$$$ are used to calculate slice $$${k}$$$ and DWI $$${l}$$$ specific B) metric $$$y_{k,l}$$$, median $$$\tilde{y}_{k}$$$, and median absolute deviation $$$\textrm{MAD}_{k}$$$ to evaluate the modified Z-score (C). D) Image
registration is used to correct the geometrical misalignments and results gradual
intensity bands (GIB) due to the slicewise outliers. The
transformation matrices $$$\mathbf{T}_{l}(\mathbf{x})$$$ are
applied to the modified Z-scores. E) Voxelwise modified Z-scores $$$\xi_{l}^{'}(\mathbf{x}^{'})$$$ in the corrected image space are mapped to a
value between 0 (outlier) and 1 (normal data) forming SOLID weights $$$S_{l}(\mathbf{x}^{'})$$$
i.e. data uncertainties.