0464
Multi-shell SHARD reconstruction from scattered slice diffusion MRI data in the neonatal brain1Centre for the Developing Brain, School of Imaging Sciences and Biomedical Engineering, King's College London, London, United Kingdom
Synopsis
Diffusion MRI (dMRI) offers a unique probe into neural connectivity in the developing brain. However, analysis of neonatal brain imaging data is complicated by inevitable subject motion. Here, we develop a method for reconstructing multi-shell HARDI data from scattered slices, jointly estimating an uncorrupted data representation and per-excitation (slice or multiband package) motion parameters. The reconstruction relies on orthogonal decomposition of multi-shell dMRI data using a bespoke spherical harmonics and radial decomposition (SHARD), together with outlier rejection, distortion, and slice profile correction. We evaluate the method on publicly-released datasets for 40 neonatal subjects from the developing Human Connectome Project.
Introduction
Accounting for unavoidable subject motion is a crucial requirement in neonatal diffusion MRI (dMRI). Assuming that motion is frozen within the short readout time of each EPI shot, the natural data unit is the slice or multiband excitation. Motion correction then requires co-registering the resulting set of scattered slices in an anatomical reference frame1-8, while simultaneously accounting for diffusion-weighted contrast variation and gradient reorientation9. Moreover, individual slices within any given volume may be differently affected by motion-induced rotation, introducing scatter in the effective diffusion gradient direction. Addressing this requires a joint image-space and q-space data representation that can be evaluated for any gradient orientation and b-value.
We therefore propose a data-driven orthonormal linear representation of the signal, termed spherical harmonic and radial decomposition (SHARD), and adopt an inverse problem perspective, in which the underlying SHARD representation of the dMRI signal and slice motion parameters are jointly optimized to best explain the acquired data.
Method
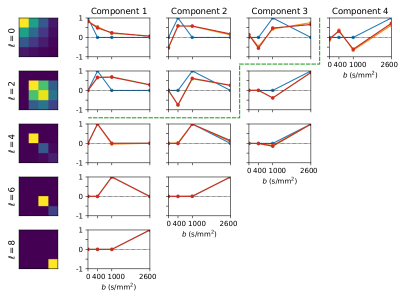
SHARD basis: This is constructed using singular value decomposition of the SH coefficients per harmonic band across shells (see Figure 1), thus learning the covariance between shells from the data. SHARD offers both high-fidelity data representation, and optimal low-rank data approximation helpful during registration (see below).
Forward model: The uncorrupted data is represented in a 4-D image $$$\vec{x}$$$ of SHARD reconstruction coefficients. The dMRI contrast in all reoriented gradient directions is calculated with the linear operator $$$Q_{\vec{\mu}}\,\vec{x}$$$. The operator $$$M_{\vec{\mu}}$$$ then projects the resulting images to scanner space using cubic spline interpolation, based on the rigid head motion parameters $$$\vec{\mu}$$$. Finally, the signal in every slice is predicted by convolution with a Gaussian slice sensitivity profile via the operator $$$B$$$.
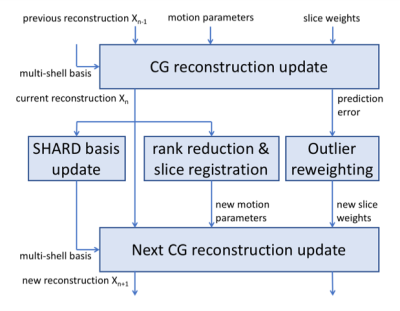
We then seek the optimal $$$\vec{x}^\ast$$$ and rigid motion parameters $$$\vec{\mu}^\ast$$$ that maximize similarity between $$$\vec{y}$$$ and its prediction: $$\vec{x}^\ast, \vec{\mu}^\ast = \arg\min_{\vec{x}, \vec{\mu}} \| \vec{y} - B M_{\vec{\mu}} Q_{\vec{\mu}} \vec{x} \|^2 + \lambda \|L \vec{x} \|^2$$ where the second term is a Laplacian regularizer, added to stabilise the super-resolved reconstruction in the slice direction. The optimization process alternatingly optimizes reconstruction parameters $$$\vec{x}$$$ and motion parameters $$$\vec{\mu}$$$, as outlined in the flowchart in Figure 2. Individual steps are detailed below.
Reconstruction: Given a current motion estimate, the reconstruction step calculates the maximum likelihood estimate of the uncorrupted signal $$$\vec{x}$$$ in a sparse least-squares problem (approximate dimensions 184M x 55M for these data), using a conjugate gradient solver. A B0-fieldmap (static w.r.t. the moving subject) is also incorporated to correct susceptibility-induced distortion.
Registration: Motion parameters are updated using rigid image registration. A 3-D template is generated for every target slice, as a rank-reduced signal prediction based on the slice’s diffusion gradient encoding and current motion estimate. Motion parameters are subsequently median-filtered in temporal order to minimise outliers during registration.
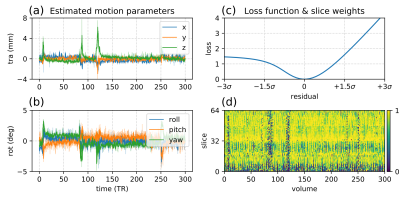
Outlier reweighting: Outlier slices manifest primarily as signal dropouts, and to lesser extent as altered image intensity due to spin history. We thus reweight slices based on an asymmetric loss function of the mean residual error per slice within a brain mask (see Figure 3c).
Experiments
Data: Brain dMRI from 40 neonates scanned at term age for the developing Human Connectome Project: 3T Philips Achieva; TE/TR=90/3800ms; MB=4; SENSE=1.2; resolution 1.5x1.5x3mm with 1.5mm slice overlap. Diffusion gradient encoding with b=0s/mm2 (20), b=400s/mm2 (64), b=1000s/mm2 (88), b=2600s/mm2 (128) with interleaved phase encoding10.
Setup: Data was preprocessed with image denoising11 and Gibbs-ringing removal12. A field map was estimated from b=0 images with FSL Topup13. Reconstruction was run for 3 iterations (the first one constrained to volume-level motion) with regularization $$$\lambda = 0.02$$$. The reconstruction uses a SHARD decomposition of rank = 89 (allowing for SH order $$$\ell_{max}$$$ = 0, 4, 6 and 8 for respective shells); registration operates at reduced rank = 15. Computation time amounts to 2h per subject on an 8-core i7 processor.
Results and Discussion
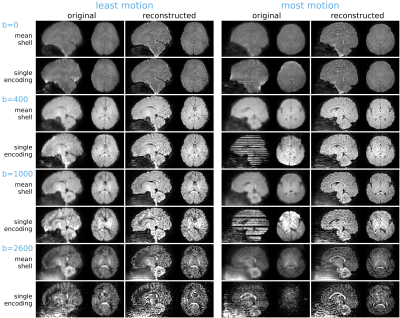
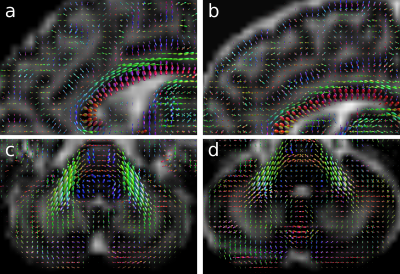
Motion estimates and outlier slice weights are shown in Figure 3 for a representative subject. The head position is stable for extended periods of time, with sudden bursts of motion in between, corresponding also with increased rate of outlier detection. Reconstructions of the subjects with least and most motion are visually compared in Figure 4, showing successful correction of even highly corrupted data. Note that the approach inherently ensures consistent alignment across shells without the need for explicit post-hoc registration. Figure 5 shows fibre orientation distributions in these reconstructed data using a 2-tissue factorization14.Conclusion
We developed a method for multi-shell slice-to-volume reconstruction in dMRI using a bespoke q-space basis with desirable rank-reduction properties, and demonstrated successful results in a neonatal brain imaging cohort.Acknowledgements
This work was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z), MRC strategic grant MR/K006355/1 and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.
This work received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/20072013)/ERC grant agreement no. 319456 (dHCP project), and was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z), MRC strategic grant MR/K006355/1 and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.
References
- Jiang S, Xue H, Counsell S. Diffusion tensor imaging (DTI) of the brain in moving subjects: application to in-utero fetal and ex-utero studies. MRM 2009; 62(3):645-55.
- Gholipour A, Estroff JA, Warfield SK. Robust super-resolution volume reconstruction from slice acquisitions: Application to fetal brain MRI. IEEE TMI 2010; 29(10):1739-1758.
- Kuklisova-Murgasova M, Quaghebeur G, Rutherford M, et al. Reconstruction of fetal brain MRI with intensity matching and complete outlier removal. MedIA 2012; 16(8):1550-1564.
- Oubel E, Koob M, Studholme C, et al. Reconstruction of scattered data in fetal diffusion MRI. MedIA 2012; 16(1):28-37.
- Scherrer B, Gholipour A, Warfield S. Super-resolution reconstruction to increase the spatial resolution of diffusion weighted images from orthogonal anisotropic acquisitions. MedIA 2012; 16(7): 1465-1476.
- Fogtmann M, Seshamani S, Kroenke C, et al. A unified approach to diffusion direction sensitive slice registration and 3-D DTI reconstruction from moving fetal brain anatomy. IEEE TMI 2014; 33(2):272-289.
- Kuklisova-Murgasova M, Daducci A, Lockwood-Estrin G, et al. Reconstruction of fetal diffusion MRI using a spherical harmonic model. ISMRM 2017; 25:1747.
- Andersson JLR, Graham MS, Drobnjak I, et al. Towards a comprehensive framework for movement and distortion correction of diffusion MR images: Within volume movement. NeuroImage 2017; 152:450-466.
- Leemans A, Jones DK. The B-matrix must be rotated when correcting for subject motion in DTI data. MRM 2009; 61(6):1336-49.
- Hutter J, Tournier J-D, Price AN, Cordero-Grande L, et al. Time-efficient and flexible design of optimized multi-shell HARDI diffusion. MRM 2017; in press.
- Veraart J, Novikov DS, Christiaens D, et al. Denoising of diffusion MRI using random matrix theory. NeuroImage 2016;142:394-406.
- Kellner E, Dhital B, Kiselev V, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. MRM 2016;76(5):1574-1581.
- Andersson JLR, Skare S, and Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 2003; 20(2):870-888.
- Christiaens D, Sunaert S, Suetens P, Maes F. Convexity-constrained and nonnegativity-constrained spherical factorization in diffusion-weighted imaging. NeuroImage 146:507-517.
Figures