0463

Diffusion Acceleration with Gaussian process Estimated Reconstruction (DAGER)
Wenchuan Wu1, Peter J Koopmans2, Jesper Andersson1, and Karla L Miller1

1Wellcome Centre for Integrative Neuroimaging, FMRIB, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom, 2Erwin L. Hahn Institute for Magnetic Resonance Imaging, Essen, Germany

Synopsis

Diffusion acceleration is a challenging task, particularly when using simultaneous multi-slice (SMS) imaging with in-plane acceleration. In this work, we develop a method termed DAGER: Diffusion Acceleration with Gaussian process Estimated Reconstruction, to improve SMS with in-plane acceleration, achieving a total acceleration factor of 12 (MB=4, R=3). In addition, DAGER reconstruction doesn't cause major degradation of angular resolution, indicating the Gaussian process model used in DAGER can accurately estimating the degree of local smoothness in q-space.

Introduction

As neuroscience studies aim for higher spatial and angular resolution, image acceleration is an increasingly important part of the diffusion MRI (dMRI) toolkit. As acceleration factors increase, the reconstruction problem becomes ill-conditioned, particularly when using both in-plane acceleration1-2 and simultaneous multi-slice (SMS) imaging3-4. Rather than reconstructing each volume independently, we propose to constrain reconstruction by incorporating information from the angular (q) domain. One property that is exploited in dMRI analysis is smoothness of the signal in q-space. Gaussian processes (GPs) have utilized this property to remove eddy currents and replace outlier images5-6. Building on these approaches, we have developed DAGER: Diffusion Acceleration with Gaussian process Estimated Reconstruction. A preliminary account demonstrated DAGER for high in-plane acceleration7 (Fig.1). We now use DAGER to improve SMS with in-plane acceleration (SMS-DAGER), achieving a total acceleration factor 12. We further present a Bayesian framework that incorporates estimation of GP hyper-parameters, with no need for manual tuning.

Theory and Methods

A linear dMRI signal model can be expressed as d=Au+n with d and u denoting the k-space data and unknown images for all diffusion volumes. A is the system matrix combining sensitivity encoding, Fourier encoding and k-space sampling operations. n is the measurement noise. With a GP prior on the dMRI signal5, the maximal a posteriori estimation of the image can be derived based on a Bayesian formulation:$$ \mathbf{u} = \underset{\mathbf{u}} {\text{argmin}}\left( \frac{1}{2{\sigma_n}\!^2} \parallel{\mathbf{A} {\mathbf{u}}-\mathbf{d}}\parallel^2_2 + \frac{1}{2}(\mathbf{P}^{\text{H}}\mathbf{u} - \boldsymbol{\mu})^\mathrm{H} (\mathbf{\Sigma}\otimes \mathbf{I}_{N_i})^{-1}(\mathbf{P}^{\text{H}}\mathbf{u} - \boldsymbol{\mu})\right) \;\;\;\;\;\;[1]$$

where the first term is the data fidelity (log-likelihood) and the second term describes the GP prior. Elements of the covariance matrix $$$\mathbf{\Sigma}$$$ capture the local smoothness in q-space with a spherical function specified by three hyper-parameters5. $$$\mathbf{P}$$$ is the motion-induced phase errors, which can be measured using a navigator or estimated from the image data8. $$$\mathbf{I}$$$ is an identity matrix; $$$N_i$$$ is the number of voxels; $$$\boldsymbol{\mu}$$$ is the prior mean. $$$\otimes$$$ is the Kronecker product; $$$\sigma_n$$$ is the noise variance. The hyper-parameters are determined by the data, and ideally should be determined before solving Eq.[1]. Here, we iterate between hyper-parameter estimation and image reconstruction.

SMS data were acquired from four subjects at 7T. Scan parameters: total acceleration 12 (MB=4, R=3), SSH-EPI readout with blipped-CAIPI, 84 slices, 1.5mm3 isotropic resolution, 32ch coil, 156×156 matrix, TR/TE=3500ms/71ms, b=1000s/mm2, 192 diffusion directions, total acquisition time ~11mins. A locally incoherent k-q sampling scheme was used9. In addition, single-band (SB) comparison data were acquired that were matched to the above protocol with the following exceptions. In one subject, three repetitions using the same sequence parameters but only 21 slices to match TR. For other subjects, the same number of slices, requiring TR=12000ms and only 50 directions to match acquisition time. DAGER and SENSE reconstructions were analysed with tensor fitting, multi-fibre estimation and probabilistic fibre tractography10-12.

Results

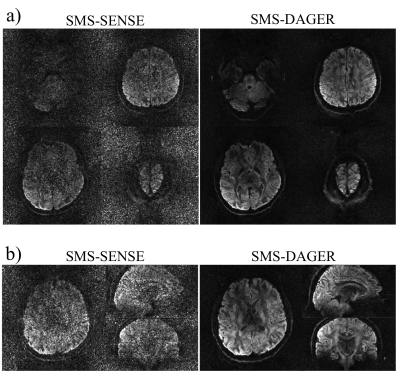
Fig.2 shows the reconstruction of in-vivo SMS data. Conventional SENSE has amplified noise due to the high acceleration both through-plane and in-plane. The DAGER reconstruction produces high-quality images with effectively suppressed noise and aliasing artefacts.

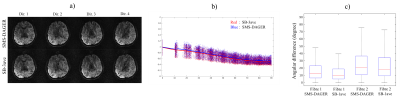
One potential concern with DAGER is whether the GP model might reduce effective angular resolution. This was investigated using the high-SNR reference dataset in one subject. Fig.3a qualitatively demonstrates consistency between SMS-DAGER results and the SB reference. Fig.3b quantifies whole-brain covariance of the in-vivo dMRI signal as a function of the distance between two directions. Angular blurring would increase covariance in DAGER, but SMS-DAGER results yield a very similar covariance to SB-3ave. Fig.3c compares fibre orientations between SMS-DAGER and the SB reference estimated using BEDPOSTX and the mean fibre orientations. The angular differences for SMS-DAGER images are comparable to the conventional single-band data with slightly higher angular differences (<4° measured by the median).

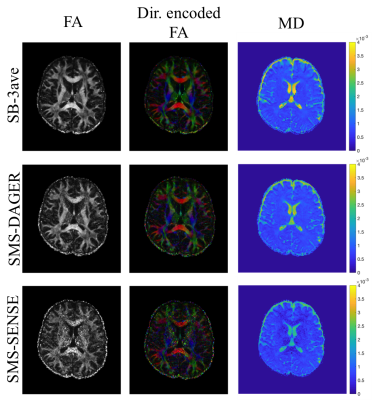
Fig.4 compares tensor fits, where metrics derived from SMS-DAGER reconstructions are of similar quality as the high-SNR SB-3ave reference, while conventional SENSE results are visibly noisier.

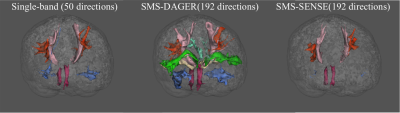
Fig.5 shows 14 major white matter tracts generated using a standardized tractography protocol, AutoPtx12. The SENSE reconstruction fails to capture many fibre tracts. The DAGER reconstruction enables delineation of an abundance of tracts, including several passing through crossing-fibre regions, which can hardly be found from the SB reference or SMS-SENSE reconstruction.

Discussion and Conclusion

DAGER is a novel k-q method for reconstructing accelerated dMRI data that utilizes correlations between q-space samples to improve k-space reconstruction. In-vivo results show superior performance of DAGER compared with conventional parallel imaging methods at high acceleration factors. Further, DAGER achieves this without major degradation of angular resolution, suggesting that GP hyper-parameters are accurately estimating the degree of local smoothness in q-space.

Acknowledgements

Funding for this work was provided by the Marie Curie Initial Training Network program (FP7-PEOPLE-2012-ITN-316716, WW) and Wellcome Trust fellowships (091509/Z/10/Z, KM).

References

  1. Pruessmann, K.P., Weiger, M., Scheidegger, M.B. and Boesiger, P., 1999. SENSE: sensitivity encoding for fast MRI. Magnetic resonance in medicine, 42(5), pp.952-962.
  2. Griswold, M.A., Jakob, P.M., Heidemann, R.M., Nittka, M., Jellus, V., Wang, J., Kiefer, B. and Haase, A., 2002. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic resonance in medicine, 47(6), pp.1202-1210.
  3. Setsompop, K., Gagoski, B.A., Polimeni, J.R., Witzel, T., Wedeen, V.J. and Wald, L.L., 2012. Blipped‐controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g‐factor penalty. Magnetic Resonance in Medicine, 67(5), pp.1210-1224.
  4. Setsompop, K., Cohen-Adad, J., Gagoski, B.A., Raij, T., Yendiki, A., Keil, B., Wedeen, V.J. and Wald, L.L., 2012. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage, 63(1), pp.569-580.
  5. Andersson, J.L. and Sotiropoulos, S.N., 2015. Non-parametric representation and prediction of single-and multi-shell diffusion-weighted MRI data using Gaussian processes. Neuroimage, 122, pp.166-176.
  6. Andersson, J.L. and Sotiropoulos, S.N., 2016. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage, 125, pp.1063-1078.
  7. Wu W, Koopmans PJ, Andersson JR, Miller KL. Accelerated k-q diffusion MRI reconstruction using Gaussian processes. ISMRM 25th Annual Meeting & Exhibition, Honolulu, USA, 2017.
  8. Chen, N.K., Guidon, A., Chang, H.C. and Song, A.W., 2013. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage, 72, pp.41-47.
  9. Wu W, Koopmans PJ, Miller KL. Design of a locally incoherent sampling scheme for improved joint k-q reconstruction of diffusion MRI. ISMRM 25th Annual Meeting & Exhibition, Honolulu, USA, 2017.
  10. T.E.J. Behrens, M.W. Woolrich, M. Jenkinson, H. Johansen-Berg, R.G. Nunes, S. Clare, P.M. Matthews, J.M. Brady, and S.M. Smith. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med, 50(5):1077-1088, 2003.
  11. T.E.J. Behrens, H. Johansen-Berg, S. Jbabdi, M.F.S. Rushworth, and M.W. Woolrich. Probabilistic diffusion tractography with multiple fibre orientations. What can we gain? NeuroImage, 23:144-155, 2007.
  12. De Groot, M., Vernooij, M.W., Klein, S., Ikram, M.A., Vos, F.M., Smith, S.M., Niessen, W.J., Andersson, J.L.R., 2013. Improving alignment in Tract-based spatial statistics: Evaluation and optimization of image registration. NeuroImage, 76, 400-411.

Figures

Fig.1. Illustration of DAGER reconstruction for in-plane acceleration. Local smoothness in q-space is used as a constraint to improve the reconstruction of k-space data. Incoherent k-space sampling is used in each q-space neighbourhood to improve the reconstruction performance.

Fig.2. Reconstruction of in-vivo SMS data. On the top shows SMS-SENSE reconstruction and SMS-DAGER reconstruction of four simultaneously acquired slices. On the bottom shows three orthogonal planes of the reconstructed images using the two methods.

Fig.3. a) Example images for SMS-DAGER (top, 11mins, 84 slices) and the high-SNR reference SB-3ave (bottom, average of three SB datasets, 33 mins, 21 slices). b). Signal covariance of the reconstructed dMRI images as a function of the angular difference between two directions. The mean covariance is plotted as solid line and is fairly similar for the two datasets. c) Evaluation of the difference in fibre orientations between the SB-2ave reference (averaging two repetitions) and the fibre orientation estimated from SMS-DAGER or SB-1ave data. There is slightly better agreement between the reference and SB-1ave.

Fig.4. Comparison of tensor fitting results.

Fig.5. White matter fibre tracts generated using AutoPtx. 14 fibre tracts are shown here, including uncinate fasciculus (blue), superior thalamic radiation (pink), cingulate gyrus part of cingulum (cyan), superior longitudinal fasciculus (red), acoustic radiation (green), posterior thalamic radiation (ivory), and medial lemniscus (ruby). SMS data reconstructed with DAGER support the delineation of an abundance of tracts, whereas the single-band data (less directions to match the scan time) and the SMS data reconstructed with SENSE fail to capture many tracts.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0463