Synopsis

In this work, we propose a novel joint manifold learning and sparsity aware framework for highly accelerated cardiac cine imaging. The proposed method efficiently captures the intrinsic low dimensional nonlinear manifold geometry and inherent periodicity of cardiac data, and outperforms the current state-of-the-art accelerated MRI methods.

Introduction

Current techniques for accelerated dMRI from reduced k-space data are posed as a constrained inverse problem using global data a-priors such as low rank^[1-3] and sparsity^[4-6], built around the input linear space. Such techniques completely neglect local data geometry and complex nonlinear characteristics of dMRI^[7-9]. In this work, we will present a joint nonlinear manifold learning and sparsity-aware framework for dMRI. The proposed framework essentially captures the underlying nonlinear data geometry and integrates the well known sparse prior for highly accelerated cardiac MRI.

Methods

Let the dynamic image series be represented by a $$$N\times N_{\text{fr}}$$$ Casorati matrix $$$\mathbf{X}=[\mathbf{x}_{1},\mathbf{x}_{2},\ldots\mathbf{x}_{N_{\text{fr}}}]$$$, where $$$N=N_{\text{p}}\times N_{\text{f}}$$$ (Number of phase encoding lines$$$\times$$$ Number of frequency encoding lines) where each column $$$\mathbf{x}_{i}$$$ is the $$$i^{th}$$$ image. Given a highly under-sampled $$$M\times N_{\text{fr}},M<<N$$$ k-space data $$$\mathbf{Y}$$$, such that $$$\mathbf{Y} = \mathbf{\phi}(\mathbf{X})+\mathbf{V},$$$ where $$$\mathbf{\phi}$$$ is a measurement operator that incorporates Fourier under-sampling along each column of $$$\mathbf{X}$$$ and $$$\mathbf{V}$$$ stands for noise, our goal is to reconstruct unknown dynamic image series $$$\mathbf{X}$$$. To solve such an ill-posed problem, we pose it as the following joint manifold learning and sparsity aware optimization problem:

$$\arg\min\nolimits_{\;\mathbf{X}}\left\|\mathbf{Y}-\mathbf{\phi}(\mathbf{X})\right\|_{\text{F}}^2+\alpha \left\|\cal{E}(\mathbf{X})\right\|_{\text{p}}+\lambda\left\|{\cal{S}}(\mathbf{X})\right\|_1,^{(1)}$$

where $$${\cal{S}}(\cdot)$$$ is a sparsifying transform and $$$\cal{E}$$$ embeds high dimensional ($$$N$$$) dMR images into low dimensional ($$$d$$$) smooth manifold $$$\cal{M}$$$ and preserves some geometric property $$$\cal{G}$$$ in norm-$$$\text{p}$$$ sense. To solve (1), our framework integrates several modules:

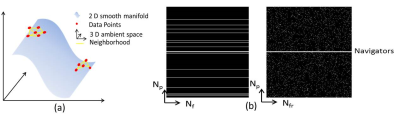
1.Manifold learning and low dimensional embedding: Signals in high dimensional input space including dMR images often lie on or close to a smooth low dimensional manifold^[9-11] (Fig.1(a)). Similarly as in other manifold learning task our first objective is to learn the manifold geometry $$$\cal(G)$$$ that describes dMRI manifold. To learn such manifold geometry we postulate that, each image $$${\mathbf{x}}_i,i=1,2,\ldots{\mathbf{N}}_{\text{fr}}$$$ can be represented as an affine combination of other images in dMRI^[9,11] series such that:

$$\boldsymbol{\omega}_{i}\in \underset{\boldsymbol{\omega}_{i}^{H}\mathbf{1}_{N_{\text{fr}}}=1,\, \omega_{i}^{i}=0}{\operatorname{argmin}}\left\|\mathbf{x}_{i}-\sum\nolimits_{n=1}^{N_{\text{fr}}} \omega_{i}^{n}\mathbf{x}_n\right\|^{2}+\beta\left\|\boldsymbol{\omega}^{i}\right\|_{1},^{(2)}$$

where $$$\mathbf{1}_{N_{\text{fr}}}$$$ is the all-one vector. The constraint $$$\boldsymbol{\omega}_{i}^{H} \mathbf{1}_{N_{\text{fr}}}=1$$$, where $$$(\cdot)^{{H}}$$$ denotes Hermitian transposition, ensures affine neighboring relations, $$$\omega_{i}^{i}=0$$$ excludes $$$\mathbf{x}_i$$$ from being a neighbor of itself, and $$$\beta\geq 0$$$ enforces sparsity. Because training images are not available in our problem, capitalizing linearity of Fourier transform, we use few navigator signals (low frequency harmonics) from the k space of each image (Fig.1(b)) to learn such affine geometry, hence the so-called self-learned approach. Let $$$\mathbf{W}$$$ be a $$$N_{\text{fr}}\times N_{\text{fr}}$$$ weight matrix that describes the manifold geometry $$$\cal{G}$$$. Then $$$d<<N$$$ basis that preserves the geometry $$$\cal{G}$$$ is given by the $$$d$$$ Eigen vectors $$${\boldsymbol{\Psi}}^{H}=[\boldsymbol{\psi}_{1},\boldsymbol{\psi}_{2},\ldots \boldsymbol{\psi}_{d} ]$$$ of an $$$N_{\text{fr}}\times N_{\text{fr}}$$$ matrix $$$\boldsymbol{\mathcal{K}}:=(\mathbf{I}-\mathbf{W})(\mathbf{I}-\mathbf{W})^{{H}}, \mathbf{I}$$$ being an Identity matrix. Hence, for $$$\text{p}=2$$$, the second term in (1) can be replaced by expressing image series as: $$$\mathbf{X}=\mathbf{U}\boldsymbol{\Psi}$$$ to get:

$$\arg\min\nolimits_{\;\mathbf{U}}\left\|\mathbf{Y}-\mathbf{\phi}(\mathbf{U}\boldsymbol{\Psi})\right\|_{\text{F}}^2+\lambda\left\|{\cal{S}}(\mathbf{U}\boldsymbol{\Psi})\right\|_1.^{(3)}$$

2.Sparsity enforcement: Several sparse transformation $$$\cal{S}(\cdot)$$$ can be used in our framework. For cardiac cine imaging we use well-known Fourier transformation such that (3) takes the form:

$$\arg\min\nolimits_{\;\mathbf{U}}\left\|\mathbf{Y}- \mathbf{\phi}\left({\mathbf{U}}\boldsymbol{\Psi}\right)\right\|_{\text{F}}^2+\lambda \left\|{\mathbf{U}}\boldsymbol{\Psi}_{f}\right\|_{1},^{(4)}$$

where $$$\boldsymbol{\Psi}_{f}=\boldsymbol{\Psi}\mathbf{F}$$$ with $$$\mathbf{F}$$$ being a Fourier matrix.

3.Image reconstruction: To solve (4), we use half quadratic minimization strategy^[12]. We introduce an auxiliary variable $$$\mathbf{Z}={\mathbf{U}}\boldsymbol{\Psi}_{f}$$$ such that (4) takes the form of,

$$\arg\min \nolimits_{\;\mathbf{U},\mathbf{Z}}\left\|\mathbf{Y}-\mathbf{\phi}\left({\mathbf{U}}\boldsymbol{\Psi}\right)\right\|_{\text{F}}^2+\frac{\lambda}{2\delta} \left\|\mathbf{U}\boldsymbol{\Psi}_{f}-\mathbf{Z}\right\|_{\text{F}}^2+\lambda\left\|\rho\left( \mathbf{Z}\right)\right\|_{1},^{(5)}$$

where $$$\rho(\cdot)$$$ is a vectorizing operator, $$$\delta$$$ is a threshold.^[12] The problem in (5) can be solved iteratively alternating over $$$\mathbf{U}$$$ and $$$\mathbf{Z}$$$. At $$$(t)^{th}$$$ iteration,

$$\mathbf{Z}^{(t)}=\arg\min\nolimits_{\;\mathbf{Z}}\;\frac{1}{2\delta}\left\|\mathbf{U}^{(t-1)}\boldsymbol{\Psi}_{f}-\mathbf{Z}\right\|_{\text{F}}^2+\left\|\rho\left(\mathbf{Z}\right)\right\|_{1},^{(6)}$$

$$\mathbf{U}^{(t)}=\arg\min\nolimits_{\;\mathbf{U}}\left\|\mathbf{Y}-\mathbf{U}\boldsymbol{\Psi}\right\|_{\text{F}}^2+\frac{\lambda}{2\delta}\left\|\mathbf{U}\boldsymbol{\Psi}_{f}-\mathbf{Z}^{t}\right\|_{\text{F}}^{2}.^{(7)}$$

Problem (6) can be solved using soft thresholding^[12] and (7) can be solved using conjugate gradient method. Finally, the desired dynamic magnetic image series can be computed using $$$\mathbf{X}=\mathbf{U}\boldsymbol{\Psi}$$$.

Results

The proposed method is verified by extensive testing on several cardiac data.

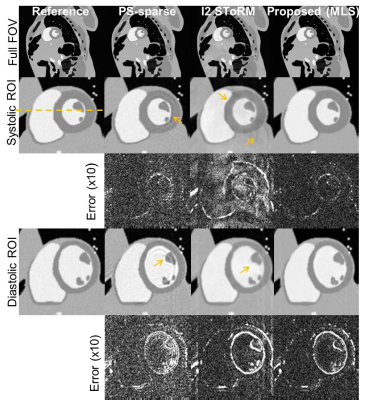
Cardiac cine phantom: An MRXCAT^[13] phantom was used to generate breath-held cardiac cine data of matrix size $$$(N_{\text{p}}\times N_{\text{f}}\times N_{\text{fr}})\;408\times 408\times 360.$$$ Retrospective undersampling was performed using 14 phase encoding lines per frame out of which 4 were navigators, and a net reduction factor of 32.

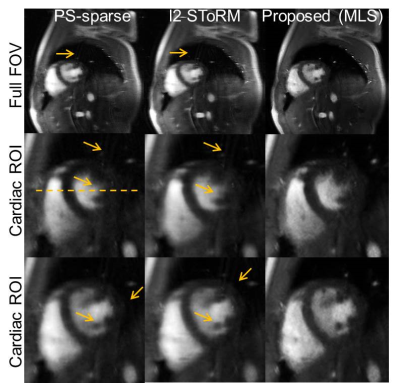
Real-time free-breathing cardiac cine: Short-axis two chamber view, prospectively undersampled cardiac cine acquisition was acquired using FLASH sequence. The acquisition parameters used were $$$TR/TE = 5.8/4~ms$$$, $$$FOV=284\times 350~mm$$$, spatial resolution $$$=1.8~mm$$$. The data matrix was of size $$$156\times 192\times 310$$$ each in 12 channels. 14 phase encoding lines per frame were acquired, out of which 4 were navigators, resulting in a reduction factor of about 11.

Form Figs 2-5, it can be seen that the proposed method outperforms both PS-sparse^[5] and SToRM^[7]. We have seen that PS-sparse suffers from ripple like and low-resolution artifacts, while SToRM gives cleaner images but suffers from blocky artifacts.

Conclusion

Acknowledgements

The authors would like to thank Institute for Biomedical Engineering, ETH Zurich for making the phantom data available online. Also, thanks to Drs. Z-P.Liang and A. Christodoulou for helping on acquiring real-time cardiac cine data. This work is supported in part by the National Science Foundation (NSF) CCF-1514403, NSF1514056 and the National Institute of Health R21EB020861.

References

1. Z.-P. Liang, “Spatiotemporal imaging with partially separable functions,”in Biomedical Imaging (ISBI), IEEE International Symposium on, April 2007, pp. 988–991.
2. S. Lingala, Y. Hu, E. Dibella, and M. Jacob, “Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR,” Medical Imaging,IEEE Transactions on, vol. 30, pp. 1042–1054, 2011.
3. H. Jung, J. C. Ye, and E. Y. Kim, “Improved k-t BLAST and k-t SENSE using FOCUSS,” Physics in medicine and biology, vol. 52, no. 11, p.3201, 2007.
4. M. Lustig, D. Donoho, and J. M. Pauly, “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magnetic Resonance in Medicine, vol. 58, no. 6, pp. 1182–1195, 2007.
5. B. Zhao, J. P. Haldar, A. G. Christodoulou, and Z.-P. Liang, “Image reconstruction from highly undersampled (k,t)-space data with joint partial separability and sparsity constraints,” Medical Imaging, IEEE Transactions on, vol. 31, pp. 1809–1820, 2012.
6. D. Liang, E. V. DiBella, R.-R. Chen, and L. Ying, “k-t ISD: Dynamic cardiac MR imaging using compressed sensing with iterative support detection,” Magnetic Resonance in Medicine, vol. 68, no. 1, pp. 41–53, 2012.
7. S. Poddar and M. Jacob, “Dynamic MRI using smoothness regularization on manifolds (SToRM),” Medical Imaging, IEEE Transactions on,vol. 35, no. 4, pp. 1106–1115, April 2016.
8. U. Nakarmi, Y. Wang, J. Lyu, D. Liang, and L. Ying, “A kernel-based low-rank KLR model for low-dimensional manifold recovery in highly accelerated dynamic MRI,” Medical Imaging, IEEE Transactions on,no. 99, 2017.
9. U. Nakarmi, K. Slavakis, J. Lyu, and L. Ying, “M-MRI: A manifold based framework to highly accelerated dynamic magnetic resonance imaging,” in Biomedical Imaging (ISBI), IEEE International Symposium on, April 2017, pp. 19–22.
10. S. T. Roweis and L. K. Saul, “Nonlinear dimensionality reduction by locally linear embedding,” Science, vol. 290, no. 5500, pp. 2323–2326,2000.
11. K. Slavakis, G. B. Giannakis, and G. Leus, “Robust sparse embedding and reconstruction via dictionary learning,” in Information Sciences and Systems (CISS), 47th Annual Conference on, March 2013, pp. 1–6.
12. D. Geman and C. Yang, “Nonlinear image recovery with half quadraticregularization,” Image Processing, IEEE Transactions on, vol. 4, no. 7,pp. 932–946, July 1995.
13. L. Wissmann, S. Claudio, S. William P, and K. Sebastian, “MRXCAT:Realistic numerical phantoms for cardiovascular magnetic resonance,”Journal of Cardiovascular Magnetic Resonance, vol. 16, no. 1, 2014.