0435

Direct and Fast Learning of Fiber Orientation Distribution Function for Tractography
Ting Gong1, Hongjian He1, Zhichao Lin2, Zhiwei Li2, Qiqi Tong1, Yi Sun3, Feng Yu2, and Jianhui Zhong1,4

1Center for Brain Imaging Science and Technology, Key Laboratory for Biomedical Engineering of Ministry of Education, College of Biomedical Engineering and Instrumental Science, Zhejiang University, Hangzhou, China, 2Department of Instrument Science & Technology, Zhejiang University, Hangzhou, China, 3MR Collaboration NE Asia, Siemens Healthcare, Shanghai, China, 4Department of Imaging Sciences, University of Rochester, Rochester, NY, United States

Synopsis

Multi-shell, multi-tissue, constrained spherical deconvolution is an appealing method for the reconstruction of fiber orientation distribution function (fODF), which is of great importance for solving complex fiber configurations to achieve reliable tractography. However, many diffusion measurements and multiple reconstruction steps are required. In this study, the deep neural network were employed to form a multi-output regression problem for establishing a fast and direct estimation of fODF. The proposed method offers a new streamlined reconstruction procedure which exhibits great potential for accelerating the reconstruction of fODF with whole-brain coverage, with satisfactory accuracy in two minutes.

Introduction

Fiber Orientation Distribution Function (fODF) is a probability distribution on a sphere that is critical for resolving multiple fiber orientations in tractography. 1 More precise fODF estimates could be achieved by multi-shell, multi-tissue, constrained spherical deconvolution (MSMT-CSD), 2 but they requires a long acquisition time with multiple reconstruction steps. Inspired by the method of inferring quantitative diffusion measures directly from down-sampled DWIs, 3 here we propose a fast and direct reconstruction method of more sophisticated fODFs by appling the deep neural network (DNN).

Method

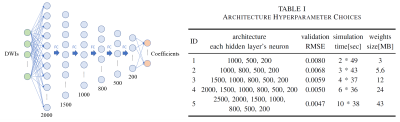
We use the DNN to form a multi-output regression problem, with a spherical harmonics (SH)-based representation of fODFs as the target output, which lowers the requirement for network structure and provides a smooth representation of the data distributed on a sphere, compared to amplitude-represented fODFs. In our DNN method, down-sampled DWIs are used as input and SH coefficients as the output, directly avoiding any intermediate steps. Several options of depth and width were tested for the DNN architecture, and the 2000-1500-1000-800-500-200 setting was chosen for a balance between performance and cost of time and memory, as shown in Figure 1 and Table I.

The ethics committee of the local institute approved this human study. The DWI data were collected from three healthy subjects on a MAGNETOM Prisma 3T MR scanner (Siemens Healthcare, Erlangen, Germany) equipped with a 64-channel head-neck coil using a single-shot EPI sequence: TR/TE= 7000/67 ms, FOV= 210×210 mm2, number of slices= 50, and resolution= 2.5×2.5×2.5 mm3. Diffusion weightings of b = 1000, 2000, and 3000 s/mm2 were applied in 23, 45, and 68 directions 4 with 14 b = 0 images equally entered, resulting in a total of 150 DWIs. In addition, b = 0 images with an opposite phase-encoding direction were also acquired.

After DWI preprocessing for motion and distortion correction, 5 MSMT-CSD reconstruction was performed in MRtrix (http://www.mrtrix.org/) using an unsupervised method.6 fODF was represented by the SH series of the order lmax, amounting to (lmax +1)(lmax +2)/2 SH coefficients. Based on the highest recommended order of 8, 7 the training labels were set as the 45 fODF SH coefficients reconstructed from all 150 DWIs. One subject’s data were reserved for testing whereas 90% of the other two subjects’ data were used for training, and 10% constituted a validation set. Keras 8 was used for training and testing with Tensorflow running backend. 9 All the codes were run on a platform with an NVIDIA GTX-1080 graphics card and CUDA Deep Neural Network library10 installed.

Results

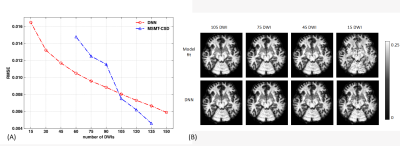
When decreasing the DWIs, the overall root-mean-squared errors of the DNN on whole brain white matter rose gently and were lower than the MSMT-CSD reconstruction after its sharp jump from 105 to 90 DWIs, as shown in Figure 2. The first SH coefficient showed that detailed structures are still maintained for the DNN method at 15 DWIs, whereas it is mostly lost for model reconstruction, indicating its unreliable fODF estimates.

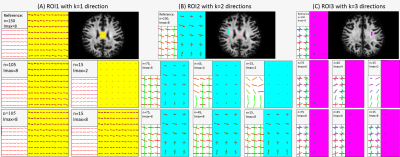
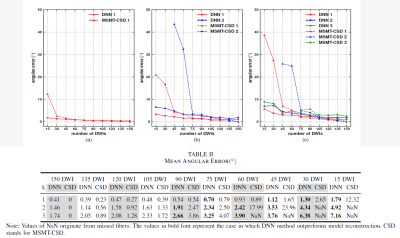
The fODFs of three typical ROIs corresponding to k=1, 2, and 3 fiber directions are depicted in Figure 3, and its statistics of angular errors are shown in Figure 4. The reducing DWIs cause a decreasing lmax in the model reconstruction results, leading to less discriminating fODF lobes and a failure of recovery of less obvious directions when the DWIs are fewer than 45 in two fiber regions and 75 in three fiber regions. In the DNN method, the morphology of fODFs remains intact, even when the DWIs decrease to 15. The steady trend of solid curves in Figure 4 suggests that the DNN method preserves the information contained in the original data very well. The smaller angular errors suggest that the DNN outperforms the model reconstruction when the DWIs are fewer than 105.

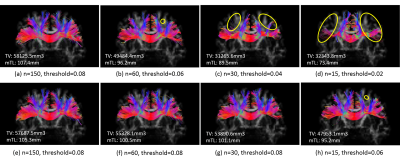
Finally, fiber tractography using extracted peaks from fODFs was conducted to validate the effectiveness of the learned fODFs. The model-reconstructed results miss several large branches of fibers, causing severe track volume loss and track length truncation when n is less than 60.

Discussion

In contrast to a previous work that determined fiber directions by first inferring the number of directions before downgrading to a classification problem in predefined directions, 11 our DNN method is end-to-end. Full representation of fODF is recovered and can be sampled in arbitrary directions, thus retaining more information, including the uncertainty around each of the estimated orientations and their respective volume fractions.

Conclusion

This DNN-based, fast fODF reconstruction method provides a new approach to resolve complex fiber configurations, making whole-brain multi-fiber tractography feasible in two minutes, which is beneficial in clinical practice.

Acknowledgements

This work was supported by the National Key R&D Program of China (2017YFC0909200), National Natural Science Foundation of China (81401473, 91632109) and the Fundamental Research Funds for the Central Universities (2017QNA5016).

References

1. Jeurissen B, Leemans A, Jones D K, et al. Probabilistic fiber tracking using the residual bootstrap with constrained spherical deconvolution. Human Brain Mapping, 2011, 32(3): 461-479.

2. Jeurissen B, Tournier J, Dhollander T, et al. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage, 2014: 411-426.

3. Golkov V, Dosovitskiy A, Sperl J I, et al. q-Space Deep Learning: Twelve-Fold Shorter and Model-Free Diffusion MRI Scans. IEEE Transactions on Medical Imaging, 2016, 35(5): 1344-1351.

4. Caruyer E, Lenglet C, Sapiro G, et al. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magnetic Resonance in Medicine, 2013, 69(6): 1534-1540.

5. Andersson J L, Sotiropoulos S N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage, 2016: 1063-1078.

6. Dhollander T, Raffelt D, Connelly A. Unsupervised 3-tissue response function estimation from single-shell or multi-shell diffusion MR data without a co-registered T1 image. Proc. ISMRM Workshop on Breaking the Barriers of Diffusion MRI, vol. 5, 2016.

7. Tournier J, Calamante F, Connelly A, et al. Determination of the appropriate b value and number of gradient directions for high‐angular‐resolution diffusion‐weighted imaging[J]. NMR in Biomedicine, 2013, 26(12): 1775-1786.

8. Chollet F et al., “Keras,” https://github.com/fchollet/keras, 2015.

9. Abadi M, Barham P, Chen J, et al. TensorFlow: a system for large-scale machine learning. operating systems design and implementation, 2016: 265-283.

10. Chetlur S, Woolley C, Vandermersch P, et al. cuDNN: Efficient Primitives for Deep Learning. arXiv: Neural and Evolutionary Computing, 2014.

11. Koppers S, Merhof D. “Direct estimation of fiber orientations using deep learning in diffusion imaging.” in Proc. MLMI. Springer, 2016, pp. 53–60.

Figures

Figure 1. Network architecture used in this work. The network depth and width are determined by conducting an error rate test on an independent validation set, as shown in Table I. When decreasing the number of DWIs, the maximum order of SH also decreases for the model reconstruction method, causing a loss of angular resolution. However, for the DNN based method, a maximum order of 8 can always be achieved with 45 output SH coefficients.

Figure 2. (A) The overall root-mean-squared error of all 45 coefficients of the DNN method (red) and model reconstruction method (blue) in brain white matter, estimated from different numbers of DWIs. The reference standard is a model reconstruction result using 150 DWIs. Model reconstruction could not generate responses of lmax 8 when the DWIs were fewer than 60. (B) The first SH coefficient, which is the only interpretable coefficient, represents the contrast of total apparent fiber density per voxel, thus conveying structural information. The blurred structure from model fitting with 15 DWIs indicates its unreliable fODF estimates.

Figure 3. fODFs and extracted peak directions of three typical ROIs of (A) single, (B) two, and (C) three fiber regions (k=1, 2, 3), where n is the number of DWIs and lmax is the SH order. (Top) Reference results from the model reconstruction with all the DWIs, (middle) model-reconstructed results for reduced n and lmax, and (bottom) the DNN results for reduced n and lmax of 8. The reduced DWIs cause decreased order in the model reconstruction method, whereas a highest recommended order of 8 can always be achieved for the DNN.

Figure 4. The angular error (◦) for the three ROIs containing a (a) single fiber, (b) two fibers, and (c) three fibers. The solid line represents the DNN, and the dashed line represents the model reconstruction. The DNN exhibits a steady performance in these conditions, particularly when the number of DWIs is limited. In such a case, the model reconstruction method cannot infer the correct number of fibers and the angular error is unacceptable. The mean angular errors obtained by taking the mean of the whole k directions are listed in Table II.

Figure 5. Fiber tractography comparison. A whole brain seeding deterministic tractography [46] was conducted with 1000 tracks extracted for each case using the same ROI on the body of the corpus callosum. (a-d) Results from 150, 60, 30, and 15 DWIs with model reconstruction; (e-f) results from 150, 60, 30, and 15 DWIs with the DNN. The track volume (TV) and mean track length (mTL) are listed for each case. The yellow circles mark the missing branches.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0435