0382

Faster T2 Shuffling with Wave-encoding
Siddharth Srinivasan Iyer1,2, Berkin Bilgic1, and Kawin Setsompop1

1Athinoula A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 2Department of Electrical Enginerring and Computer Science, Massachussets Institute of Technology, Cambridge, MA, United States

Synopsis

T2-shuffling is a recently proposed approach that can reconstruct multiple, sharp T2-weighted images from a single fast spin-echo (FSE) scan. Wave-CAIPI is a parallel imaging technique that uses additional sinusoidal gradients to spread aliasing in the readout direction, to take full advantage of coil-sensitivity information in highly accelerated rectilinear acquisitions. In this work, we augment T2-shuffling with wave-encoding and examine the ability of this combined approach in accelerating FSE acquisition that can achieve multiple T2-weighted images reconstruction. We demonstrate the efficacy of our technique through a 2D simulation, where wave-encoding was shown to provide good reconstruction at 2-3x higher accelerations.

Introduction

T2-shuffling1 is a recently introduced novel acquisition/reconstruction method for volumetric, fast spin-echo (FSE) imaging that can reconstruct multiple sharp T2-weighted images from a single scan. It leverages random under-sampling in the phase-encode directions and spatiotemporal low-rank priors to achieve high rates of acceleration, allowing for scan times of around 6–7 minutes. Wave-CAIPI2 is a parallel-imaging technique that utilizes additional sinusoidal gradients during the readout to spread aliasing in the readout direction. This was shown to improve the acceleration capabilities of parallel-imaging as it enables full use of 3D coil-sensitivity information, resulting in a better posed inverse problem. In this work, we examine the incorporation of wave-encoding into T2-shuffling to provide higher rates of acceleration.

Forward Model

The T2-shuffling forward model can be described as:

$$y=MFE\Phi\alpha$$

where $$$y$$$ is the acquired data, $$$M$$$ is the sampling mask, $$$F$$$ is the Fourier Transform, $$$E$$$ is the ESPIRiT3 coil-sensitivity operator, $$$\Phi$$$ is the T2-temporal basis and $$$\alpha$$$ are the temporal coefficients.

The augmented T2-shuffling with wave-encoding can be described as:

$$y=MF_yWF_xE\Phi\alpha$$

where $$$W$$$ is the wave’s point spread function (PSF) in $$$(k_x, y)$$$ space.

Methods

Simulations were performed to compare standard T2-shuffling to the augmented T2-shuffling with wave-encoding.

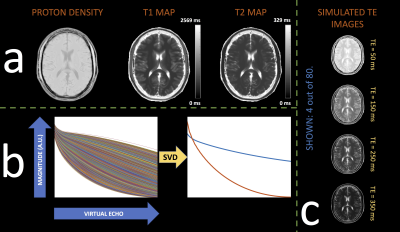
Signal model: Realistic T1, T2 and proton density maps (at resolution=1x1mm and FOV=256x256mm) were obtained from the Brainweb database4 (courtesy of Dr. Bo Zhao). This was used to generate a time-series of T2-weighted images of a FSE acquisition, along with a corresponding T2-shuffling temporal basis, where an echo-spacing of 5ms was used for the simulation. The variable flip angle train (of 83 length) and FSE-simulation code used were obtained from the T2-shuffling support code repository5. Figure 1 illustrates the parameter maps, the T2-basis and the time series of images. From the T2-basis simulation, it was determined that two temporal coefficients were sufficient to capture approximately 98% of the data, and therefore will be used in all shuffling reconstruction.

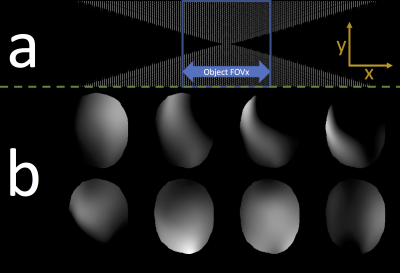
Coil sensitivity and Wave-encoding: To model multi-channel data, BART6 was used first to generate an 8-channel Shepp-Logan phantom and then to calibrate ESPIRiT coil maps from the phantom’s k-space data. For Wave-encoding, the wave PSF was generated assuming the application of a 6 cycle Gy sine-wave during the kx readout of duration 3ms, using max gradient amplitude of 40mT/m and slew of 180T/m/s. The resulting ESPIRiT maps and wave PSF (i.e. voxel spreading along x) are depicted in Figure 2.

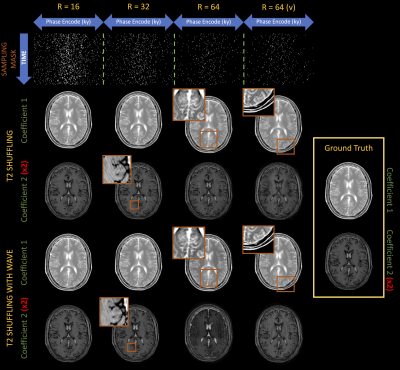
Under-sampling experiments: 2D imaging simulations were performed, where at each time point (or T2-weighted TE image), the phase encode direction (ky) was under-sampled. Four different variable-density random sampling masks were generated using VISTA7’s code repository8: at 16-fold acceleration, 32-fold acceleration and with two at 64-fold acceleration. The 16-fold, 32-fold and the first 64-fold sampling masks have identical sampling density distributions over time, and the second 64-fold acceleration mask has a sampling density that varies from less to more uniform over time. These are illustrated at the top of Figure 3.

Reconstruction was done iteratively with a locally-low rank (llr) soft-threshold applied to the coefficient images each iteration. Identical llr thresholds and maximum number of iterations were used for both T2 shuffling and T2-shuffling with wave-encoding.

Results

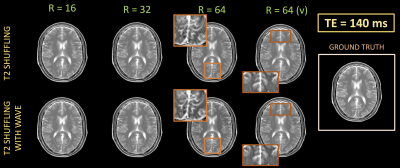
Figure 3 shows T2-coefficients for both standard T2-shuffling and T2-shuffling with wave-encoding at various accelerations, where wave-reconstructed coefficients have less streaking artifacts in all cases. It should be noted that first coefficient is significantly more dominant than the second. In the R=32 case, wave-encoding mitigates the large cross-thatching artifacts in the second coefficient map of standard T2-shuffling, to achieve good reconstruction. In the two R=64 cases, the wave case also has much less artifacts, with the second coefficient performance improving by using the sampling mask whose sampling uniformity varies over time (i.e. 64(v)). In Figure 4, we see the resulting virtual T2-weighted images at TE of 140ms. The R=16 and R=32 cases look similar for both reconstructions, but in the two R=64 cases, significantly better performance was achieved through wave-encoding, where the cross-thatching artifacts are nicely mitigated.

Discussion

Wave-augmented T2-shuffling improves image quality at higher accelerations compared to standard T2-shuffling. This should allow for a 2-3x increase in achievable acceleration. The use of a sampling mask that shifts from a more non-uniform to a more uniform sampling distribution was motivated intuitively by observing that the later T2 images had sharper edges due to the slower T2 of CSF in the brain, and this was demonstrated in simulation to improve reconstruction at high accelerations. Further investigation into sampling mask optimization will be performed in conjunction of 3D FSE simulation and in vivo experiments that are underway.

Acknowledgements

This work was supported in part by NIH research grants: R01EB020613, R01EB019437, R24MH106096, P41EB015896, and the shared instrumentation grants: S10RR023401, S10RR019307, S10RR019254, S10RR023043.

References

  1. Tamir J, Uecker M, Chen W, Lai P, Alley M, Vasanawala S, Lustig M. T2-Shuffling: Fast, multi-contrast volumetric fast spin echo imaging. Magn. Reson. Med. 2016; doi: 10.1002/mrm.26102
  2. Bilgic B, Gagoski B, Cauley S, Fan A, Polimeni J, Grant P, Walk L, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magn. Reson. Med. 2014; doi:10.1002/mrm.25347
  3. Uecker M, Lai P, Murphy J, Virtue P, Elad M, Pauly J, Vasanawala, S, Lustig M. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014; doi: 10.1002/mrm.24751
  4. Collins D, Zijdenbos A, Kollokian V, Sled J, Kabani N, Holmes C, Evans A. Design and construction of a realistic digital brain phantom. IEEE Trans. Med. Imaging, vol. 17, pp. 463–468. 1998.
  5. Located at https://github.com/jtamir/t2shuffling-support (from the commit dated at September 29, 2016).
  6. Tamir J, Ong F, Cheng J, Uecker M, Lustig M. Generalized Magnetic Resonance Image Reconstruction using The Berkeley Advanced Reconstruction Toolbox. ISMRM Workshop on Data Sampling and Image Reconstruction, Sedona. 2016. 1.
  7. Ahmad R, Xue H, Giri S, Ding Y, Craft J, Simonetti O. Variable density incoherent spatiotemporal acquisition (VISTA) for highly accelerated cardiac MRI. Magn. Reson. Med. 2014; 10.1002/mrm.25507
  8. Located at https://github.com/osu-cmr/vista (from the commit dated at June 29, 2015)

Figures

Figure 1: (a) The brain parameter maps used to simulate the FSE images. (b) Ensemble of FSE signals that are used to obtain the T2 shuffling temporal basis via the singular value decomposition (SVD). (c) Subset of the time-series of images to exemplify the multiple contrast images over time.

Figure 2: (a) Wave PSF in (x, y) space, demonstrating the voxel spreading effect along x that varies linearly with y (b) ESPIRiT coil maps used in the parallel-imaging forward model. BART was used to generate an 8-channel Shepp-Logan phantom and to calibrate the ESPIRiT maps from the phantom’s k-space data.

Figure 3: The reconstructed temporal coefficients from accelerated data at various accelerations (Ry), denoted at top of figure. The (v) denotes the case where sampling mask has a more non-uniform sampling density at the start of the echo train and a more uniform sampling density towards the end. For R=16 case, we see similar performance in both methods. For R=32 case, we see similar first coefficient performance with wave reconstructing a better second coefficient image. In the two R=64 cases, the wave reconstruction has significantly fewer artifacts, with the second coefficient performance improving by using the (v) sampling mask.

Figure 4: The resulting T2 weighted image at the effective TE of 140ms. In the R=64 cases, we see significant reduction in cross-thatching artifacts when Wave-encoding is used.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0382