0378
Chirp-Encoded 3D GRE and MPRAGE sequences1Monash Biomedical Imaging, Monash University, Melbourne, Australia, 2School of Psychological Sciences, Monash University, Melbourne, Australia, 3Department of Electrical and Computer System Engineering, Monash University, Melbourne, Australia, 4School of Software and Electrical Engineering, Swinburne University of Technology, Melbourne, Australia, 5Institute of Medicine, Research Centre Juelich, Juelich, Germany
Synopsis
Non-Fourier encoding such as random, noiselets and chirp encoding have demonstrated image quality improvement in accelerated compressive sensing (CS) MRI applications. However, implementation of the non-Fourier encoding schemes in 2D spin echo sequence limits its use in practice, due to the fact that spin echo is inherently a slow sequence. In this work, we present a novel implementation of chirp encoding in fast 3D gradient echo (GRE) and MPRAGE sequences. The chirp encoding scheme is compared with conventional Fourier encoding for compressive sensing and susceptibility weighted imaging applications. The evaluation demonstrates that chirp encoding is able to preserve spatial resolution better than the Fourier encoding.
Introduction
Non-Fourier encoding schemes such as random,1 chirp 2, toeplitz 3 and noiselets 4 have shown performance improvement in compressive sensing and parallel imaging. Despite the advantages provided by non-Fourier encoding, there are certain practical limitations with the non-Fourier encoding. One of the limitations is the implementation in an inherently slow spin echo sequence. Further, non-Fourier encoding schemes are not compatible with the turbo spin echo sequence that limits its use for practical purposes, as the turbo spin echo sequence is normally used in the clinical setting. An alternative is to implement non-Fourier encoding in GRE sequences, although slice selection is one of the problems with the 2D GRE sequences. Therefore, in this work we present an implementation of chirp encoding for the fast 3D GRE sequence where slice selection can be achieved by oversampling in readout direction. A 3D chirp-encoded pulse sequence is designed using real time spatially selective RF pulses, and the application of chirp encoding in compressive sensing (CS) and susceptibility weighted imaging (SWI) is evaluated.Methods
Pulse sequence design
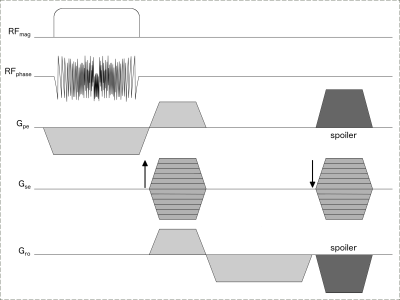
A 3D GRE pulse sequence is designed as shown in Fig.1, that encodes the primary phase encoding (PE) direction with the chirp and other two directions with Fourier. For N PE, a total of N different spatially selective RF excitation pulses is required to acquire the chirp-encoded k-space data. Due to the hardware constraint on the scanner, which limits the number of different RF pulses to 128, the RF pulses are prepared in real time for each PE. The gradient required during the excitation RF pulse is given by:
$$G_y= \frac{1}{\gamma \hspace{3pt} FOV_{pe} \hspace{3pt} \Delta t_{p} }$$
where γ is gyromagnetic ratio, FOVpe is field of view in PE direction, Δtp is dwell time of RF pulse.
CS Simulation
Simulations were performed on a phantom image to determine the effect of chirp encoding in CS reconstruction. The k-space of a phantom image was under-sampled by a factor of 4 and 6, and the reconstructed images using multichannel compressive sensing (MCS)4 was evaluated. To simulate chirp-encoded data, the PE direction was encoded with chirp basis and readout was encoded with Fourier basis. The chirp basis is constructed by modulating each row of the Fourier basis with a modulation function defined as:
$$C(n) = e^{j (\Delta c \hspace{1 pt} n^2 + \Delta c)}$$
where n is phase encode number and Δc is chirp encoding factor.
Multichannel compressive sensing reconstruction
The acquired data were under-sampled using complete random under-sampling for chirp and variable density under-sampling for Fourier. The images were reconstructed with MCS4 reconstruction by solving the following optimization:
$$Min_{\widehat{x}} \hspace{3mm} \lambda_1\|\Psi \widehat{x}\|_{l_1} + \lambda_2\| TV \widehat{x}\|_{l_1} + \|Y-E \widehat{x}\|_{l_2}^2$$
where, ψ is the wavelet transform operator, TV is the total variation operator and λ1, λ2 are the regularization parameters.
Imaging Parameters
Two sequences, 3D GRE and MPRAGE were evaluated for chirp and Fourier encoding. The imaging parameters for flow compensated GRE were: TE/TR = 20/30 ms, flip angle = 100, FOV = 256x256x192 mm3 and resolution 1 mm isotropic. For the MPRAGE sequence the TE/TR = 5/2000 ms, and the other parameters were same as GRE. The data were acquired in a 3T MAGNETOM Skyra, Siemens Healthineers, Erlangen, Germany.
Results
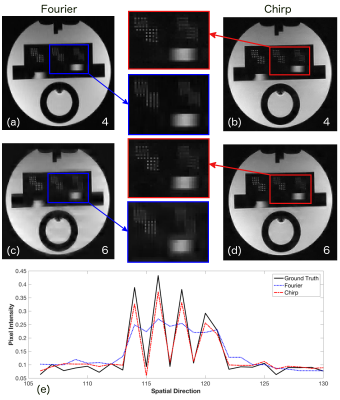
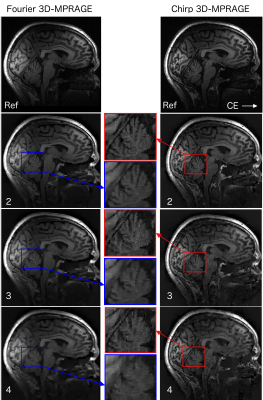
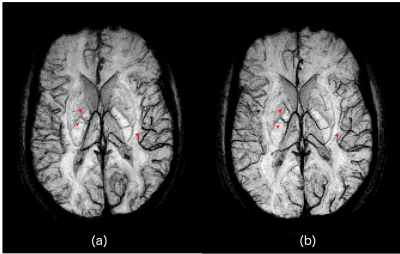
Fig.2 shows the simulation results for the acceleration factors of 4 and 6. It is evident form the enlarged images and line plot that chirp encoding is able to preserve the spatial resolution better than the Fourier encoding. Fig.3 shows the result of MCS reconstruction from the acquired in-vivo data that is consistent with the simulation results and shows improved resolution in the reconstructed images. Minimum intensity projection (mIP) across 20 axial slices from fully sampled GRE dataset is shown in Fig.4, highlighting that the veins are more prominent and sharper in the chirp-encoded mIP image.Discussion
The improved resolution in the chirp-encoded images can be attributed to the fact that chirp encoding spreads the energy in the measurement domain. A variable density under-sampling performed in the Fourier-encoded compressive sensing acquisition results in insufficient capture of high frequency components and hence a loss in resolution. However, for chirp encoding the energy is completely spread out in the measurement domain. A complete random under-sampling of chirp-encoded data results in the preservation of sufficient high frequency components and hence provides better resolution in the reconstructed images.Conclusion
An implementation of the chirp-encoded MRI is presented for the 3D GRE and MPRAGE sequences. The application of chirp encoding to CS and SWI demonstrates that chirp encoding outperforms Fourier encoding in preserving spatial resolution for anatomical scans and is an excellent candidate for accelerated imaging.Acknowledgements
No acknowledgement found.References
- Justin P Haldar, Diego Hernando, and Zhi-Pei Liang. Compressed-sensing MRI with random encoding. IEEE transactions on Medical Imaging, 30(4):893–903, 2011.
- Gilles Puy, Jose P Marques, Rolf Gruetter, Jean-Philippe Thiran, Dimitri Van De Ville, Pierre Vandergheynst, and Yves Wiaux. Spread spectrum magnetic resonance imaging. IEEE transactions on medical imaging, 1(3):586–598, 2012.
- Dong Liang, Guangwu Xu, Haifeng Wang, Kevin F King, Dan Xu, and Leslie Ying. Toeplitz random encoding MR imaging using compressed sensing. In Biomedical Imaging: From Nano to Macro, 2009. ISBI’09. IEEE International Symposium on, pages 270–273. IEEE, 2009.
- Kamlesh Pawar, Gary Egan, and Jingxin Zhang. Multichannel compressive sensing MRI using noiselet encoding. PloS one, 10(5):e0126386, 2015.
Figures