0361
Improving compressed sensing reconstructions for myocardial perfusion imaging with residual artifact learning1Radiology & Imaging Sciences, University of Utah, Salt lake city, UT, United States, 2US MR R&D Collaborations, Siemens Healthineers, Salt Lake City, UT, United States, 3Cardiology, University of Utah, Salt Lake City, UT, United States
Synopsis
Compressed sensing/constrained reconstruction methods have been successfully applied to myocardial perfusion imaging for improving in-plane resolution and improving slice coverage without losing temporal resolution.
Introduction
Myocardial perfusion MRI characterizes coronary artery disease by evaluating the impact of obstructed coronaries on myocardial tissue. There are multiple ways to perform perfusion MRI; for example, standard approaches use ECG-gated acquisitions with breath-holding while non-ECG gated or ungated acquisitions with free-breathing approaches are emerging. k-t space data undersampling with compressed sensing (CS) /constrained reconstructions are applied on conventional ECG-gated [1,2] as well as ungated acquisitions [3-5] for improving in-plane and slice resolutions without sacrificing temporal resolution. However, CS reconstructions can suffer from poor image quality when the data undersampling factor is too high and/or when there is large breathing or cardiac motion in the data. Here we use a deep learning framework to learn the residual artifacts from spatio-temporal constrained reconstructions (STCR) with total variation constraints [1,6,7]. Improved image quality is obtained by subtracting neural-network-predicted artifacts from the images reconstructed with STCR.Methods
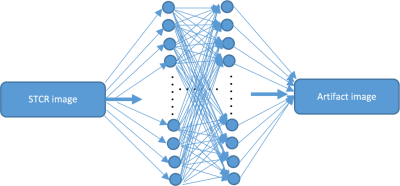
Two convolutional neural networks (CNNs) were trained separately on real and imaginary parts of the complex image data. Each CNN was 48 layers deep. Each convolutional layer (with 64 3x3 filters) was followed by a batch normalization layer [6] that was followed by a rectified linear unit layer [7], all repeating in that order. We used drop-out regularization to prevent overfitting to the training data [8]. Images from undersampled k-t space data after STCR were input to the network. The network was trained to learn the residual STCR artifacts obtained by subtracting ground-truth reconstructions from STCR images. Figure 1 shows an illustration of the proposed residual artifact learning framework.
We tested the above artifact learning (AL) framework on gated Cartesian [9] and ungated radial data [10] using separate training networks. STCR was done for each coil separately [1] for the Cartesian data. Joint multi-coil STCR reconstructions [11] were done for the radial data. ‘Truth’ images were obtained from (i) Inverse Fourier Transform reconstructions of fully sampled k-t space data for the Cartesian acquisitions and (ii) from 24-ray STCR for the radial acquisitions. STCR reconstructions from 21 phase encodes (R=4.5 with variable density undersampling for Cartesian data) and 8 radial rays were used as inputs to the training networks. All of the perfusion data were acquired on a Siemens 3T scanner. For the Cartesian acquisitions TR ranged from 140–175 ms, TE ranged from 0.98–1.36 ms, and slice thickness ranged from 7–8 mm [9]. All of the radial data with the golden ratio based angular spacing were acquired with identical scan parameters [10], TR=2.2 msec, TE=1.2 msec, slice thickness=8 mm. 40 x 40 spatial patches were extracted and training was done for 50 epochs on a system with two NVIDIA K80 GPUs which took ~48 hours. A total of 256 perfusion datasets (including slices, coils and stress and rest injections) from six patients were used for training the Cartesian network. For training the radial network 160 perfusion datasets from 10 patients were used. Datasets from two patients that were not used in training the CNNs were used for testing.
Results
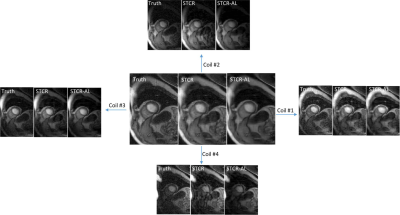
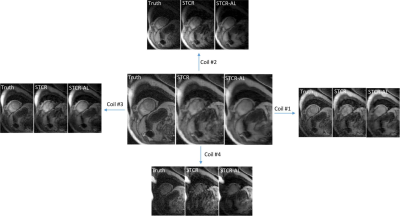
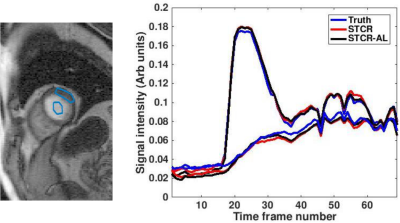
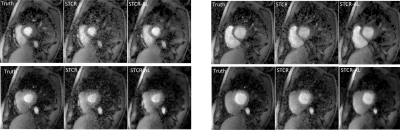
Figures 2a-2c show the results on a Cartesian dataset that was not used in training. Figure 2a shows one time frame post-contrast comparing the ‘Truth’, ‘STCR’ image that corresponds to reconstruction from R=4.5 data and ‘STCR-AL’ image that corresponds to the image from artifact learning framework. Sum-of-squares image and individual coil images are shown. Figure 2b shows another time frame from the same dataset with breathing motion in the neighboring time frames. STCR image quality is affected when there is inter-time-frame motion. STCR-AL images have fewer ghosting artifacts than STCR images. Figure 2c shows mean signal intensity time curves for regions of interest in the left ventricular blood pool and myocardium for the three reconstructions. Figure 3 shows the results on an ungated radial perfusion dataset that was not used in training. Images at near systole and near diastole at two different time points are shown. STCR-AL images have fewer pixelation artifacts than STCR images. The proposed network took ~7 msec to estimate artifacts in one image.Discussion and Conclusion
Residual artifact learning is promising for overcoming limitations of STCR for myocardial perfusion imaging. Here we trained the networks to learn the residual artifacts instead of the ‘True’ images as was done for improved image denoising [12]. We trained two networks on real and imaginary images instead of magnitude images as this gave improved results. Obtaining high-quality images from fewer samples robustly can improve temporal resolution and slice coverage that can potentially lead to improved sensitivity and specificity of myocardial perfusion imaging for detecting coronary artery disease. The proposed artifact-learning framework has the potential towards achieving this by overcoming limitations of CS methods.Acknowledgements
No acknowledgement found.References
[1] G. Adluru, C. McGann, P. Speier, E.G. Kholmovski, A. Shaaban, E.V. Dibella, Acquisition and reconstruction of undersampled radial data for myocardial perfusion magnetic resonance imaging, Journal of magnetic resonance imaging : JMRI, 29 (2009) 466-473.
[2] R. Otazo, D. Kim, L. Axel, D.K. Sodickson, Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI, Magn Reson Med, 64 (2010) 767-776.
[3] E.V.R. DiBella, L. Chen, M.C. Schabel, G. Adluru, C.J. McGann, Myocardial perfusion acquisition without magnetization preparation or gating, Magnetic Resonance in Medicine, 67 (2012) 609-613.
[4] A. Harrison, G. Adluru, K. Damal, A.M. Shaaban, B. Wilson, D. Kim, C. McGann, N.F. Marrouche, E.V. Dibella, Rapid ungated myocardial perfusion cardiovascular magnetic resonance: preliminary diagnostic accuracy, Journal of cardiovascular magnetic resonance : official journal of the Society for Cardiovascular Magnetic Resonance, 15 (2013) 26.
[5] B. Sharif, R. Dharmakumar, R. Arsanjani, L. Thomson, C.N. Bairey Merz, D.S. Berman, D. Li, Non–ECG-gated myocardial perfusion MRI using continuous magnetization-driven radial sampling, Magnetic Resonance in Medicine, 72 (2014) 1620-1628.
[6] S. Ioffe, C. Szegedy, Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, in: B. Francis, B. David (Eds.) Proceedings of the 32nd International Conference on Machine Learning, PMLR, Proceedings of Machine Learning Research, 2015, pp. 448--456.
[7] A. Krizhevsky, I. Sutskever, G.E. Hinton, ImageNet classification with deep convolutional neural networks, in: Proceedings of the 25th International Conference on Neural Information Processing Systems - Volume 1, Curran Associates Inc., Lake Tahoe, Nevada, 2012, pp. 1097-1105.
[8] N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever, R. Salakhutdinov, Dropout: a simple way to prevent neural networks from overfitting, J. Mach. Learn. Res., 15 (2014) 1929-1958.
[9] G. Adluru, S.P. Awate, T. Tasdizen, R.T. Whitaker, E.V. Dibella, Temporally constrained reconstruction of dynamic cardiac perfusion MRI, Magn Reson Med, 57 (2007) 1027-1036.
[10] D. Likhite, P. Suksaranjit, G. Adluru, N. Hu, C. Weng, E. Kholmovski, C. McGann, B. Wilson, E. DiBella, Interstudy repeatability of self-gated quantitative myocardial perfusion MRI, Journal of Magnetic Resonance Imaging, 43 (2016) 1369-1378.
[11] D. Likhite, G. Adluru, N. Hu, C. McGann, E. DiBella, Quantification of myocardial perfusion with self-gated cardiovascular magnetic resonance, Journal of Cardiovascular Magnetic Resonance, 17 (2015) 1-15.
[12] K. Zhang, W. Zuo, Y. Chen, D. Meng, L. Zhang, Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising, IEEE transactions on image processing : a publication of the IEEE Signal Processing Society, 26 (2017) 3142-3155.
Figures