0311

Acceleration of arterial spin labeling data acquisition using spatio-temporal total generalized variation (TGV) reconstruction
Stefan Manfred Spann1, Christoph Stefan Aigner1, Matthias Schloegl1, Andreas Lesch1, Kristian Bredies2, Stefan Ropele3, Daniela Pinter3, Lukas Pirpamer3, and Rudolf Stollberger1,4

1Institute of Medical Engineering, Graz University of Technology, Graz, Austria, 2Institute of Mathematics and Scientific Computing, University of Graz, Graz, Austria, 3Department of Neurology, Medical University of Graz, Graz, Austria, 4BioTechMed-Graz, Graz, Austria

Synopsis

3D imaging sequences such as GRASE or RARE-SoSP are the preferable choice for acquiring ASL images. However, a tradeoff between the number of segments and blurring in the images due to the T2 decay has to be chosen. In this study we propose a reconstruction algorithm based on total generalized variation for reducing the number of segments and therefore the acquisition time of one image. We incorporate the averaging procedure in the reconstruction process instead of reconstructing each image individually. This allows exploiting temporal redundancy and spatial similarity for improving the reconstruction quality of ASL images.

Introduction

In arterial spin labeling (ASL) 3D imaging sequences such as GRASE1 or RARE-SoSP2 are the preferable choice for acquiring perfusion weighted images (PWI), due to SNR-efficiency and efficient background suppression.3 However, the long readout-train leads to image-blurring accounted to T2 decay. An alternative procedure is based on acquiring more segments at the cost of prolonged acquisition times and an increased sensitivity to inter-segmentation motion. Different reconstruction algorithms were proposed which mainly focus on the reconstruction of each individual C/L image.4,5,6 In this study we used a modified CAIPIRINA7 sampling pattern in combination with a reconstruction algorithm based on total generalized variation8 to reduce the number of segments. Instead of reconstructing each image individually, the averaging procedure is incorporated in the reconstruction process. This allows the use of temporal redundancy and spatial similarity for improving the reconstruction quality of ASL images. Furthermore, for each average a different undersampling pattern is used which increases the incoherence of undersampling artifacts. The proposed algorithm was tested on synthetic and in-vivo data.

Methods

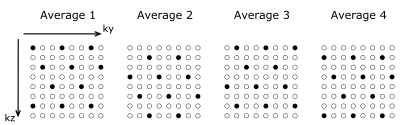
Four healthy volunteers were scanned at a 3T MR system (Prisma, Siemens Healthcare, Germany) using pseudo-continuous ASL labeling with a 3D GRASE readout.9 The following imaging parameters were used: matrix = 64x64x46, 46 slices with 10% slice oversampling, 3mm isotropic resolution, TR/TE=4000/16 ms, EPI-factor=21, TF=17, PLD=1800ms, 9 segments, 4 C/L-pairs resulting in an acquisition time of 4min 48s for the whole k-space. K-space data were retrospectively under sampled as illustrated in Figure 1, using 21 phase encodings in ky which corresponds to an EPI factor of 21. In slice direction every second line is acquired yielding two segments and a third additional segment covering the center of k-space is used for each average (21 central lines of the 17 central slices). For baseline evaluations a synthetic CBF-map was generated.10 Zero mean complex Gaussian noise was added to the C/L-raw-data. For the synthetic dataset 3D coil sensitivity profiles were simulated using Biot-Savart’s law. For in-vivo datasets coil sensitivity profiles were estimated using the method proposed by Walsh.11 The image reconstruction is done solving the following minimization problem using primal dual algorithm12:

$$\min_{u_c, u_l} \frac{\lambda_c}{2}\left\|(MFC\mathbf{1}u_c - U_c^{\delta})\right\|_2^2 + \frac{\lambda_l}{2}\left\|(MFC\mathbf{1}u_l - U_l^{\delta})\right\|_2^2 + \gamma_1(s)TGV_{\alpha1,\alpha0}(u_l) + \gamma_2(s)TGV_{\alpha1,\alpha0}(u_c - u_l)$$

where $$$u_c\,$$$and$$$\,u_l$$$ are the 3D reconstructions, $$$\lambda_c$$$ is the regularization parameter for the control data and set to 11, $$$\lambda_l$$$ is the regularization parameter for the label data and set to 15. The parameter s controls the weighting between the two TGV terms and is calculated as described in13, $$$ U_c^{\delta}\,$$$and$$$\,U_l^{\delta}$$$ are the acquired 4D C/L-images, $$$\alpha1\,$$$and$$$\,\alpha0\ $$$ are fixed model parameters.8 The $$$\mathbf{1}$$$-operator generates a number of identical copies of $$$u_c\,$$$and$$$\,u_l$$$ over the temporal dimension. $$$C$$$ are the coil sensitivity maps, $$$M$$$ is a mask containing the undersampling pattern and $$$F$$$ is the Fourier operator.

Results and Discussion

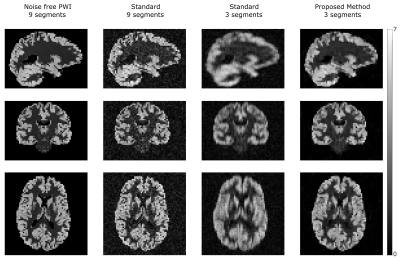
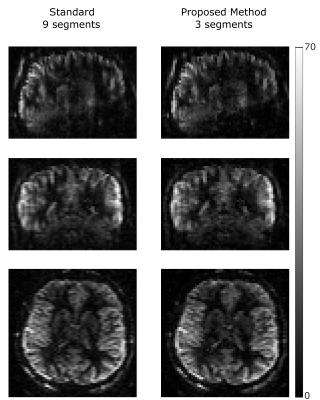
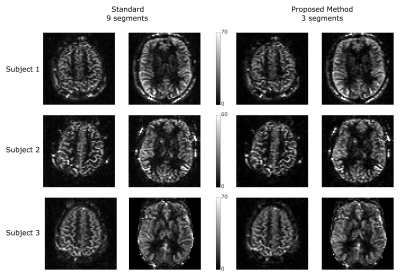
Figure 2 shows the synthetic PWI, the PWI using standard reconstruction with 9 and 3 segments and the PWI using the proposed reconstruction method with 3 segments of the k-space (undersampling factor US=3). Compared to the standard reconstruction the image quality can be increased using the proposed method and is in high accordance to the gold standard PWI. Figure 3 shows the reconstructed PWI from subject 4 using the fully sampled data acquired with 9 segments and the PWI reconstructed using the proposed algorithm with 3 segments (US=3). The image quality of the undersampled PWI is in high accordance with the fully sampled reference image. This is a result of varying the sampling-patterns for different averages which increases the incoherence which is then efficiently exploited by reconstructing the whole 4D dataset simultaneously. Figure 4 shows exemplary PWIs from 3 subjects using standard reconstruction from the fully sampled data and PWIs reconstructed from 3 segments using the proposed algorithm.

Conclusion

The performed study shows an effective way to accelerate the 3D-GRASE ASL acquisitions by increasing the incoherence with an adapted sampling strategy followed by a joint reconstruction of spatial and temporal dimensions. For 3mm isotropic data the number of segments can be reduced from 9 down to 3 which reduces the acquisition time for one image from 32s down to 12s and the total acquisition time from 4min 48s down to 1min 36s. The demonstrated approach can be easily adapted for alternative readout schemes like 3D EPI to reduce the number of phase encoding steps and mitigate EPI artifacts or RARE-SoSP to reduce the echo train length or the number of shots. Increasing spatial resolution, evaluation for stroke patients and the comparison to other reconstruction algorithms is subject to future work.

Acknowledgements

This work was funded by the Austrian Science Fund "SFB 3209-18".

NVIDIA Corporation Hardware grant support.

References

1. Guenther M, Oshio K, Feinberg DA. Single-shot 3D imaging techniques improve arterial spin labeling perfusion measurements. Magn. Reson. Med. 2005:54:491–498.

2. Vidorreta M, Wang Z, Rodríguez I, et al. Comparison of 2D and 3D single-shot ASL perfusion fMRI sequences. NeuroImage. 2013;0:662-671.

3. Alsop DC., Detre JA., Golay X, et al. Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: A consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magn. Reson. Med. 2015:73:102–116.

4. Shao X and Wang D JJ. Single shot high resolution 3D arterial spin labeling using 2D CAIPI and ESPIRiT reconstruction. Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

5. Ivanov D, Pfeuffer J, Gardumi A, et al. 2D CAIPIRINHA improves accelerated 3D GRASE ASL. Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

6. Chang YV, Vidorreta M, Wang Z, et al. 3D-accelerated, stack-of-spirals acquisitions and reconstruction of arterial spin labeling MRI. Magn Reson Med. 2017;78(4):1405-1419

7. Breuer FA, Blaimer M, Heidemann RM, et al. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med. 2005;53(3):684-91

8. Bredies K, Kunisch K, Pock T. Total Generalized Variation. SIAM J Imaging Sci. 2010;3(3):492-526.

9. Wang D JJ, Alger JR, Qiao JX, et al. The Value of Arterial Spin-Labeled Perfusion Imaging in Acute Ischemic Stroke – Comparison with Dynamic Susceptibility Contrast Enhanced MRI. Stroke; a Journal of Cerebral Circulation. 2012;43(4):1018-1024.

10. Bibic A, Knutsson L, Ståhlberg F, et al. Denoising of arterial spin labeling data: wavelet-domain filtering compared with Gaussian smoothing. MAGMA. 2010;23(3):125-137.

11. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med. 2000 May;43(5):682-90

12. Chambolle A, Pock T. A First-Order Primal-Dual Algorithm for Convex Problems with Applications to Imaging. J. Math. Imaging Vis. 2010;40:120–145.

13. Spann SM, Kazimierski KS, Aigner CS, et al. Spatio-temporal TGV denoising for ASL perfusion imaging. Neuroimage. 2017;157:81-96.

Figures

Figure 1: K-space acquisition pattern: The number of phase encodings ky is 21 which corresponds to an undersampling of 3 in phase direction. In slice direction each second line is acquired leading to two segments for the whole k-space. Additionally, for each average one segment is used to acquire the center of the k-space (21 central lines of the 17 central slices) resulting finally in 3 segments.

Figure 2: Synthetic generated PWIs, PWIs using standard reconstruction with 9 and 3 segments and PWIs reconstructed from 3 segments using the proposed algorithm. For reconstruction of all PWIs 4 averages are used.

Figure 3: Standard PWI reconstruction from one subject using the fully sampled data (9 segments) compared to PWI reconstructed using the proposed algorithm with 3 segments (US = 3).

Figure 4: Exemplary PWIs from 3 subjects using standard reconstruction from the fully sampled data (9 segments) compared to the proposed method with 3 segments.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0311