Synopsis

We investigate an optimization method for ASL fingerprinting acquisition schemes as well as a neural network framework for estimating hemodynamic parameters from the data.

Purpose

Multiple hemodynamic parameters can be estimated by applying fingerprinting techniques to arterial spin labeling (ASL) data [2]. The purpose of this work is to (1) optimize scan parameters for ASL MRF acquisition and (2) design a neural network regression framework for estimating multiple hemodynamic parameters.

We used the Cramer-Rao Bound (CRB) to construct a cost function for design optimization [3] and then used neural network regression techniques for parameter estimation to speed up the computations and reduce memory requirements by avoiding expensive dictionary-search based methods.

Methods

The CRB determines the lower bound on the variance of an unbiased estimator. It is defined as the inverse of the Fisher Information matrix, which is an indicator of the useful information contained in an observable random variable. It is a measure of the sensitivity of an observed signal to the underlying parameters describing the model for that signal. It can be written as: $$\begin{align}\mathbf{F}(\mathbf{\underline{\theta}};\mathbf{\underline{\nu}})&= \frac{1}{\sigma^2}\cdot[\nabla_{\mathbf{\underline{\theta}}}\mathbf{\underline{s}}]^T[\nabla_{\mathbf{\underline{\theta}}}\mathbf{\underline{s}}].\end{align}$$

Here, $$$\mathbf{\underline{s}}(\cdot)\in \mathbb{R}^{N\times 1}$$$ is the signal (N time frames) generated from our model, $$$\mathbf{\underline{\theta}}\in \mathbb{R}^{K\times 1}$$$ represents hemodynamic parameters of interest, $$$\mathbf{\underline{\nu}} \in \mathbb{R}^{P\times 1}$$$ are the scan parameter(s) and $$$\sigma^2$$$ is the i.i.d. additive Gaussian noise variance.

An ASL MRF sequence consists of a timeseries of labeling/control pulses followed by image acquisition. We optimized over the sequence of labeling durations by minimizing our CRB based cost function (akin to [1]), via exhaustive search. The optimization problem was formulated based on a normalized CRB as:$$\begin{align}\hat{\nu} = \underset{\nu \in \mathscr{V}}{\arg\min}~~\text{Tr}\bigg(W\cdot\frac{|F^{-1}(\mathbf{\underline{\theta}},\nu)|^{0.5}}{N}\cdot W\bigg),\end{align}$$ where $$$W$$$ is a diagonal weighting matrix assigning priority to each hemodynamic parameter in the cost function and $$$N = (\mathbf{\underline{\theta}}^{0.5})\cdot(\mathbf{\underline{\theta}}^{0.5})^T$$$ is a normalization matrix.

We investigated various timing schemes for the label order and duration to design an optimized ASL sequence for the two compartment model described in [2]: (i) Perlin function similar to that used in [2], (ii) Perlin function with one interpolation point (iii) cubic polynomial function (iv) time-reversed cubic polynomial. In the first case, the only adjustment was a scaling to ensure the scan time is 245 s. For the second case, we optimized the labeling duration at the interpolation point. In the final case, we optimized the polynomial coefficients. After optimization, we scaled the labeling schedule to ensure that all scans are 245 s long.

We used the optimized schedule to develop a neural network based regression framework to generate hemodynamic function estimates at each voxel. We designed two separate neural networks for estimating: (1) Perfusion alone, (2) Bolus Arrival Time (BAT) for tissue, Cerebral Blood Volume fraction(CBVa), and tissue R1 simultaneously.

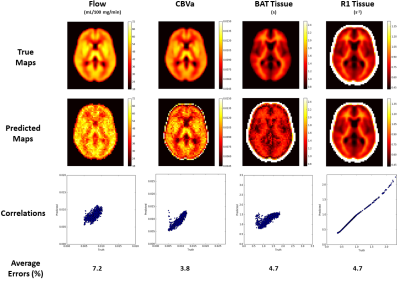
We trained these networks using the same dataset, consisting of 450K ASL MRF signals generated using the two-compartment model described in [2], plus noise. A $$$\pm 40 \%$$$ range around normative values for each parameter was used to generate the training data. Fig. 1 shows the neural network architectures investigated.

We tested the trained networks on new synthetic data generated using synthetic parameter maps to evaluate performance quantitatively. We used the NMAE and correlation between true and estimated parameters to evaluate performance.

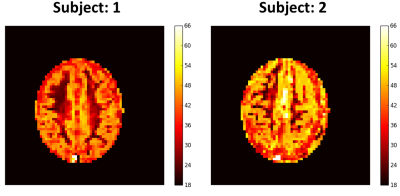
We then calculated perfusion maps from two healthy participants scanned using a truncated version of the above optimal ASL MRF scheme on a 3T MRI scanner with a 32 channel coil (MR750, GE, Waukesha, WI)

Results

The optimized 'reversed' cubic polynomial significantly improved the precision of estimating ASL parameters over other schemes (Fig. 2). Fig. 3 depicts the results for predicting parameter maps on a noisy synthetic data. The predicted maps have high fidelity with the ground truth over the training range, and have acceptably low average errors across the maps for all parameters. The estimation time for the depicted $$$55\times 46$$$ maps was 0.89 s for flow and 1.66 s for CBVa, BAT and tissue R1 on a NVIDIA Tesla K40c GPU, and required $$$\approx$$$ 10 Mb space to store each of the trained models. Fig. 4 depicts the estimated perfusion map for data collected on human subject based on the optimized tagging schedule.

Conclusion

Multiple hemodynamic parameter estimation from MRF ASL data is a promising powerful technique, but it is clear that it is challenged by computational demands and SNR constraints. Our preliminary results indicate that neural network regression is well suited for estimation of hemodynamic parameters from ASL MRF scans. Scan timing optimization using the Cramer Rao bound greatly improves the precision of the method. We were able to reduce computation time and memory requirements dramatically from [2].

Future work will involve validation and reliability testing. Other timing schemes will also be tested in silico and in vivo.

Acknowledgements

References

[1] Gopal Nataraj, Jon Fredrick Nielsen, and Jeffrey A. Fessler. Optimizing MR Scan Design for Model-Based T1, T2 Estimation from Steady-State Sequences. IEEE Transactions on Medical Imaging,PP(99):467–477, 2016.

[2] Pan Su, Deng Mao, Peiying Liu, Yang Li, Marco C. Pinho, Babu G. Welch, and Hanzhang Lu. Multiparametric estimation of brain hemodynamics with MR fingerprinting ASL. Magnetic Resonance inMedicine, 00(November):1–12, 2016.

[3] Anish Lahiri, Jeffrey A. Fessler, and Luis Hernandez-Garcia. Optimized Design of MRF Scan Parameters for ASL Signal Acquisition, ISMRM Workshop on Magnetic Resonance Fingerprinting. Poster #17. October 2017.