Synopsis

MR-STAT is a framework for obtaining multiple quantitative parameter maps from a very short scan. The parameter maps are obtained by fitting a Bloch-based signal model directly to the time domain data. No Fourier transform is needed. In this work we demonstrate that MR-STAT can obtain excellent high-resolution in-vivo quantitative maps using very short Cartesian acquisitions standardly available on clinical MR systems. The solution of the large-scale reconstruction problem is made possible by a highly parallelized, limited-memory algorithm.

Introduction

Methods

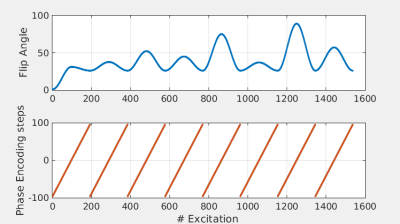
Acquisition: A 2D balanced gradient echo sequence, starting with an inversion pulse and followed by smoothly varying flip angles (max. 90 deg, see Figure 1) and 0-180 RF phase cycling was implemented on a 1.5T Philips Ingenia system. A single slice of gadolinium doped gel phantoms (Eurospin) and the brain of a healthy volunteer were scanned with a 15 channel receive head-coil. A Cartesian acquisition scheme was employed where the equivalent of 6 (in-vivo) and 8 (phantoms) k-spaces were filled in a linear fashion in ~6 seconds with a scan resolution of 1x1x5mm³. Inversion recovery and single spin echo experiments were performed on the gel phantoms to obtain gold standard T1 and T2 values. For the phantoms, the MR-STAT scan was repeated multiple times (with full relaxation in between) to study the effect of noise averaging.

Reconstruction: An iterative Gauss-Newton method was used. Because the number of parameters is vast, the approximated Hessian matrix cannot be stored. Therefore steps in parameter space are computed using a Conjugate Gradient Steihaug method,² which does not require the storage of the approximate-Hessian matrix. Parallelization is achieved over the spatial dimension (columns of the matrix are simultaneously evaluated). The algorithm is implemented on a computing cluster using the Julia programming language.³ Reconstruction time was ~15 minutes for the phantom data and ~1 hour for the in-vivo data using ~200 CPU cores.

Results

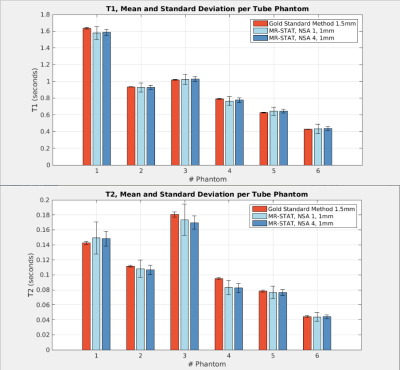
Phantoms: In Figure 2, the mean values and standard deviations of T1 and T2 per phantom tube obtained by MR-STAT and the gold standard methods are shown. The mean values are in close agreement. As expected, the standard deviation decreases with the square root of the number of scan averages.

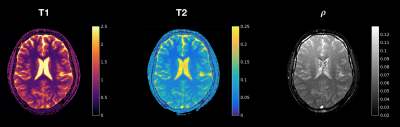
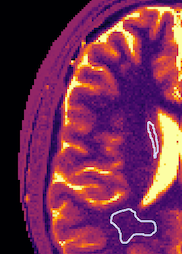
In-vivo: In Figure 3 the T1, T2 and proton density maps for the in-vivo scan are shown. Contrast between the different tissue types is clearly visible. In Figure 4, gray- and white matter regions are masked. The quantitative values in these regions are in line with literature values.⁴

Discussion

• In previous work,⁵ a 1D-FFT was exploited to decouple the large-scale MR-STAT reconstruction problem into multiple smaller problems to address the computational and memory requirements. In the current work, a more advanced reconstruction algorithm is developed instead to deal with these issues. The quality of the resulting parameters maps is significantly better compared to the previous results. Moreover, the current reconstruction allows for more freedom in the data acquisition (i.e. non-Cartesian trajectories).
• A relatively straightforward Cartesian acquisition scheme is employed because of its robustness against hardware imperfections (e.g. eddy currents). Non-Cartesian trajectories could be incorporated to boost scan efficiency. Furthermore, because MR-STAT does not rely on the Fourier transform, nonlinearity in gradients field can be incorporated in the reconstruction.
• Signals from different receive channels are combined using SVD compression. This combination does not necessarily lead to a uniform receive sensitivity, as can be observed in the proton density map and there is room for improvement here.
• Parallel imaging and regularization techniques could be exploited for additional acceleration and/or improved precision.
• Reconstructions are currently performed on a computing cluster. The reconstruction time decreases linearly with the number of cores used (as long as # cores < # voxels). Current work is focused on GPU implementation of the reconstruction code to further reduce reconstruction times and make MR-STAT more accessible.
• The long term goal of the MR-STAT project is to make 3D, sub-millimeter whole-brain quantitative parameter maps in less than 5 minutes of scan time. The matrix-free and highly parallelized reconstruction algorithm developed in this work is an important step towards that goal.

Conclusion

Acknowledgements

References

1. Sbrizzi A. et al, MRI 2017 (In-press), DOI: 10.1016/j.mri.2017.10.015

2. Nocedal J. & Wright S.J. - Numerical optimization, 2006, p. 171.

3. https://julialang.org/

4. Wright P.J. et al, MAGMA 2008, DOI: 10.1007/s10334-008-0104-8.

5. van der Heide O. et al, ISMRM 2017, p. 3962.

6. Kose R. et al, JMR 2017, DOI:10.1016/j.jmr.2017.05.007