Synopsis

Successful compressed-sensing reconstruction often involves tuning one or more regularization weights. However, tuning the regularization weights is a subject-specific, task-dependent and non-trivial task. Recent studies have proposed to determine the weights by minimizing the statistical risk of removing significant coefficients using line searches across a range of parameters. However, the line-search procedures lead to prolonged reconstruction times. Here, we propose a new self-tuning approach generalized for multi-coil, multi-acquisition CS reconstructions that leverage projection onto epigraph sets of l1 and TV balls. The proposed method yields 7 to 9-fold gain in computational efficiency over conventional methods while enabling further improved image quality.

Introduction

Compressed-sensing (CS) MRI improves scan efficiency by reconstructing from randomly undersampled k-space acquisitions¹. The reconstruction is often cast as a regularized optimization problem in which data-fidelity, transform-domain sparsity (e.g., via $$$l_1$$$-norm penalty) and denoising (e.g., via total-variation (TV) penalty) are simultaneously sought. Reconstruction quality heavily depends on the relative weighing of regularization terms against data fidelity. Unfortunately, tuning of regularization weights is a subject-specific and computationally-intensive task.

Recently, we reported a self-tuning approach (SPE) for parameter-free reconstruction of multiple-acquisition balanced steady-state free precession (bSSFP) data². The $$$l_1$$$-norm of wavelet coefficients and TV of the image were regularized. In-line with recent studies^3,4, both $$$l_1$$$ and TV weights were determined to minimize the statistical risk of removing significant coefficients using line searches across a range of parameters, which led to prolonged reconstruction times.

Here, we propose a new self-tuning approach generalized for multi-coil, multi-acquisition CS reconstructions named PESCaT (Projection onto Epigraph Sets for reconstruction by Calibration over Tensors). PESCaT leverages highly efficient geometric operations to determine the optimal regularization weights and apply them to the data. Phantom and in-vivo results are presented for several applications to demonstrate 7 to 9-fold gain in computational efficiency over SPE.

Methods

K-space data were variable-density randomly undersampled⁵. Unacquired data($$$\tilde{x}_{nd}$$$) were synthesized from acquired data ($$$y_{nd}$$$) via tensor interpolation across the acquisition (n) and coil (d) dimensions⁶:

$$\min_{\tilde{x}_{nd}}\{\sum_{n=1}^N\sum_{d=1}^D||(\mathcal{T-I})\tilde{x}_{nd}+(\mathcal{T-I})y_{nd}||_2^2+\sum_{n=1}^N\sum_{d=1}^D\lambda_{TV,nd}TV(m_{nd})^2+\sum_{i=1}^I\lambda_{l_1,i}||\sqrt{\sum_{n=1}^N\sum_{d=1}^D|\Psi_i(m_{nd})|^2}||_1^2\}~~~~(1)$$

where $$$m_{nd}$$$ is the reconstructed image for acquisition n and coil d,$$$\Psi_i$$$ is the wavelet operator at the ith level,$$$\mathcal{T}$$$ is the tensor interpolation operator,$$$\lambda_{TV,nd}$$$ is the TV-weight, and $$$\lambda_{l_1,i}$$$ is the $$$l_1$$$-weight.

The optimization problem was solved via an alternating projection-onto-sets scheme with calibration consistency, data-fidelity, joint $$$l_1$$$ and TV projections. Convergence was assumed when the percentage difference in MSE between images reconstructed in successive iterations fell below 20% in consecutive iterations. Calibration consistency was enforced using the tensor interpolation kernel⁴. Data fidelity was maintained by restoring acquired data. Proximal mapping was used to perform both $$$l_1$$$ and TV projections in the following form:

$$\min_{x\in\mathbf{R}^n}||x_0-x||_2^2 + \Phi(x)^2 \equiv \min_{x\in\mathbf{R}^n}\left|\left| \begin{bmatrix} x_0 \\ 0 \end{bmatrix} - \begin{bmatrix} x \\ \Phi(x) \end{bmatrix}\right|\right|_2^2~~~~(2)$$

where $$$x_0$$$ is the input (e.g., wavelet coeff. for $$$l_1$$$, image coeff. for TV), $$$x$$$ is the auxiliary variable, and $$$\Phi(.)$$$ is the $$$l_1$$$-norm operator or TV function. Here we propose to solve Eq.2 by identifying the closest vector $$$\begin{bmatrix} x^* & \Phi(x^*) \end{bmatrix}^T \in \mathbb{R}^{n+1}~to~\begin{bmatrix} x_0 & 0 \end{bmatrix}^T$$$. This solution is equivalent to projection of the vector$$$\begin{bmatrix} x_0 & 0 \end{bmatrix}^T$$$ onto the epigraph set (ES) $$$C_{\Phi}$$$ defined as^7,8:

$$C_{\Phi} = \{\bar{x}=\begin{bmatrix}x\\y\end{bmatrix}:y\ge\Phi(x)\}.~~~~(3)$$

Thus, regularization weight selection is transformed to the selection of a scale parameter $$$\beta$$$ for the ES $$$C_{\Phi'}=\{\bar{x}=\begin{bmatrix}x&y\end{bmatrix}^T:y\ge\beta\Phi(x)\}$$$. Recent studies have shown that the scaled ES formulation is remarkably robust against deviations in $$$\beta$$$.^7,8 The optimal $$$\beta$$$ was determined separately for $$$l_1$$$ and TV epigraphs using training data from a single reserved subject.

Demonstrations were performed based on brain phantom data simulated with a phase-cycled bSSFP sequence, and in-vivo brain data acquired with phase-cycled bSSFP, T1-weighted MP-RAGE, and time-of-flight (ToF) sequences. The following undersampling factors were examined: R=2, 4, 6 for bSSFP, R = 2, 4 for T1-weighted and ToF acquisitions. Reconstructions were obtained using PESCaT and SPE methods. Reconstructions were compared against fully sampled reference images to measure MSE and peak SNR (PSNR) metrics. To demonstrate the improvement in convergence behavior with PESCaT, the evolution of MSE between the reconstructed image at each iteration and the fully-sampled reference was measured.

Results

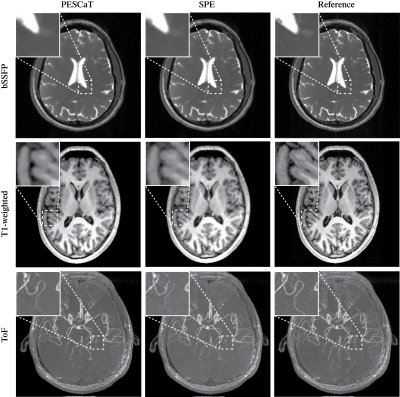
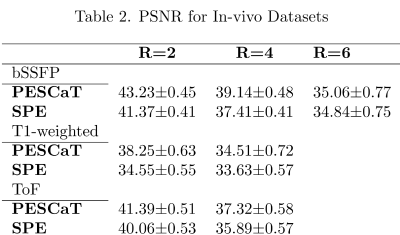
Fig.1 shows reconstructions and error maps for the phantom dataset. Fig.2 shows the reconstructions for in-vivo datasets. In both cases, PESCaT achieves superior tissue depiction with lower aliasing artifacts compared to SPE. These observations are supported by the PSNR measurements listed in Tables 1 and 2. On average, PESCaT improves the PSNR by 1.29±0.29dB in the phantom dataset and by 1.27±0.56dB, 2.29±0.61dB, and 1.38±0.54dB in the in-vivo bSSFP, T1-weighted, and ToF datasets (mean±std. across five cross-sections, average over all R).

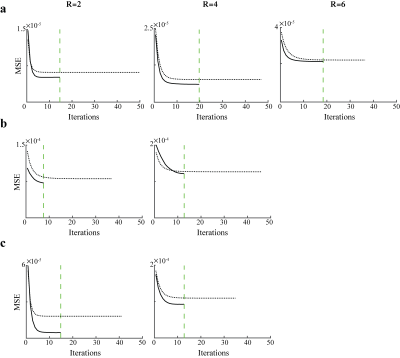
Fig.3 shows the convergence behavior of PESCaT versus SPE for in-vivo datasets. Compared to SPE, PESCaT converges in a notably lower number of iterations consistently across all datasets. Whereas SPE converges in 42.9±8.0 iterations each lasting 20.1±6.5s, PESCaT converges in only 14.2±3.4 iterations each taking 9.2±2.4s (mean±std. across datasets, average over five cross-sections and all R). Overall, PESCaT enables a 7-9 fold faster reconstruction compared to SPE.

Conclusion

Acknowledgements

References

1. Lustig, M., Donoho, D., and Pauly, J., “Sparse MRI: The application of compressed sensing for rapid MR imaging,” Magnetic Resonance in Medicine, vol. 58, no. 6, pp. 1182–1195, 2007.

2. Ilicak, R., Çukur, T., "Parameter-Free Profile Encoding Reconstruction for Multiple-Acquisition bSSFP Imaging." Proceedings of the 25th Annual Meeting of ISMRM, Honolulu. 2017

3. Weller, D.S., Ramani, S., Nielsen, J.F. and Fessler, J.A., 2014. Monte Carlo SURE‐based parameter selection for parallel magnetic resonance imaging reconstruction. Magnetic resonance in medicine, 71(5), pp.1760-1770.

4. Khare, K., Hardy, C.J., King, K.F., Turski, P.A., and Marinelli, L., 2012. Accelerated MR imaging using compressive sensing with no free parameters. Magnetic resonance in medicine, 68(5), pp.1450-1457.

5. Çukur, T., “Accelerated Phase-Cycled SSFP Imaging with Compressed Sensing,” IEEE Transactions on Medical Imaging, 2015.

6. Biyik, E., Ilicak, E., and Çukur, T., “Reconstruction by calibration over tensors for multi‐coil multi‐acquisition balanced SSFP imaging,” Magnetic resonance in medicine, 2017.

7. Cetin, A.E., and Tofighi, M., “Projection-based wavelet denoising [lecture notes],” IEEE Signal Processing Magazine, 2015.

8. Tofighi, M., Kose, K., and Cetin, A.E., “Denoising images corrupted by impulsive noise using projections onto the epigraph set of the total variation function (PES-TV),” Signal, Image and Video Processing, vol. 9, no. S1, pp. 41–48, 2015.