0250
Complex Image Extraction in Phased-Array Imaging1Radiology and Biomedical Imaging, University of California, San Francisco, San Francisco, CA, United States
Synopsis
Phased-array coils are used in MRI to improve signal-to-noise ratio (SNR) or to accelerate data acquisition speed through parallel imaging. It is beneficial to have a phased-array imagery reconstruction method that extracts the complex magnetization information from the multichannel data. In this work, we adopt the fusion frame theory to estimate the magnitude of the underlying magnetization and further employ the matched-filter method to estimate the magnetization phase, thereby reconstructing a complex image that does not have coil sensitivity weightings.
Introduction
Phased-array coils are used in MRI to improve signal-to-noise ratio (SNR) or to accelerate data acquisition speed through parallel imaging. In both schemes, final images are generally reconstructed either by performing the optimal coil combination method1,2 using the complex coil sensitivities or by taking the square root of the sum of squares (SSOS) of individual channel images. In practice, accurate sensitivity profiles are hard to achieve and any miscalibration manifests as artifacts in the final image. The SSOS method is easy to implement but suffers from coil weightings in the final image and hence hinders quantitative magnetization estimation. Furthermore, no phase information can be retrieved. Therefore, it is beneficial to have a phased-array imagery reconstruction method that extracts the complex magnetization information from multichannel data. In this work, we adopt the fusion frame theory3 to estimate the magnitude of the underlying magnetization and further employ the matched-filter method4 to estimate the magnetization phase, thereby reconstructing a complex image that does not have coil sensitivity weightings.Methods
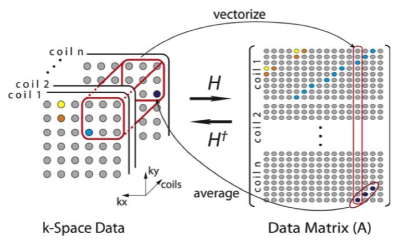
Complex image estimation from multichannel data was done through the following. First, multichannel data were structured into a data matrix (A) as shown in Figure 1. Then the matrix A was decomposed into A=UΣVH using the singular-value decomposition (SVD). The dominant singular vectors in U were used to generate the spatial matched filters and to estimate the phase as described in Uecker et al.5 The dominant singular vectors in V were used to generate a fusion frame and its associated fusion frame operator (S). It can be shown that the impulse response of S is the weighted Fourier transform of the squared magnitude of the magnetization. Therefore, the desired magnitude image can be estimated from $$\mid I \mid =\sqrt{F^{-1}W^{-1}S(\delta)},$$ where F is the Fourier transform, W is the weighting matrix and I is the image.
To demonstrate the capability of the proposed method, we performed the following experiments. First, we used a T1-weighted, IR-SPGR 8-channel brain data and reconstructed final images using SSOS and the proposed method. To show the removal of coil weighting, plots of the magnitude values along a line in the images were also calculated. Next, using the same data, we removed three coil data (channels 6,7, and 8 placed at the upper-left corner of the brain) and again reconstructed using SSOS and the proposed method. Finally, we performed the same experiment using a T2-weighted, fat-suppressed 8-channel knee data. After noticing a singularity in the phase image, we removed a coupled coil data and reconstructed again to compare the results.
Results
Figure 2 shows the results from the SSOS and the proposed reconstruction with the phase image. Note the bright subcutaneous fat signal surrounding the cranium, which is a characteristic of the used T1-weighted IR-SPGR sequence. The magnitude image acquired from the proposed method shows evenly distributed fat signals, whereas the SSOS image clearly shows the effect of coil weighting.
Figure 3 shows reconstructed results from using only a subset of coils. The SSOS image shows severe darkening in the area where the removed three coils were originally placed. As opposed to that, the proposed method is able to reconstruct all the structures in that area with slightly decreased SNR.
Figure 4 shows the same set of experiment performed with the knee data. The magnitude image from the proposed method again shows flat magnetization profile compared to the SSOS image. However, the phase image contained a singularity. This phenomenon has been observed consistently in works that adopted adaptive coil combination method6.
After noticing the singularity, we looked through individual coil images and identified a channel that suffered from coupling. We then removed the coil data and reconstructed again with the proposed method. Figure 5 shows the coupled coil and the reconstructed magnitude and phase images. Once the coupled coil data was removed, we were able to estimate the phase better with minimally decreased SNR in the magnitude image.
Discussion
By forming a fusion frame using the dominant singular vectors, we were able to stably estimate the magnitude of the underlying magnetization that does not suffer from coil weighting. The proposed method also shows robustness to removal of coil data because it estimates the magnetization information, which is redundantly shared among different coils. Estimating the phase information needs further improvement as the used adaptive scheme can generate phase singularities.Conclusion
We have presented a phased-array reconstruction method that extracts complex magnetization images that does not contain coil weightings as in SSOS. The proposed method can be valuable in applications where magnetization quantification is crucial.
Acknowledgements
We gratefully acknowledge National Institutes of Health (P41-EB013598) for their financial support.
References
1. Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med 1990;16:192–225.
2. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42:952–962.
3. Casazza PG, Kutyniok G, Li S. Fusion frames and distributed processing. Appl Comput Harmon Anal 2008;25:114-132.
4. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med 2000;43:682–690.
5. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT—an eigenvalue approach to auto- calibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71:990–1001.
6. Inati SJ, Hansen MS, Kellman P. A solution to the phase problem in adaptive coil combination. Proc Intl Soc Mag Reson Med 2013;21:2672.
Figures
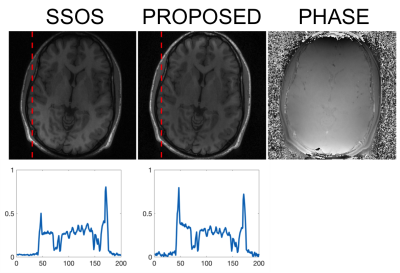
Final images reconstructed using the SSOS method and the proposed method. The phase image is also shown. Note that the SSOS image suffers from severe coil weighting especially towards the bottom of the image, whereas the proposed image shows a flat profile. The magnitude plots correspond to the red dotted lines. Both the magnitude images were normalized to the same scale. The image size is 200 x 200.
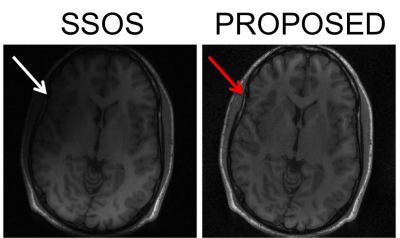
Reconstructed results with three coils removed. Note the darkening in the SSOS image (white arrow) around the area where the removed three coils were originally placed. On the contrary, the image from the proposed method maintained all of the image structure with slight penalty in SNR (red arrow).
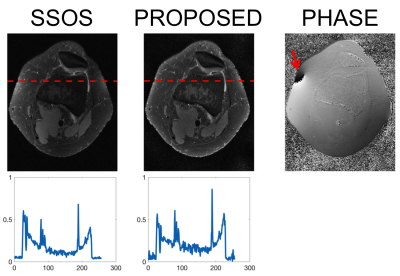
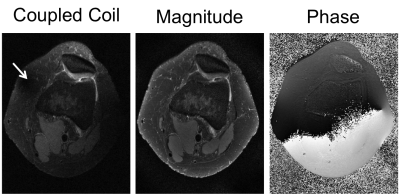
Phase image correction by removing coupled coils. One of the channel showed severe coupling to its neighboring coils (white arrow). By removing the coupled channel, we were able to stably estimate the magnitude and the phase.