0243
Kernel low-rank regularization: an efficient approach for recovering dynamic images on a manifold1University of Iowa, Iowa City, IA, United States
Synopsis
The main focus of this abstract is to introduce an efficient algorithm to recover a free breathing and ungated cardiac MR image series from highly undersampled measurements. The main contributions are (i) a kernel low-rank algorithm to estimate the manifold structure (Laplacian) from noisy navigator signals, (ii) a fast algorithm that uses the Laplacian basis functions to recover the data from highly undersampled measurements. The utility of the algorithm is demonstrated on radial acquisitions from patients with congenital heart disease; the results show that the framework is a promising alternative to self-gating methods.
Introduction
Self-gated acquisition strategies are emerging as promising alternatives to breath-held cardiac MRI protocols, especially for patients who cannot hold their breath such as pediatric patients or developmentally delayed adults. Current self-gating methods rely on complex steps (involving bandpass filtering and non-linear processing) to estimate the cardiac and respiratory information and use it to bin and recover the data1. We2 and others3,4 have introduced an alternate strategies which model the images as points on a manifold. Our approach (SToRM) estimates the manifold Laplacian from navigators using a Gaussian kernel. Since the performance of the algorithm is critically dependent on the manifold structure, we introduce a novel kernel low-rank strategy to estimate the Laplacian reliably from noisy navigator data. We also introduce a fast algorithm that relies on the eigen functions of the Laplacian, and provides an order of magnitude reduction in computational complexity and memory demand. These developments make the SToRM framework considerably more suitable for clinical problems.Methods
We consider the recovery of $$$\mathbf X$$$, whose columns are images in the series. We estimate the manifold structure from the navigators $$$\mathbf Q= \boldsymbol \Phi \mathbf X$$$, where $$$\boldsymbol\Phi$$$ is the navigator acquisition operator. Our recent work shows that the non-linearly transformed original points $$$\boldsymbol\Psi(\mathbf q_i);i=1,..,N$$$ live in a subspace, if the original points $$$\mathbf q_i$$$ live on a band-limited surface. We consider the denoising of the navigator lines using the algorithm:\begin{equation}\mathbf Z^* = \arg\min_{\mathbf Z} \lbrace \|\mathbf Z - \mathbf Q\|_F^2 + \lambda~\|\mathbf \Psi(\mathbf Z)\|_* \rbrace,\end{equation}where $$$\mathbf \Psi(\mathbf Z)$$$ is the matrix whose columns are non-linear transforms of the original points and $$$\|\cdot\|_*$$$ denotes the nuclear norm. The kernel trick $$$\langle \mathbf \Psi(\mathbf x_1),\mathbf \Psi(\mathbf x_2)\rangle = \mathcal K(\mathbf x_1,\mathbf x_2)$$$, where $$$\mathcal K$$$ is the Gaussian kernel, allows us to solve the above problem using an iterative reweighted algorithm without performing the explicit mapping. In contrast, Nakarmi et al5 recently proposed a kernel low-rank technique, which requires computing the explicit images and pre-images. We solve the problem:\begin{equation}\mathbf Z^{(n)} = \arg\min_{\mathbf Z} \left\lbrace \|\mathbf Z - \mathbf Q\|_F^2 + \lambda~{\rm trace}\left(\mathbf Z~ \mathbf L^{(n)} ~\mathbf Z^{H} \right) \right\rbrace,\end{equation}where $$$\mathbf L^{(n)} = \mathbf D^{(n)} - \mathbf W^{(n)}$$$, $$$\mathbf W^{(n)} = \mathcal K(\mathbf Z^{(n-1)})\odot\mathbf P^{(n)}$$$, $$$\mathbf D^{(n)}_{ii} = \sum_j \mathbf W^{(n)}_{ij}$$$, and $$$\mathbf P^{(n)} = [\mathcal K(\mathbf Z^{(n-1)}) + \gamma^{(n)} \mathbf I]^{-\frac{1}{2}}$$$. This iterative algorithm is analogous to SToRM2, where $$$\mathbf L^{(n)}$$$ is the Laplacian. Thus, the above algorithm provides a robust estimate for the Laplacian as a by-product; we propose to use this $$$\mathbf L$$$ in SToRM to recover $$$\mathbf X$$$:\begin{equation}\mathbf X^* = \arg\min_{\mathbf X} \left\lbrace \|\mathcal{A}(\mathbf X) - \mathbf B\|_F^2 + \lambda~{\rm trace}\left(\mathbf X \mathbf L \mathbf X^{H} \right) \right\rbrace,\end{equation}where $$$\mathcal A$$$ is the measurement operator and $$$\mathbf B$$$ are the measurements. To reduce the computational complexity, we perform an eigen decomposition of $$$\mathbf L=\mathbf V \boldsymbol \Sigma \mathbf V^T$$$. The eigen functions are analogous to Fourier exponentials and are ideally suited to represent smooth functions on the manifold; this allows us to rewrite the above expression as:\begin{equation}\mathbf U^{*} =\arg \min_{\mathbf U} \|\mathcal A(\mathbf U\mathbf V^H)-\mathbf b\|^{2}_{F} + \lambda~ \sum_{i=1}^k \sigma_i \|\mathbf u_i\|^2\end{equation}Our experiments show that only $$$30$$$ basis functions are sufficient, which greatly reduces the computational complexity. The proposed scheme is summarized in Fig 1. Denoising of data using the proposed iterative kernel low-rank technique is illustrated in Fig 2.
Results
We demonstrate our scheme on 3 free-breathing ungated datasets acquired using a FLASH sequence on a Siemens 3T Aera scanner at the University of Iowa Hospitals and Clinics. The datasets were acquired using 10 radial lines per frame out of which 4 were navigators. The sequence parameters were: TR/TE 4.68/2.1 ms, FOV 300mm, Base resolution 256. 10000 spokes of k-space were collected in 47s. Fig 3 illustrates the reconstruction of a dataset using SToRM as well as the proposed technique. It is shown that the proposed technique recovers images of better quality and is also less computationally intensive. Fig 4 shows the performance of the proposed technique on a dataset with extensive breathing motion. Fig 5 demonstrates that the recovered ungated image series can easily be sorted into cardiac and respiratory phases using the eigen-vectors of the estimated Laplacian. A few representative images in different phases have been shown.Conclusion
The representation of the image data using a few basis images results in a computationally efficient algorithm. Moreover, the strategy of estimating the Laplacian by solving an optimization problem is shown to give better results than the heuristic technique of using exponential weights. These innovations result in high quality cardiac images in the free-breathing and ungated mode and provide an efficient method of performing cardiac MRI even in patients with complex congenital heart diseases.Acknowledgements
This work is supported by NIH 1R01EB019961-01A1.References
1. Li Feng, Leon Axel, Hersh Chandarana, Kai Tobias Block, Daniel K. Sodickson, Ricardo Otazo. XD-GRASP: Golden-Angle Radial MRI with Reconstruction of Extra Motion-State Dimensions Using Compressed Sensing. Magnetic Resonance in Medicine. 2016; 75(2): 775–788.
2. Sunrita Poddar, Mathews Jacob. Dynamic MRI using smoothness regularization on manifolds (SToRM). IEEE Transactions on Medical Imaging. 2016; 35(4):1106 - 1115.
3. M. Usman, D. Atkinson, C. Kolbitsch, T. Schaeffter, C. Prieto. Manifold learning based ECG-free free-breathing cardiac CINE MRI. Journal of Magnetic Resonance Imaging. 2015; 41(6):1521–1527.
4. Kanwal K. Bhatia, Jose Caballero, Anthony N. Price, Ying Sun, Jo V. Hajnal, Daniel Rueckert. Fast Reconstruction of Accelerated Dynamic MRI Using Manifold Kernel Regression. International Conference on Medical Image Computing and Computer-Assisted Intervention 2015.
5. Ukash Nakarmi, Yanhua Wang, Jingyuan Lyu, Dong Liang, Leslie Ying. A Kernel-based Low-rank (KLR) Model for Low-dimensional Manifold Recovery in Highly Accelerated Dynamic MRI. IEEE Transactions on Medical Imaging. 2017; 36(11): 2297 - 2307.
Figures
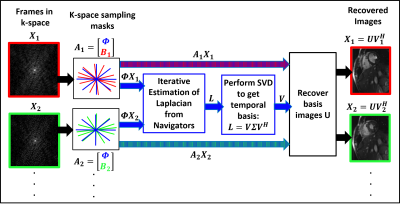
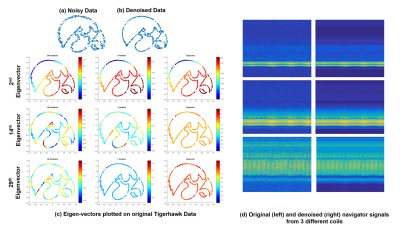
Illustration of denoising and Laplacian estimation using kernel low-rank algorithm. Noisy points on a TigerHawk logo in (a) are denoised using the algorithm to obtain (b). (c) shows the eigen-vectors of the Laplacian matrix estimated using $$$50^{th}$$$ iteration (left), $$$1^{st}$$$ iteration (center) and exponential approach (right), respectively. The higher order basis functions estimated by the proposed scheme are smooth and reliable, while the ones estimated using Exponential approach and from the first iteration are rough/not reliable.
We show the denoising of the navigator signals from three coils in (3). The Laplacian estimation from the denoised data provides improved results as shown in the next figure.
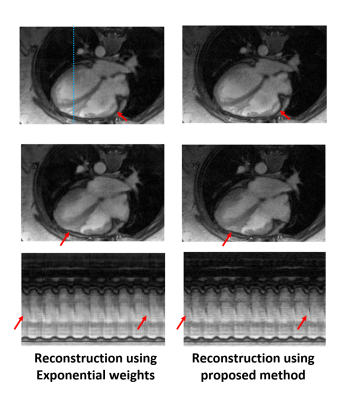
We compare the images reconstructed using the new approach (right column) and our previous STORM reconstruction (left column). The improved estimation of the Laplacian, along with the reconstruction using the temporal basis functions, translated to higher quality reconstructions. Specifically, the images reconstructed using the proposed technique look sharper and preserve the details much better. This can also be observed from the temporal profiles shown along the blue dotted line.
The use of the basis function based approach provided a significant speedup; the original SToRM reconstruction took around 30 mins, while the proposed reconstruction took only 2 mins.

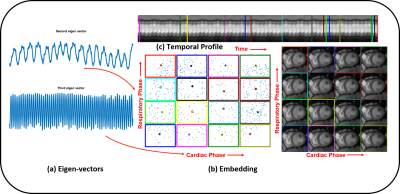
Manifold embedding of the images using the eigen vectors of the Laplacian matrix. The second and third eigen vectors in (a) provide information about the respiratory and cardiac phases, which can be used to segment the data into different phases. (b) shows the embedding of the images in the 2d plane. The images corresponding to the dots in the center of the colored squares (representative image with a specific cardiac and respiratory phase) are shown on the left. Note from (c) that these images actually come from different time points in the time series with 900 images.