0219
Time-optimal control based RF pulse design under gradient imperfections1Institute of Medical Engineering, Graz University of Technology, Graz, Austria, 2Institute for Mathematics and Scientific Computing, University of Graz, Graz, Austria, 3Division of Imaging Sciences and Biomedical Engineering, King's College London, London, United Kingdom, 4Johann Radon Institute for Computational and Applied Mathematics (RICAM), Austrian Academy of Sciences, Linz, Austria
Synopsis
We demonstrate the joint design of minimum duration RF and slice selective gradient shapes with included gradient impulse response function (GIRF) to correct for non-ideal slice selective gradients in the pulse design. The proposed time-optimal control method designs slice selective gradient shapes with matched RF shapes for the distorted slice selective gradient. Phantom experiments on a 3T scanner validate the optimized results and demonstrate the successful correction of gradient imperfections with the proposed approach.
Purpose
Joint design of minimum duration RF and slice selective gradient (Gs) shapes by time-optimal control1 for Simultaneous Multislice (SMS)2 refocusing can reduce the pulse length significantly3. Optimal solutions fully exploit the prescribed inequality constraints (slice profile accuracy, amplitude and phase constraints), which tends to produce strongly varying Gs shapes3. This might prevent the practical application of such optimized pulses due to gradient imperfections caused by eddy currents or time delays, which alter the oscillating Gs shapes. The gradient performance can be modeled by the time-invariant gradient impulse response function (GIRF)4 and its effect can be iteratively corrected for a given RF and Gs shape5. In this work, we show that a direct inclusion of the GIRF in a time optimal control framework1 allows to design short RF and Gs shapes for SMS refocusing that inherently corrects for non-ideal gradients.Theory
A time optimal control framework to jointly design the RF and Gs shape based on the Bloch spin domain formulation of a perfectly crushed spin echo $$$|b(z)|^2$$$ is introduced. The effects of the GIRF are modeled by a convolution in the time domain $$Gs_{GIRF}(t)= Gs(t)*GIRF(t).$$ Amplitude constraints for RF, Gs and Gs slew rate (for $$$Gs(t)$$$) and a global RF power constraint are prescribed. The Bloch simulations and slice profile constraints (magnitude and phase) are based on the filtered GsGIRF. We apply projection-based techniques (semismooth Newton) for the box constraints of the controls, and penalty techniques for the more general constraints. Adjoint-based exact first derivatives are formed via the Lagrangian, the second derivatives are supplied by a quasi-Newton (BFGS)6 algorithm. The free terminal time is optimized with the bilevel method for time-optimal control of our preceding work1.Methods
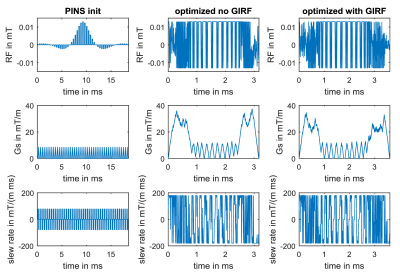
The iterative optimization started with a PINS7 RF and slice selective gradient shape based on a SLR8 sub-pulse. An example with five slices and real-valued RF pulses is presented. The maximal allowed error deviation of the individual refocused slices (thickness=2mm, time-bandwidth-product=4, slice-gap=24mm) from ideal refocusing was set to pointwise 2% (out-of-slice) and 3% (in-slice). The discretization used a spatial domain of 120mm with 2401 spatial points and a temporal discretization of 6.4µs. The constraints were B1max=13µT, Gsmax=39mT/m and slew ratemax=180mT/m/ms, respectively. The GIRF(t) was measured for a longitudinal (z-) gradient for a Philips Achieva 3T system using an image-based procedure. The proposed algorithm is implemented in MATLAB (The MathWorks, Inc, Natick, USA) and the calculations are done in parallel (OpenMP) using 16 cores and 128GB of RAM (Radon1, RICAM, Linz, Austria). The designed refocusing pulses were validated on a phantom by measuring refocusing profiles in a spin-echo sequence, using conventional MB excitation pulses with matching slice profiles. Experiments were conducted on the same system and gradient axis for which the GIRF was measured.Results and Discussion
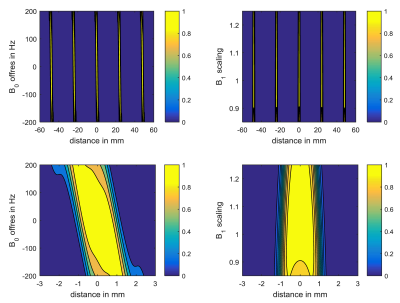
Figure 1 shows the PINS initial (left) together with the optimized results using no GIRF (middle) and the measured GIRF (right). The overall duration of the optimized results is reduced from 18.58ms to 3.17ms and 3.6ms, i.e. the inclusion of the measured GIRF in the optimization increases the optimized pulse duration only slightly and the optimized shapes of RF and Gs remain similar. Both, the RF amplitude and the slew rate of Gs meet the prescribed constraints. Figure 2 shows Gs and GsGIRF with and without inclusion of the GIRF into the optimization. Depicted are also the simulated refocusing profiles with and without GIRF. Gradient imperfections associated with high frequency components result in distorted slice profiles, most noticeable in the outer slices of the pack. The inclusion of the measured GIRF in the optimization however, completely corrects for these unwanted slice profile distortions and yields distinct refocusing slices across the field of view. While the optimizer generates a pre-emphasized Gs shape with frequency components outside the available amplifier bandwidth, the RF pulse and GsGIRF shape are matched to yield precise slice profiles. Figure 3 shows the refocusing profile for a B0 offset range of ±200Hz (left side) and a B1 variation of 85-125% for the GIRF optimized RF pulse and GsGIRF shown in Figure 2. These robustness properties agree with those of minimum-duration pulses without GIRF1. Figure 4 shows the reconstructed phantom measurements using the optimized RF and Gs shapes shown in Figure 1. As can be seen, the inclusion of the GIRF in the optimization clearly improves the refocused slice profile.Conclusion
The inclusion of a hardware specific GIRF into the optimal control framework allows to compensate for the gradient imperfections and achieve distinct refocusing slices, even for minimum-duration RF and Gs shapes.Acknowledgements
Partly supported by the Austrian Science Fund (FWF): SFB F3209-18 and BioTechMed-Graz. Samy Abo Seada is funded by the King’s College London & Imperial College London EPSRC Centre for Doctoral Training in Medical Imaging (EP/L015226/1).References
1) Rund A, Aigner CS, Kunisch K and Stollberger R. Simultaneous multislice refocusing by time-optimal control. Proc. Intl. Soc. Mag. Reson. Med. 25, 0522, Honolulu, Hawai'i, USA, 2017.
2) Barth M, Breuer F, Koopmans PJ, Norris DG and Poser BA. Simultaneous multislice (SMS) imaging techniques. Magn. Reson. Med. 75(1):63–81, 2016.
3) Grissom WA, Setsompop K, Hurley SA, Tsao J, Velikina JV and Samsonov AA. Advancing RF pulse design using an open-competition format: Report from the 2015 ISMRM challenge. Magn. Reson. Med. 78(4):1352–1361, 2016.
4) Vannesjo SJ, Haeberlin M, Kasper L, Pavan M, Wilm BJ, Barmet C, Pruessmann KP. Gradient system characterization by impulse response measurements with a dynamic field camera. Magn. Reson. Med. 69(2):583–593, 2013.
5) Abo Seada S, Hajnal J, and Malik S. A simple optimization approach to making time efficient VERSE-multiband pulses feasible on non-ideal gradients. Proc. Intl. Soc. Mag. Reson. Med. 25, 5049, Honolulu, Hawai'i, USA, 2017.
6) Nocedal J and Wright SJ. Numerical Optimization. Springer Series in Operations Research and Financial Engineering, Mikosch TV, Resnick SI, and Robinson SM, Eds. New York: Springer, 2nd edition, 2006.
7) Norris DG, Koopmans PJ, Boyacioglu R and Barth M. Power Independent of Number of Slices (PINS) radiofrequency pulses for low-power simultaneous multislice excitation. Magn. Reson. Med. 66(5):1234–1240, 2011.
8) Pauly J, Le Roux P, Nishimura D, and Macovski A. Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm. IEEE Trans. Med. Imaging 10(1), 1991.
Figures