0211

Accelerated T2-Weighted Imaging of the Abdomen with Self-Calibrating Wave-Encoded 3D Fast Spin Echo Sequences
Feiyu Chen1, Valentina Taviani2, Joseph Y. Cheng3, John M. Pauly1, and Shreyas S. Vasanawala3

1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Global MR Applications and Workflow, GE Healthcare, Menlo Park, CA, United States, 3Radiology, Stanford University, Stanford, CA, United States

Synopsis

In this work, a self-calibrating wave-encoded 3D FSE technique was proposed with self-refocusing gradient waveforms and autocalibrated estimation of wave-encoding point-spread-function and coil sensitivity maps. Compared to conventional Cartesian approach at the same acceleration factor, the proposed method achieves reduced artifacts and better anatomical delineation for highly undersampled abdominal imaging. It enables 10-fold acceleration for 3D FSE scans of the abdomen, allowing 3D FSE sequences to be less sensitive to subject motion.

Introduction

3D fast spin echo (FSE) imaging with variable refocusing flip angles (CUBE/SPACE/VISTA) enables isotropic imaging with high spatial resolution and high signal-to-noise ratio (SNR). However, compared to 2D fast imaging techniques1, 3D FSE is more sensitive to motion, as acquiring a 3D k-space usually takes a long time (~2-5min), even if state-of-the-art compressed sensing and parallel imaging reconstruction techniques are used. Therefore, it is desirable to further accelerate 3D FSE sequences to improve motion robustness, especially for abdominal imaging. Recently, wave encoding2 has been demonstrated to further accelerate MRI by exploiting coil sensitivity variations in both phase-encoding (PE) and frequency-encoding (FE) directions. Nonetheless, additional calibration scans of wave-encoding point-spread function (PSF) are usually necessary for variable-density undersampling3,4. In this work, we propose a self-calibrating wave-encoded 3D FSE technique, which achieves reduced artifacts and better anatomical delineation than standard Cartesian sequences for highly undersampled abdominal imaging.

Methods

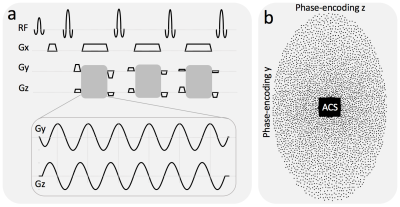
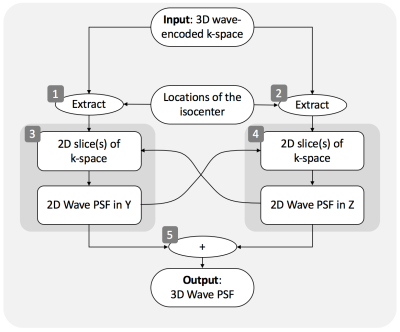
Self-refocusing wave-encoding gradients with 6 cycles/readout and 9.0 mT/m amplitude were designed to ensure refocusing of the k-space signal at the center of the calibration region in both phase-encoding directions (y, z) by reducing the area of the first and last Gy gradient lobes by 50% (Fig. 1a). A variable-density poisson-disk under-sampling pattern was introduced to reduce the number of acquired readouts by a factor of 10 (Fig. 1b). A 24×32 fully sampled calibration region was used for self-calibration of the wave-encoding PSF and coil sensitivity estimation. The wave-encoding PSF was calibrated in both phase-encoding directions based on the under-sampled wave-encoded k-space5 (Fig. 2). Self-calibration of the wave-encoding PSF was developed by maximizing the square of the normalized image gradient iteratively5,6. Auto-calibrated estimation of coil sensitivity maps7 using ESPIRiT8, and CS-SENSE image reconstruction9 with L1-wavelet regularization were performed using a combination of Python and C++ (BART toolbox10).

g-Factor maps of wave-encoded and Cartesian acquisitions were estimated theoretically for uniform under-sampling of 3 (PE in y) × 2 (PE in z) using sensitivity maps obtained from the abdominal region of a healthy subject using a 32-channel torso coil (NeoCoil, Pewaukee, WI). Coronal phantom and in-vivo scans were performed with 10-fold acceleration on a 3T scanner (GE MR750, Waukesha, WI) using a 32-channel torso coil with FE in the superior-inferior direction. Conventional Cartesian acquisitions with the same variable-density poisson-disk sampling pattern and reconstruction method were performed for comparison in these studies.

Results

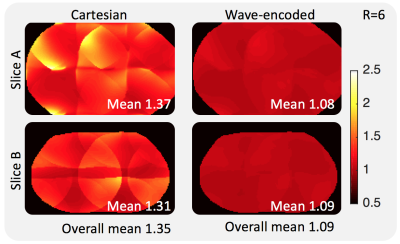
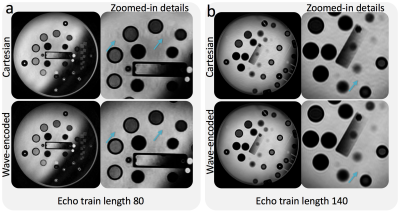
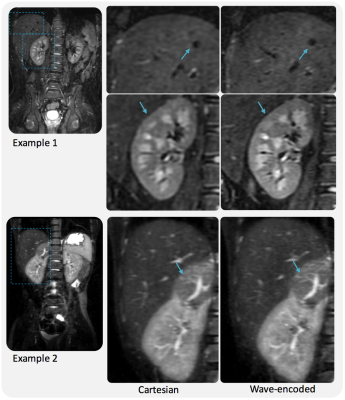
For a uniform undersampling factor of 6, wave encoding achieved a volumetric average g-factor of 1.09, while, for the same acceleration, the conventional Cartesian acquisition resulted in a g-factor of 1.35 (Fig. 3). Reconstructed phantom images show reduced aliasing/ghosting artifacts with the wave-encoded acquisition (Fig. 4). In-vivo images with wave encoding show less blurring and sharper structural details than conventional Cartesian acquisitions, as shown by arrows in Fig. 5.

Discussion

While sensitivity variations in the FE direction are usually not utilized for parallel imaging reconstruction of undersampled Cartesian acquisitions, wave encoding can use coil sensitivities more efficiently by creating voxel spreading in the FE direction2. Therefore, in clinical scans, reduced aliasing artifacts and less blurring can be achieved with wave encoding. The proposed self-calibrating gradient waveforms do not require additional prephasers and rephasers. Therefore, they fit well within the acquisition window, which helps to maintain clinically relevant scan parameters and T2 contrast. Auto-calibration of the wave-encoding PSF and the coil sensitivity maps using the under-sampled wave-encoded k-space reduces the complexity of integrating the proposed approach in clinical scans.

Conclusion

Compared to conventional Cartesian approaches with the same acceleration, the proposed variable-density wave-encoded 3D abdominal imaging technique achieves improved image quality with reduced aliasing and better structural delineation. It enables 10-fold acceleration for 3D FSE scans of the abdomen, allowing 3D FSE sequences to be less sensitive to subject motion.

Acknowledgements

GE Healthcare, NIH R01 EB009690, P41 EB015891.

References

1. Taviani V, Litwiller DV, Tamir JI, Loening AM, Hargreaves BA, and Vasanawala SS. Variable Density Compressed Sensing Single Shot Fast Spin Echo. Proc. Intl. Soc. Mag. Reson. Med. 2016; 24: 618.

2. Bilgic B, Gagoski BA, Cauley SF, Fan AP, Polimeni JR, Grant PE, Wald LL, Setsompop K. Wave-CAIPI for highly accelerated 3D imaging. Magnetic Resonance in Medicine. 2015; 73: 2152-2162.

3. Curtis A, et al. Wave-CS: Combining wave encoding and compressed sensing. Proc. Intl. Soc. Mag. Reson. Med. 2015; 23: 0082.

4. Cauley SF, Setsompop K, Bilgic B, Bhat H, Gagoski B, Wald LL. Autocalibrated wave‐CAIPI reconstruction; Joint optimization of k‐space trajectory and parallel imaging reconstruction. Magnetic Resonance in Medicine. 2016; Epub ahead of print.

5. Chen F, Taviani V, Tamir JI, Cheng JY, Zhang T, Song Q, Hargreaves BA, Pauly JM, Vasanawala SS. Self‐Calibrating Wave‐Encoded Variable‐Density Single‐Shot Fast Spin Echo Imaging. Journal of Magnetic Resonance Imaging. 2017 Sep 14. doi:10.1002/jmri.25853

6. Man LC, Pauly JM, Macovski A. Improved automatic off-resonance correction without a field map in spiral imaging. Magn Reson Med 1997;37:906–913.

7. Chen F, Zhang T, Cheng JY, Shi X, Pauly JM, Vasanawala SS. Autocalibrating motion‐corrected wave‐encoding for highly accelerated free‐breathing abdominal MRI. Magnetic resonance in medicine. 2017 Nov 1;78(5):1757-66.

8. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly J, Vasanawala SS, Lustig M. ESPIRiT - An Eigenvalue Approach to Autocalibrating Parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med 2014; 71:990-1001.

9. Cauley SF, Setsompop K, Bilgic B, Bhat H, Gagoski B, Wald LL. Autocalibrated wave‐CAIPI reconstruction; Joint optimization of k‐space trajectory and parallel imaging reconstruction. Magnetic Resonance in Medicine. 2016; Epub ahead of print.

10. Uecker M, Ong F, Tamir JI, Bahri D, Virtue P, Cheng JY, Zhang T, Lustig M. Berkeley Advanced Reconstruction Toolbox. Proc. Intl. Soc. Mag. Reson. Med. 2015; 23:2486.

Figures

Fig. 1 (a) Illustration of wave-encoding gradient waveforms for 3D FSE. For the waveform of the Gy gradient, the area of the first and last sinusoidal lobes was reduced by 50% to center the trajectory on the current phase-encoding (PE) line. (b) The variable density sampling pattern used for #PEy=256 and #PEz=192 at an effective reduction factor of 10, with a 24×32 fully sampled central region for coil sensitivity and wave-encoding PSF calibration.

Fig. 2 Pipeline of the proposed self-calibrating technique of 3D PSF. The 3D problem was split into 2D calibration problems. Two slices corresponding to y=0 and z=0 were extracted to perform 2D calibrations for the Gy and Gz waveforms, respectively (step 1&2). Each 2D calibration was performed by maximizing the square of the normalized image gradient3 (step 3&4). To improve calibration accuracy, 2D calibrations were performed iteratively, meaning previously calibrated 2D PSFs were used to as initialization of subsequent 2D calibrations. Finally, calibrated 2D PSFs were multiplied together to output the final 3D PSF (step 5).

Fig. 3 Comparison of g-factor maps between uniformly under-sampled Cartesian and wave-encoded scans at an acceleration factor of 6 with 160×100 phase-encodes. Wave encoding achieved an overall mean g-factor of 1.09, while Cartesian scans achieved a g-factor of 1.35.

Fig. 4 Comparison of reconstructed phantom images between variable-density under-sampled Cartesian and wave-encoded scans at (a) an echo train length of 80 and (b) an echo train length of 140. Arrows highlight artifacts and/or increased noise in the Cartesian acquisition that are reduced with the wave method.

Fig. 5 Clinical scans of a four-year-old patient (top) and an eight-year-old patient (bottom) at an acceleration factor of 10 with respiratory triggering. In example 1, the pyramids of the kidneys were sharper with wave encoding. In example 2, sharper blood vessels in a tumor of the right kidney can be observed with wave encoding. Scan parameters of example 1 for both Cartesian and wave-encoded scans were: TE=80ms, ETL=80, BW=±195Hz/pixel, acquisition matrix=320×226×172, and FOV=260mm×208mm×172mm. Scan parameters of example 2 were: TE=93ms, ETL=70, BW=±195Hz/pixel, acquisition matrix=320×226×192, and FOV=320mm×256mm×192mm. An over-sampling factor of 1.6 was used in FE direction in wave-encoded scans.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0211