Introduction

The implementation of ²³Na-sodium MRI in the clinical routine is of increasing interest since ²³Na MRI can provide valuable information on tissue viability^[1]. Since clinical scanners usually do not provide X-nuclei MRI additional hardware has to be used to enable both ²³Na and ¹H MRI. A design criterion of such double resonant RF setups is to keep the performance of the ¹H MRI approximately at the same level as single resonant setups while optimizing the ²³Na imaging. In order to increase the receiver sensitivity and enable parallel imaging for ¹H MRI multi-coil receiver arrays are the best choice. This work investigates the feasibility and performance of a double resonant 8 channel receive (Rx) head coil for ¹H and ²³Na MRI at 3T using EM simulations and a head model.

Methods

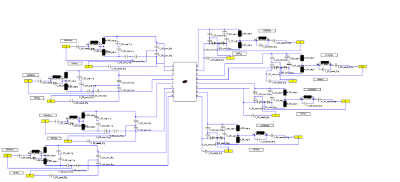
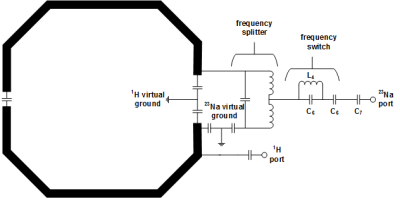
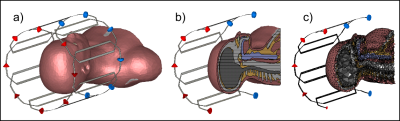
Three different head coils were designed for EM simulations (¹H reference coil, ²³Na reference coil, ²³Na/¹H double resonant coil). Each coil (diameter = 260 mm) was comprised of 8 loops (length = 260 mm, width = 134 mm, conductor width = 6 mm, cut twice for lumped elements and ports). The individual loops were decoupled iteratively via overlap. The matching and double resonant circuits were realized using a co-simulation (Figure 1). The double resonant loops were designed using the method introduced in reference^[2]. The electrical circuit for a single double resonant loop is plotted in Figure 2. The H-fields of the individual Rx channels were combined using the matched filter approach^[3]. All lumped elements were simulated including their equivalent series resistance in order to take the losses of the splitting network into account. A female head model was used as a phantom, which was generated from anatomical surface data using our FEM model processing pipeline^[4]. Figure 3 shows the EM simulation setup including the head model. EM fields were calculated using FEM simulations (CST–Computer Simulation Technology GmbH) with a tetrahedral mesh. Mesh refinement converged for all simulations to at least 2% for all S-parameters at the resonance frequencies 32.586 MHz (²³Na) and 123.2MHz (¹H).

Results

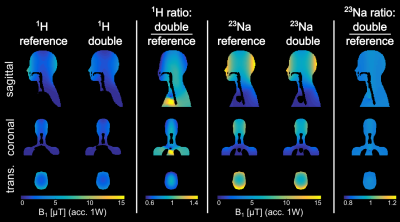
The simulated B₁-field (normalized to 1W accepted power) of the reference coils and the double resonant coil are plotted in Figure 4. For ¹H the losses of the double resonant coil compared to the reference coil vary from 6% in the center to 35% in the periphery of the head model evaluated in the central transversal plane. However, for ²³Na the losses of the double resonant coil differ from 9% in the center to 11% in the periphery evaluated in the same plane as above. The mean B₁-field in the center transversal plane drops 25% at the ¹H frequency and 11% at the ²³Na frequency for the double resonant coil, respectively.

Discussion

The double resonant coil showed no artifacts at the ¹H and the ²³Na frequency, which might have occurred due to the split circuits. The double resonant coil elements were optimized to be most sensitive at the ²³Na frequency. Due to this the ¹H sensitivity drops more close to the coils compared to the ²³Na sensitivity. This might occur due to the optimization for the ²³Na frequency as well as due to the overlap which was found to be slightly different for the two frequencies (the perfect overlap for the ²³Na frequency was selected). Despite all losses of the double resonant coil compared to the references the drop in B₁-sensitivity remained below 10% in the center of the head model.

Conclusion

The feasibility of a double resonant 8 channel Rx head coil was proven in simulation on a head model and the performance was compared to reference single tuned coils. Future work should focus on validating the findings in measurements as well as further optimization of the Rx coils, e.g. by splitting them more often.

Acknowledgements

No acknowledgement found.