0139
Ultimate intrinsic transmit efficiency for RF shimming1Center for Computational and Data-Intensive Science and Engineering (CDISE), Skolkovo Institute of Science and Technology, Moscow, Russian Federation, 2Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, New York University School of Medicine, New York, NY, United States, 3Bernard and Irene Schwartz Center for Biomedical Imaging (CBI), Department of Radiology, New York University School of Medicine, New York, NY, United States, 4Sackler Institute of Graduate Biomedical Sciences, New York University School of Medicine, New York, NY, United States
Synopsis
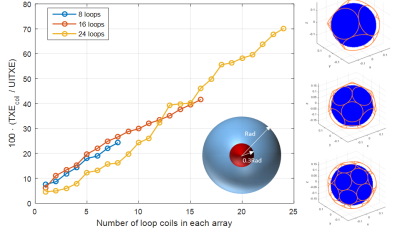
We introduce a new performance metric for RF shimming, the ultimate intrinsic transmit efficiency (UITXE), which provides an absolute reference independent of any particular coil design. We show in simulation that it represents a performance upper bound, which could be approached with finite transmit arrays with an increasing number of coils. In particular, we demonstrated that a 24-channel array could achieve 70% of the UITXE. UITXE could be employed in a straightforward manner in experiments to assess absolute performance of actual arrays and evaluate RF shimming approaches. The associated ideal current patterns could provide new insight for optimal array design.
Purpose
To introduce the ultimate intrinsic transmit efficiency (UITXE) as a performance upper bound for any RF shimming experiment, and propose it as a reference to assess the absolute performance of transmit (Tx) arrays.Theory and Methods
The transmit efficiency metric η, which was proposed for multiple channel transmission1,2, is defined as $$$η=\frac{\mathbf{w}^{H}\mathbf{\Gamma}\mathbf{w}}{\mathbf{w}^{H}\mathbf{\Phi}\mathbf{w}}$$$ where $$$\mathbf{w}$$$ is a complex-valued vector of RF shimming coefficients (amplitude and phase modulations) for each Tx channel. The matrix $$$\mathbf{\Gamma=\mathbf{C}^{H}\mathbf{C}}/M$$$ contains the B1+ squared per unit current for each Tx channel, averaged over the M voxels of the region of interest (ROI) for which Tx efficiency is being maximized. The matrix $$$\mathbf{\Phi}$$$ represents RF power dissipation over the volume (V) of the sample, and its elements are calculated as $$$\mathbf{\Phi}_{n,m}=\frac{1}{2}\intop_{V}\sigma(\mathbf{r})\mathbf{e}^{(n)}(\mathbf{r})^{*}\cdot\mathbf{e}^{(m)}(\mathbf{r})dV $$$ , where $$$\mathbf{e}^{(n)}$$$ is the electric field of the nth Tx channel per unit current. Note that the matrices $$$\mathbf{\Phi},\mathbf{\Gamma}$$$ are Hermitian by definition and $$$\mathbf{\Phi}$$$ is also a positive definite matrix, in the case of passive media. Hence the maximum Tx efficiency $$$\tilde{\mathbf{\eta}} $$$ is given by the largest eigenvalue of the associated generalized eigenvalue problem $$$\mathbf{\Gamma w}=\lambda\mathbf{\Phi w} $$$. The corresponding eigenvector $$$\tilde{\mathbf{w}} $$$ contains the optimal RF shimming coefficients that achieve maximum efficiency. In this work, we constructed a complete basis of electromagnetic fields using vector spherical harmonic modes (4232 in total), generated by electric currents flowing on a spherical shell (18cm radius), enclosing a homogeneous sphere (15cm radius) with average brain electrical properties3. Since the operator that maps currents to fields is compact, $$$\tilde{\mathbf{\eta}} $$$ converges to the UITXE as the number of modes increases. We investigated UITXE as a function of main magnetic field strength (B0) and for different target ROIs. We assessed maximum Tx efficiency with respect to UITXE for various arrays of loop coils at 7T. Coils’ electromagnetic fields were calculated with a volume integral equation solver4 using piecewise linear basis functions.Results
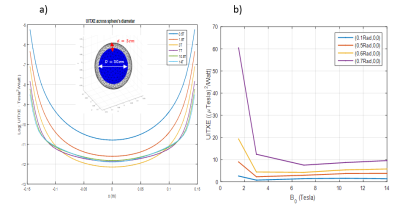
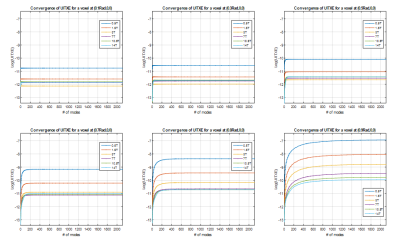
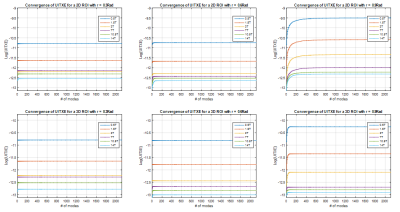
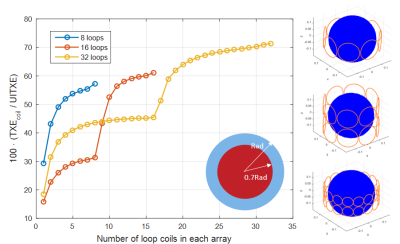
Fig. 1a shows UITXE for single voxels across the sphere’s diameter for different B0 values, whereas Fig. 1b shows UITXE at particular voxel locations for increasing B0. As for the UISNR5,6, UITXE increases as the target voxel approaches the surface of the sphere. Interestingly, UITXE decreases with B0 up to 3T and then starts to slowly increase for higher B0 values. Fig. 2 shows convergence of the UITXE calculations vs. number of modes for different voxel positions and B0. The closer the voxel is to the sphere surface, the more modes are required for convergence. Fig. 3 illustrates the convergence of UITXE when maximizing Tx efficiency in 2D and 3D ROIs of different sizes, rather than at single voxels. UITXE required more modes to converge for 2D than 3D ROIs. Figs. 4 and 5 show the maximum Tx efficiency achievable at 7T with finite arrays as a percentage of the UITXE, for a 3D and a 2D ROI, respectively. In both cases, UITXE was approached more closely by increasing the number of loops. For the 3D ROI (an inner sphere with radius equal to 30% the object radius), enclosing Tx arrays with 8, 16, and 24 loops yielded 24%, 41%, and 70% of the UITXE, respectively. For the 2D ROI (a circle covering 70% the central transverse section), belt shaped Tx arrays with 8, 16, and 32 loops yielded 57%, 61%, and 71% of the UITXE, respectively.Discussion and Conclusions
UITXE represents a theoretical upper bound for coil performance, since it depends only on the size and electrical properties of the sample and on the target ROI, but it’s independent of any particular coil design. Although the optimization algorithm does not enforce any particular flip angle distribution, as in the case of UISAR3, one can expect that maximizing Tx efficiency would naturally prevent B1+ nulls within the target ROI2. UITXE could be used as an absolute reference to assess Tx arrays and RF shimming techniques, since η is independent of any scale factor in the shimming weights (therefore independent of any overall change in transmit voltage) and, furthermore, can be practically evaluated in experiments2. Ongoing future work includes studying UITXE for a realistic human head and combining the current modes using the corresponding optimal shimming coefficients $$$ \tilde{\mathbf{w}} $$$ to derive ideal current patterns7 resulting in UITXE, which could provide physical insight and a concrete design target to RF engineers. We also plan to evaluate absolute performance of actual Tx arrays with respect to UITEX in phantom experiments.Acknowledgements
This work was supported in part by NIH R01 EB024536 and was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).References
[1] Zhu Y, Deniz CM, Alon L, Fautz HP, Sodickson DK. Undestanding parallel transmit array efficiency. In Proceedings of the 18th Annual Meeting of ISMRM, Stockholm, Sweden, 2010. p. 1518.
[2] Deniz CM, Brown R, Lattanzi R, Alon L, Sodickson DK, Zhu Y. Maximum efficiency radiofrequency shimming: theory and initial application for hip imaging at 7 Tesla. Magn Reson Med 2013;69(5):1379-1388.
[3] Lattanzi R, Sodickson DK, Grant AK, Zhu Y. Electrodynamic constraints on homogeneity and radiofrequency power deposition in multiple coil excitations. Magn Reson Med. 2009;61(2):315-34.
[4] A.G. Polimeridis, J.F. Villena, L. Daniel, J.K. White. Stable FFT-JVIE solvers for fast analysis of highly inhomogeneous dielectric objects, Journal of Computational Physics, Vol 269, July 2014, p. 280-296.
[5] Wiesinger F, Boesiger P, Pruessmann KP. Electrodynamics and ultimate SNR in parallel MR imaging. Magn Reson Med 2004;52:376–390.
[6] Guerin B, Villena JF, Polimeridis AG, Adalsteinsson E, Daniel L, White JK, Wald LL. The Ultimate Signal-to-Noise Ratio in Realistic Body Models. Magn Reson Med 2017, 78: 1969–1980.
[7] Lattanzi R, Sodickson DK. Ideal current patterns yielding optimal signal-to-noise ratio and specific absorption rate in magnetic resonance imaging: computational methods and physical insights. Magn Reson Med 2012;68(1):286-304.
Figures