0138

Optimization and validation of dipole antenna geometry for body imaging at 10.5T

Bart R. Steensma¹, Pierre-Francois van de Moortele², Arcan M. Erturk², Andrea Grant², Gregor Adriany², Gregory J. Metzger², and Alexander J.E. Raaijmakers^1,3

¹Radiology, University Medical Center Utrecht, Utrecht, Netherlands, ²Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, ³Biomedical Image Analysis, Eindhoven University of Technology, Eindhoven, Netherlands

Synopsis

Body MRI at 10.5T shows potential for improving signal-to-noise ratio compared to 7T, but is limited by increased specific absorption rate (SAR) levels. In this work, the geometry of a dipole antenna is optimized for body imaging with low SAR levels at 10.5T. The optimized dipole geometry is compared to a previous design in simulations on a human model, where it is shown that SAR levels can be decreased by 36% for an equal transmit efficiency. Simulations are validated by magnetic resonance thermometry and B₁⁺-mapping experiments with a 12-channel multi-transmit array.

Purpose

For body MRI at ultra-high field (UHF, B₀≥7T), the use of radiative dipole antennas as surface array elements in a multi-transmit setup is becoming increasingly common^1-7. A transmit array consisting of fractionated dipole antennas has been presented before for body imaging at 10.5T⁶. With this array, it was demonstrated that compared to 7T, signal-to-noise-ratio can potentially be improved by over a factor 2 for human prostate imaging. However, peak local Specific Absorption Rate (SAR) also increases within a comparable range. The transmit performance and local peak SAR of a dipole antenna depends strongly on its geometry^1,2,8-10. In this work, the effect of using a sinusoidal dipole shape rather than a straight or fractionated dipole is investigated. The aim of this work is to optimize the sinusoidal geometry of the dipole for body imaging at 10.5T, and to select the antenna geometry that has the lowest peak SAR for a given transmit efficiency.

Methods

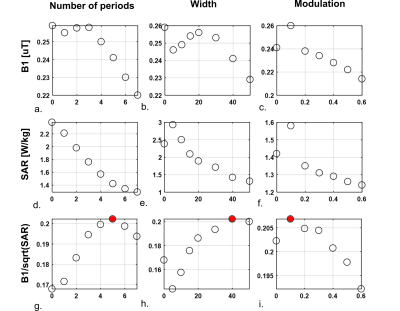
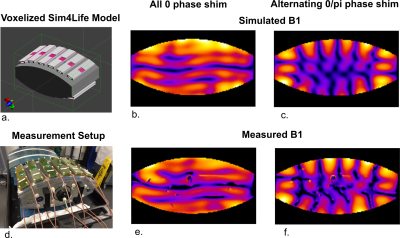
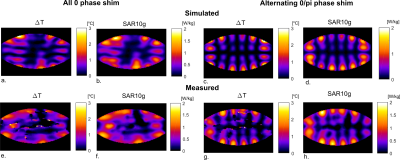
Finite difference time-domain simulations (Sim4Life, Zurich Medtech, Zurich, Switzerland) were used to model two sinusoidal shaped dipole antennas on a phantom with tissue-like properties (σ = 0.37 S/m ε_r= 34). The geometry of the dipole antennas was varied by changing the number of periods, the width and the modulation of the sinusoidal geometry (figure 1). The length of the dipole antennas was kept equal to the length of the fractionated dipole antenna for 10.5T in all cases^1,6. Phase shimming was applied on a cubic region of interest (ROI, 10 cm³) located at a depth of 10 cm in the phantom. The different antenna geometries were evaluated by calculating the 10g-averaged peak SAR, and by assessing B₁⁺ in the ROI. The optimum antenna was selected based on the highest B₁⁺/√SAR_10g in the ROI. The new antenna design was compared to a previous design by simulating two 12-channel setups on the torso of Duke¹¹: a setup consisting of fractionated dipole antennas and a setup consisting of the optimized antenna (snake antenna). For validation of the simulations, B₁⁺-maps (actual flip angle method, TR 20/120 ms¹²) and Magnetic Resonance Thermometry maps (MRT, Proton-Resonance Frequency-shift method¹³) were acquired experimentally on the Siemens Magnetom 10.5T system, and compared to numerical simulations. MRT was done on a Hydroxyethyl Cellulose (HEC) phantom, containing 2.97 g NaCl/L and 14 g HEC/L. RF heating for the MRT experiments was performed using a protocol with the following relevant scan parameters: input voltage 120 V, TR 7.5 ms, pulse length 0.5 ms, sinc bandwidth product = 1, total heating time 4:00 minutes, flip angle 180^o, duty cycle 6.67%.

Results

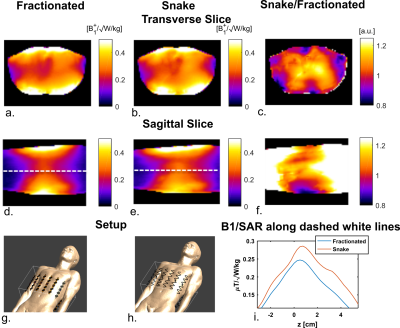
Figure 2 shows the effect of antenna geometry on antenna performance. Increasing the number of periods, the width or the modulation decreases SAR but also decreases B₁⁺.However, transmit efficiency does not decrease at the same rate as SAR, resulting in certain optimal parameters to exist. Based on these simulation results, an antenna geometry with 5 periods, a meander width of 40 mm and a modulation of 0.1 was chosen as the optimum geometry. This antenna design is referred to as the snake antenna. Figure 3 shows field distributions in a transverse slice through the torso for a setup of 12 fractionated dipoles and snake antennas. The field distributions shown here represent the optimum B₁⁺ in every voxel, normalized to the maximum SAR_10gfor a phase-only shim solution. In the central region of the slice, B₁⁺/√SAR_10g increases up to 25% when using the snake antenna array. Figure 4 shows a comparison of simulated and measured B₁⁺-maps in a phantom for two different phase settings (all phases 0, or alternating 0/pi phase offset per channel). Simulation results were normalized per channel based on the ratio between simulated and measured single-channel B₁⁺-maps. Figure 5 shows simulated and measured temperature and SAR maps that were obtained using the same power normalization and phase offsets.The field patterns and the scale of the simulations are in good correspondence for both the B₁⁺-maps as the MRT results.

Discussion

It was demonstrated in simulations that by optimizing the dipole geometry, the B₁⁺/√SAR_10g level can be increased up to 25%. This implies that for an equal B₁⁺, SAR levels are 36% lower, making it potentially possible to decrease the scan time by the same amount. Simulations results were validated by means of B₁⁺-maps and MR Thermometry and are in good correspondence. The comparison of simulation and experimental results will be submitted to the US Food and Drug Administration for approval of scans on human volunteers.

Conclusion

By adapting the geometry of a dipole antenna it was possible to decrease effective peak local SAR levels by 36%. Simulation results were validated experimentally by B₁⁺-maps and MR Thermometry.

Acknowledgements

S10 Grant RR029672 “Console for 10.5 Tesla Whole Body MRI System”

BTRC Grant P41 EB015894

Dutch Technology Foundation STW Grant 13783

References

1. Raaijmakers AJE, Ipek O, Klomp DWJ, Possanzini C, Harvey PR, Lagendijk JJW, den Berg CAT. Design of a radiative surface coil array element at 7 T: The single-side adapted dipole antenna. Magn Reson Med. 2011; 66:1488–1497.

2. Wiggins GC, Zhang B, Lattanzi R, Chen G, Sodickson DK. The Electric Dipole Array: An Attempt to Match the Ideal Current Pattern for Central SNR at 7 Tesla. Proc. Intl. Soc. Mag. Reson. Melbourne. 2011; 541.

3. Winter L, Özerdem C, Hoffmann W, Santoro D, Müller A, Waiczies H, Seemann R, Graessl A, Wust P, Niendorf T. Design and Evaluation of a Hybrid Radiofrequency Applicator for Magnetic Resonance Imaging and RF Induced Hyperthermia: Electromagnetic Field Simulations up to 14.0 Tesla and Proof-of-Concept at 7.0 Tesla. PLoS One. 2013; doi: 10.1371/journal.pone.0061661.

4. Raaijmakers AJE, Italiaander M, Voogt IJ, Luijten PR, Hoogduin JM, Klomp DWJ, van den Berg CAT. The fractionated dipole antenna: A new antenna for body imaging at 7 Tesla. Magn Reson Med. 2016; 75:1366–1374.

5. Oezerdem C, Winter L, Graessl A, Paul K, Els A, Weinberger O, Rieger J, Kuehne A, Dieringer M, Hezel F, Voit D, Frahm J, Niendorf T. 16-channel bow tie antenna transceiver array for cardiac MR at 7.0 tesla. Magn Reson Med. 2016; 75:2553–2565.

6. Ertürk MA, Wu X, Eryaman Y, Van de Moortele P-F, Auerbach EJ, Lagore RL, DelaBarre L, Vaughan JT, Uğurbil K, Adriany G, Metzger GJ. Toward imaging the body at 10.5 tesla. Magn Reson Med. 2016; 77:434–443.

7. Ertürk MA, Raaijmakers AJE, Adriany G, Ugurbil K, Metzger GJ. A 16-channel combined loop-dipole transceiver array for 7 Tesla body MRI. Magn Reson Med. 2016; 77:884–894.

8. Wiggins GC, Lakshmanan K, Chen G (2015) The Distributed Inductance Electric Dipole Antenna. Proc. Intl. Soc. Mag. Reson. Vancouver. 2015; 23:3100.

9. Steensma BR, Obando AV, Klomp DWJ, van den Berg CAT, Raaijmakers AJE. Body imaging at 7 tesla with much lower SAR levels: an introduction of the Snake Antenna Array. Proc. Intl. Soc. Mag. Reson. Singapore. 2016; 0395

10. Connell IRO, Menon RS. Shape-Optimization of Electric Dipoles for Human Head Imaging at 7 Tesla. Proc. Intl. Soc. Mag. Reson. Med. 2017; 1130.

11. Kuster AC and WK and EGH and KH and MZ and EN and WR and RJ and WB and JC and BK and PS and H-PH and J. The Virtual Family—development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol. 2011; 55:N23.

12. Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn Reson Med. 2007; 57:192–200.

13. Rieke V, Butts, K. MR Thermometry. J magn Reson Imaging. 2008; 27(2): 376-390.

Figures

Figure 1: 1a. Optimization setup: 2 antennas on a phantom with human tissue-like properties, ε=34, σ = 0.4 S/m. 1b. Optimization parameters for the sinusoidal antenna geometry. The parameters were optimized sequentially as indicated by the red arrows.

Figure 2: Optimization results versus optimization parameters. 2a-c. B₁ ⁺ in the ROI for the different parameters. 2d-f. maximum SAR_10g in the phantom. 2g-i. B₁⁺ normalized to maximum SAR_10g. The parameters of the optimal antenna design are marked in red.

Figure 3: Simulation results on Duke. Optimum B₁⁺ in every voxel, normalized to the maximum local peak SAR_10g, considering equal and uniform power input. 3a-c. Results in the central transverse slice. 3d-f. Results in a central sagittal slice. 3g-h. Simulation setup for both antenna arrays. 3i. Comparison of the two arrays along a line through sagittal slice.

Figure 4: simulated and measured B₁⁺-maps on a HEC phantom. 4a-c. Simulation setup and results for two different shim settings. 4d-f. Measurement setup and results for the same shim settings. The simulated model was based on a Computed Tomography scan of the measurement setup.

Figure 5: Simulated and measured temperature maps and derived SAR_10g-maps. 3a-d. Simulated results. 3e-h. Measured results. Results are either ΔT or SAR_10g, for an all 0 or alternating 0/pi phase shim, as indicated by the annotations.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)

0138