0079
Partial velocity-compensated diffusion encoding for combined motion compensation and residual vessel signal suppression in liver DWI1Department of Diagnostic and Interventional Radiology, Technical University of Munich, Munich, Germany, 2Philips Japan, Tokyo, Japan, 3Philips MR Clinical Science, Best, Netherlands, 4Philips Healthcare, Hamburg, Germany
Synopsis
Despite its strong clinical significance in lesion detection and tumor staging, liver DWI remains challenged by its strong sensitivity to motion effects. Motion-compensated diffusion encoding schemes have been recently proposed to improve DW liver signal homogeneity especially in the left liver lobe, a region typically affected by cardiac motion. However, motion-compensated diffusion encoding is associated with hyperintense vessel signal even at high b-values, which can obscure lesion detection. The present work proposes a partial velocity-compensated diffusion encoding for combined motion compensation and residual vessel signal suppression in liver DWI.
Purpose
Diffusion-weighted imaging (DWI) is a valuable tool for the detection and characterization of liver lesions [1,2]. For high quality, reproducible DW images of the liver, one of the biggest challenges is the combination of cardiac, respiratory, and subject involuntary motion. Despite the employment of single-shot techniques, the motion of cardiac activity and respiration exercised on the deformable liver leads to intravoxel dephasing and hence, signal loss. Previous methods for improving insensitivity to motion in liver DWI primarily involved breath-holding or respiratory triggering for respiratory motion, and cardiac gating or motion-compensated diffusion encoding (mcDE) for cardiac motion [3-8]. For patient comfort and higher scan efficiency, a combination of respiratory triggering and mcDE is typically preferred. However, when mcDE is used in the presence of vessels with predominantly flow (coherent) motion, some vessels remain hyperintense even at high b-value. Such regions with residual hyperintense vessel signal can obscure lesion detection and therefore need accounting for. The current work proposes a method of diffusion encoding in liver DWI that enables both reduced sensitivity to motion and increased vessel signal suppression.Methods
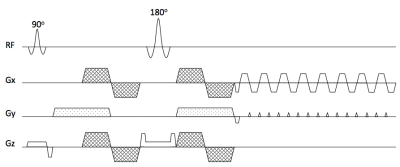
Partial velocity-compensated diffusion encoding scheme (vmcpgse)
The proposed diffusion encoding combines velocity-compensated diffusion encoding (vmc) on two axes and traditional Stejskal-Tanner diffusion encoding (pgse) on the third axis. The pgse waveform suppresses vessel signal and the proposed diffusion encoding scheme selects the pgse axis aiming to reduce sensitivity to motion based on the following two arguments.
1) The pgse waveform is applied along the direction that is least affected by cardiac motion, which has been shown by Kwee et al to be the A-P direction [4].
2) Partial Fourier encoding (PF) needs to be used to shorten the echo time. However, with PF, motion-induced k-space shifts can drive the k-space center outside of the acquired region, leaving unusable noisy data [9]. In the case of rigid body motion, the direction of k-space shift is the cross product between the axis of the rotation and the diffusion encoding direction [10, 11] and the k-space shift along the phase encoding direction (ky, or partial Fourier direction) is$${\Delta}k_y=\gamma\int{[G_z(t)\theta_x(t) - G_x(t)\theta_z(t)]dt} \ (1)$$
where $$$G_x, G_z$$$ are the diffusion encoding gradients along the x and the z direction, respectively and $$$\theta_x, \theta_z$$$ are the rotation angles around the x and the z axis, respectively. Equation (1) implies that the shift along the ky direction is independent of the diffusion encoding gradient Gy. Therefore, when PF is used, the pgse waveform should be applied along the phase encoding direction to minimize the probability of missing the k-space center.
Based on the above arguments the pgse waveform in the vmcgse scheme should be applied on the phase encoding axis. The proposed diffusion encoding scheme (vmcpgse-p) is thus depicted in Figure 1.
MR measurement
In-vivo experiments were carried out in 3 subjects to assess the performance of the proposed vmcpgse-p diffusion encoding scheme in motion resistance and vessel signal suppression. To show the benefits in terms of k-space shifts when the pgse waveform is applied along the phase encoding direction, acquisitions with three varieties of vmcpgse in which the pgse waveform is applied along the frequency (vmcpgse-m), phase (vmcpgse-p), and slice encoding (vmcpgse-s) directions were performed. For comparison, experiments with pgse in all three axes and vmc in all three axes were also performed. Imaging parameters included: acquisition voxel size = 3x3x6mm3, 6 slices in the upper part of the liver, 3 diffusion encoding directions ([-0.5 -1 -1], [1 0.5 -1], [1 -1 0.5]), b-value of 600s/mm2, 10 averages, TE=61/67ms for pgse/vmc and vmcpgse, full Fourier encoding for pgse and PF factor of 0.6 for vmc and vmcpgse. All experiments were performed on a 3T Ingenia system (Philips, Best, the Netherlands) using anterior and posterior torso coils for receiving.
Results
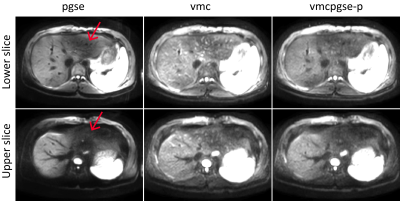
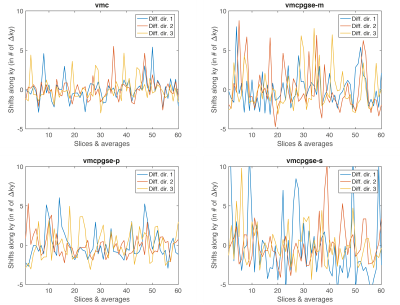
Figure 2 shows that vmc increases DW liver signal homogeneity in the left liver lobe but suffers from increased vessel signal throughout the liver. The proposed diffusion-encoding vmcpgse-p maintains the left liver lobe signal in the high b-value images while providing good overall signal suppression (Fig. 2). Figure 3 shows a decreased k-space phase encoding shift in the vmcpgse-p compared to vmcpgse-m and vmcpgse-s diffusion encoding. The lowest standard deviation of k-space shift across directions and slices is achieved in all subjects using vmc (Fig. 4). However, the standard deviation of k-space shift is also lower in vmcpgse-p compared to vmcpgse-m and vmcpgse-s diffusion encoding in all three subjects (Fig. 4).Conclusion
The proposed partial velocity-compensated diffusion encoding combining velocity compensation in the frequency and slice encoding axes and traditional Stejskal-Tanner diffusion in the phase encoding axis enables reduced motion sensitivity in liver DWI while maintaining good vessel signal suppression.Acknowledgements
The present work was supported by Philips Healthcare.References
[1] Namimoto T, Yamashita Y, Sumi S, et al. Focal liver masses: characterization with diffusion-weighted echo-planar MR imaging. Radiology 1997; 204:739-744.
[2 ] Ichikawa T, Haradome H, Hachiya J, et al. Diffusion-weighted MR imaging with a single-shot echoplanar sequence: detection and characterization of focal hepatic lesions. Am J Roentgenol 1998; 170:397-402.
[3] Taouli B, Sandberg A, Stemmer A, et al. Diffusion-weighted imaging of the liver: comparison of navigator triggered and breathhold acquisitions. J Magn Reson Imaging 2009; 30:561-568.
[4] Kwee TC, Takahara T, Niwa T, et al. Influence of cardiac motion on diffusion-weighted magnetic resonance imaging of the liver. Magn Reson Mater Phy 2009; 22:319-325.
[5] Nasu K, Kuroki Y, Minami M. Feasibility of diffusion-weighted imaging under split breath-hold acquisition and postprocessing (DWI-SBAP): an attempt to suppress hepatic pseudo-anisotropy. Jpn J Radiol 2009; 27:78-850.
[6] Ozaki M, Inoue Y, Miyati T, et al. Motion artifact reduction of diffusion-weighted MRI of the liver: use of velocity-compensated diffusion gradients combined with tetrahedral gradients. J Magn Reson Imaging 2013; 37:172-178.
[7] Metens T, Absil J, Denolin V, et al. Liver apparent diffusion coefficient repeatability with individually predetermined optimal cardiac timing and artifact elimination by signal filtering. J Magn Reson Imaging 2016; 43:1100-1110.
[8] Aliotta E, Wu HH, Ennis DB. Convex optimized diffusion encoding (CODE) gradient waveforms for minimum echo time and bulk motion-compensated diffusion-weighted MRI. Magn Reson Med 2017; 77:717-729.
[9] Storey P, Frigo FJ, Hinks RS, Mock BJ, Collick BD, Baker N, Marmurek J, Graham SJ, Partial k-Space reconstruction in single-shot diffusion- weighted echo-planar imaging. Magn Reson Med 2007, 57:614-619.
[10] Anderson AW, Gore JC, Analysis and correction of motion artifacts in diffusion-weighted imaging. Magn Reson Med 1994; 32:379-387.
[11] Van AT, Karampinos DC, Georgiadis JG, Sutton BP, k-space and image-space combination for motion-induced phase-error correction in self-navigated multicoil multishot DWI. IEEE TMI 2009; 28:1770-1780.
Figures