0071

Learning a Variational Network for Reconstruction of Accelerated MRI Data
Kerstin Hammernik1, Erich Kobler1, Teresa Klatzer1, and Michael P Recht2

1Institute of Computer Graphics and Vision, Graz University of Technology, Graz, Austria, 2Center for Biomedical Imaging and Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, NYU School of Medicine, New York, NY, United States

Synopsis

In this work, we propose variational networks for fast and high-quality reconstruction of accelerated multi-coil MR data. A wide range of experiments and a dedicated user study on clinical patient data show that the proposed variational network reconstructions outperform traditional reconstruction approaches in terms of image quality and residual artifacts. Additionally, variational networks offer high reconstruction speed, which is substantial for the incorporation into clinical workflow.

Introduction

Traditional handcrafted iterative reconstruction approaches rely on the three Compressed Sensing (CS)1-3 conditions: (1) sparsity in a transform domain, (2) incoherence of undersampling artifacts, and (3) a non-linear reconstruction algorithm. Furthermore, traditional approaches treat every exam as a new individual optimization problem. Deep learning4,5 provides a way to shift this optimization to an offline training task, enabling knowledge extraction about the expected structure of artifacts and appearance of the anatomy, which is then used to reconstruct new unseen data. Inspired by variational models and deep learning, we introduce variational networks (VNs)6 for reconstruction of clinical accelerated multi-coil MR data, allowing us to include prior knowledge of artifacts and to overcome the requirements for CS.

Methods: Variational Networks

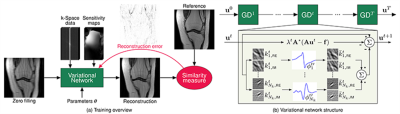
We embed a generalized CS reconstruction, formulated as a variational model, in a gradient descent scheme consisting of a fixed number of steps (see Figure 1). During an offline training procedure, the output of the VN is compared to an artifact-free reference reconstruction, in order to get a new estimate of the model parameters such as filter kernels, activation functions and data term weights. After the time consuming training, the trained model can be applied efficiently to previously unseen data. The design of the VN was kept consistent for all our experiments. We fixed the number of steps to 10, in each step 24 complex-valued 11x11 filters and their corresponding activation functions, i.e., non-linearities, were learned together with the data term weight, resulting in a total of 131,050 network parameters. For training, we used the mean-squared error on magnitude images as similarity measure.

Data Acquisition

To include versatile data in terms of anatomy, pathology, gender, age, and body mass index, we scanned 20 patients undergoing clinical knee examinations on a 3T Siemens Magnetom Skyra using a 15-channel knee coil (IRB-approved). The clinical knee protocol consisted of 5 fully-sampled 2D turbo spin echo sequences, differing in terms of signal-to-noise ratio (SNR), contrast, orientation and matrix size. The dataset was split into 10 patients for training and 10 patients for testing. Prospectively undersampled data were additionally acquired for one patient.

Experiments

We trained and evaluated our VN approach for acceleration factors R=3 and R=4 and investigated both regular Cartesian and variable-density random7 undersampling patterns applied in a retrospective way. The VN reconstructions were compared to linear CG SENSE8, CS non-linear Total Generalized Variation (TGV)9,10 and dictionary learning reconstructions both qualitatively and quantitatively in terms of normalized root mean squared error (NRMSE) and structural similarity index (SSIM)11. Finally, we applied the trained networks to prospectively accelerated data.

Results

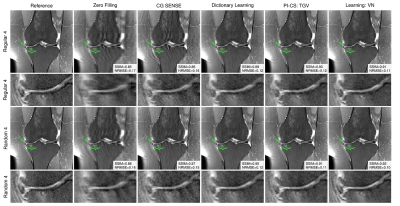
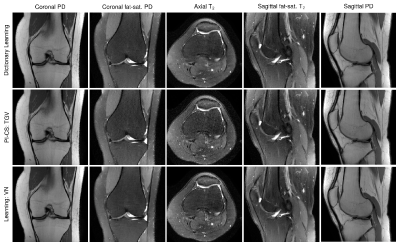
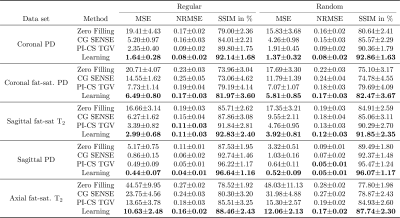
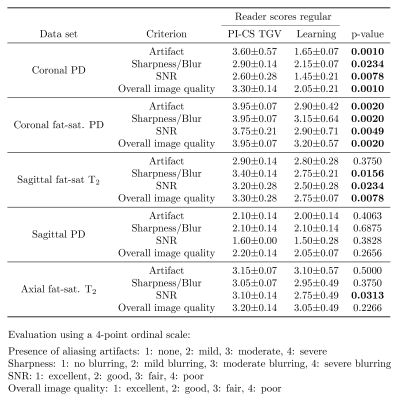
Qualitative results for low-SNR coronal fat-saturated proton-density scans are shown in Figure 2 for R=4, along with the quantitative evaluation for the depicted slice. Results for prospectively undersampled data with the same acceleration factor are illustrated in Figure 3. These results show that the VN reconstructions appear sharper and show reduced artifacts compared to the other methods. In Table 1, the qualitative observations are supported by the quantitative evaluation (R=4). Table 2 indicates that the image quality is significantly better for both coronal scans and sagittal T2 weighted scans. The difference in image quality for the axial scan and sagittal proton-density weighted scan is not significant (α=0.05) .

Discussion and Conclusion

In this work, we proposed VNs that enable high-quality, artifact-free reconstructions, while preserving important features and pathologies for a wide range of clinical patient data compared to traditional reconstruction approaches. Once all model parameters are learned in an offline training step, the reconstruction time of new data is fast, i.e., 193 ms on a single graphics card. Therefore, VNs offer easy integration into clinical workflow.

Acknowledgements

We acknowledge grant support from the Austrian Science Fund (FWF) under the START project BIVISION, No. Y729, ERC starting grant ”HOMOVIS”, No. 640156., NIH P41 EB017183, NIH R01 EB000447 and NVIDIA corporation.

References

[1] Candes EJ, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory 2006;52:489–509.

[2] Donoho DL. Compressed sensing. IEEE Trans Inf Theory 2006;52:1289–1306.

[3] Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182–1195.

[4] LeCun Y, Bengio Y, Hinton G. Deep learning. Nature 2015;521:436–444.

[5] Goodfellow I, Bengio Y, Courville A. Deep learning. Cambridge, MA:MIT Press; 2016.

[6] Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a Variational Network for Reconstruction of Accelerated MRI Data”. Magn Reson Med 2018;79:3055-3071.

[7] Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182–1195

[8] Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42:952–962.

[9] Knoll F, Bredies K, Pock T, Stollberger R. Second order total generalized variation (TGV) for MRI. Magn Reson Med 2011;65:480-491.

[10] Bredies K, Kunisch K, Pock T. Total generalized variation. SIAM JImaging Sci 2010;3:492–526.

[11] Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans ImageProcess 2004;13:600–612.

Figures

Figure 1: (a) Raw k-space data, coil-sensitivity maps are fed along with the zero filling solution to the variational network (VN). During training, the reconstruction is compared to a reference using some similarity measure. The reconstruction error is then used to update the parameters during training. The VN itself consists of T gradient descent steps. (b) depicts a single gradient descent step, where the gradient corresponds to the gradient of the generalized compressed sensing model. Filter kernels for real and imaginary part are learned together with their corresponding activation function and the data term weights.

Figure 2: Reconstruction results of a coronal fat-saturated proton-density-weighted scan with acceleration R=4, for both regular and random sampling. The scans of the 57-year-old female patient show broad-based, full-thickness chondral loss and a subchondral cystic change, indicated by the green bracket, and an extruded and torn medial meniscus, indicated by the green arrow. The VN reconstruction has less residual artifacts and appears sharper than the other reconstruction methods. The results for regular sampling are blurrier than for random sampling. The observations are supported by the quantitative values.

Figure 3: Prospectively undersampled data of a 27-year-old female volunteer. We observe good reconstruction quality for proton-density scans. The TGV reconstructions of fat-saturated scans show a blocky, artificial appearance, while we observe a noise pattern for dictionary learning results. VN reconstructions have the least amount of remaining artifacts and most improved SNR.

Table 1: Quantitative evaluation (MSE, NRMSE, SSIM) for regular and random sampling and acceleration factor R=4. These results support the qualitative observations. The learning-based VN reconstructions outperform the reference methods in all cases. Random sampling performs better than regular sampling for this acceleration factor.

Table 2: Evaluation of the reader study, comparing TGV and VN reconstructions (R=4). We report mean and standard deviation, averaged over the two readers along with the p-value resulting from the one-sided Wilcoxon signed-rank test. For a significance level α=0.05, the null hypothesis that TGV reconstruction are better or equal VN reconstructions is rejected for most of the quality measures and sequences.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0071