Introduction

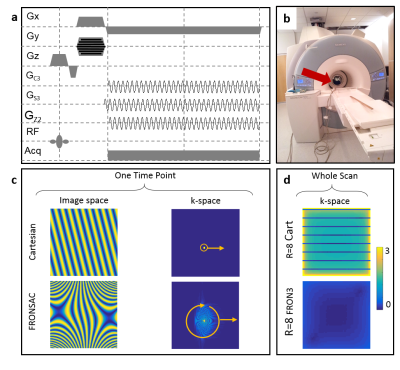
In this work we demonstrate in vivo and in vitro that the application of sinusoidal NLGs improve undersampled Cartesian encoding (Figure 1a). Linear gradients sample k-space one point at a time, and receiver arrays sample a static distribution of k-space. In contrast, NLGs dynamically vary the size and shape of the sampling functions in k-space (Figure 1c), which provides more degrees of freedom to design an efficient trajectory to measure k-space. The encoding efficiency is increased when an undersampled linear acquisition is enhanced with FRONSAC encoding as measured with a previously introduced k-space metric (Figure 1d) (1). Previous work showed that FRONSAC reduces undersampling artifacts in accelerated imaging for a variety of linear gradient sequences (2). In the current work presented here, we show the first experimental Cartesian FRONSAC results, confirming the theoretical reduction of under sampling artifacts and we investigate features of FRONSAC critical to clinical imaging. In addition to providing experimental confirmation of the reduced undersampling artifact, we demonstrate that FRONSAC yields more benefit from the new generation reconstruction algorithms, now becoming commercially available (3-5). We also show that Cartesian FRONSAC yields benign artifacts in the presence of experimental imperfections or when the gradient fields deviate from the perfect spherical harmonics used in the original paper, thereby providing robust performance in a clinical setting. A single FRONSAC gradient is also shown to enhance undersampled image quality for nearly any imaging prescription, despite changes in the linear gradients associated with different image dimensions, slice orientation or spatial resolution. As such, the method does not require extensive field mapping. It is applicable to a number of different sequence types and is demonstrated here using both gradient echo and fast spin echo sequences.

Methods

In vivo and phantom experiments on a 3T MRI scanner (MAGNETOM Trio Tim, Siemens Healthcare, Erlangen, Germany) with an 8 channel RF head coil (Siemens) were performed at Yale University using a NLG insert (Tesla Engineering Ltd, Storrington, UK) (Figure 1b) that generates 3 spherical harmonic gradient fields: G_C3 (X³-3XY²), G_S3 (3YX²-Y³), and G_Z2 (X²+Y²) with maximum strengths of 3254.8 mT/m³, 3155.4 mT/m³ and 475.08 mT/m². Phantom experiments performed at the University Medical Center Freiburg used an 84 channel matrix gradient coil (6). A non-optimized cluster of elements approximated a C3 field with maximum strength of 452 mT/m³. Transverse slices at isocenter with a FOV of 250 mm were acquired with 1024 readouts with 128 excitations. GRE imaging parameters at Yale University were: TR=1000 ms/TR=600 ms; TE=18 ms; bandwidth=50 Hz/pixel; flip angle=30°/15°; slice thickness=3 mm, maximum C3/S3/Z3 strength=325.3 mT/m³, 316.7 mT/m³ and 41.6 mT/m² with oscillation frequency of ω₀/2pi=3.2 kHz. TSE imaging at Yale University parameters were: TR=3000 ms; turbo factor=8; echo spacing=24 ms; bandwidth=100 Hz/pixel; slice thickness=5 mm, maximum C3/S3/Z2 strength=390.7 mT/m³, 380.1 mT/m³ and 50.0 mT/m² with oscillation frequency of ω₀/2pi=4.8 kHz. University of Freiburg Medical Center parameters were: TR=700 ms; TE=11.2 ms; bandwidth=78.125 Hz/pixel; flip angle=20°; slice thickness=5 mm, maximum C3 strength=293.9 mT/m³ with oscillation frequency of ω₀/2pi=5 kHz. Undersampling in the phase encoding direction was performed after acquisition during the image reconstruction by discarding echoes. All calculations were performed in MATLAB (MathWorks Inc, Natick, Massachusetts, USA). All reconstructions were performed via a conjugate gradient algorithm with 10 iterations using the GPU.

Results

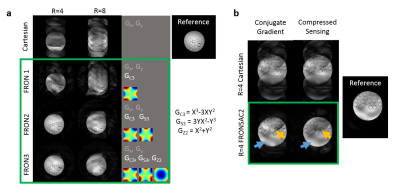
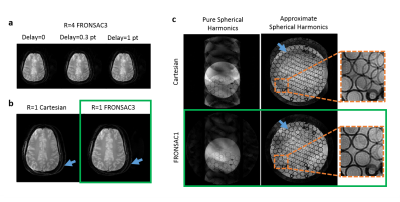
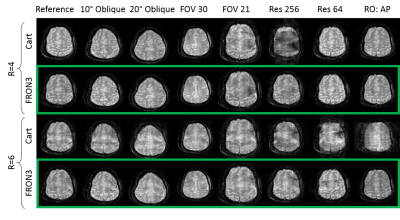
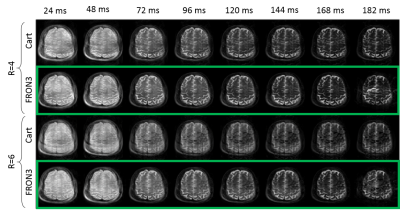
Figure 2a shows improving image quality as function of increasing NLG waveforms added to a Cartesian trajectory. The FRONSAC encoding reduces the undersampling artifact, particularly in the presence of 2 or more waveforms, which provide more degrees of freedom to manipulate the sampling function. Figure 2b shows the addition of NLGs in FRONSAC2 better condition the data for a compressed sensing approach, while no benefit is seen in under sampled Cartesian data. FRONSAC is resilient to experimental imperfections including timing errors (Figure 3a) and off-resonance spins (Figure 3b), and the resulting artifacts are indistinguishable from well-known and generally benign Cartesian artifacts. Field purity is also not required with this approach since the reduction in undersampling artifacts using an approximate C3 shape is similar to comparable pure C3 FRONSAC1 (Figure 3c). Figure 4 shows that once a FRONSAC NLG waveform has been well characterized by spatial and temporal mapping, it can be applied to a variety of different Cartesian scan prescriptions and still produce profound improvements in accelerated image quality. Figure 5 demonstrates that FRONSAC is synergistic with other acceleration strategies such as turbo spin echo (TSE) imaging and FRONSAC gradients do not interfere with the standard contrast.

Conclusion

FRONSAC represents highly effective general tool for increased spatial encoding efficiency that can lead to significant further reductions in scan times.

Acknowledgements

This works was funded by the National Institutes of Health under 5R01EB012289-04, 4R01 EB016978-04, K01EB168977 and R01EB022030. We would like to thank Andrew Dewdney, Keith Heberlein, and Rodney Mick from Siemens for hardware support. We would like to thank Stefan Kroboth for his help imaging with the Freiburg nonlinear gradient setup and Dr. Ying-Hua (Eva) Chu for providing the field camera and for support with the corresponding measurements. We would also like to thank Terry Nixon and Scott McIntyre for support with the Yale nonlinear gradient hardware.