0058
Diffusion interleaved and slice-shuffled (DiSS) imaging for joint diffusion-relaxometry studies1Biomedical Engineering, King's College London, London, United Kingdom, 2Centre for Medical Image Computing, University College London, London, United Kingdom
Synopsis
Imaging protocols that allow diverse contrast mechanisms to be sampled with different mixes open up exciting opportunities for joint modelling of tissue properties. However joint sampling with conventional sequence structures can be extremely inefficient and so prohibitively time consuming. Here we explore the joint inversion recovery-diffusion sampling challenge and create an efficient capability by breaking the “one-volume – one encoding” paradigm to interleave the diffusion encoding not per volume but for every slice. Flexible sampling during inversion recovery allowing sufficient samples for a joint fit to be acquired in a much shorter time. The approach has been tested in normal volunteer brain examinations.
Background
Combining diffusion and relaxometry measurements enables the multidimensional parameter space [T1,T2,ADC] to be explored in a novel way and delivers eloquent data for use with emerging multiparametric models. Efficient acquisitions are critical for integrated multiparametric imaging to achieve viable examination times. Moreover, spanning as much as possible of the parameter space within one acquisition has the potential to enhance internal consistency and motion robustness. Inversion-recovery DWI sequences using slice-shuffled (SS) techniques1-3 demonstrate the potential of this approach. These vary the order of slice acquisition to vary the slice inversion time (TI). However, current techniques typically still suffer from prohibitively long acquisition times. We have developed a diffusion-interleaved and slice-shuffled acquisition (DiSS) that can significantly accelerate combined measurements and offers increased flexibility to tune the parameter sampling density.Methods
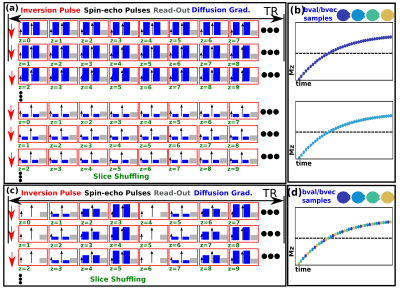
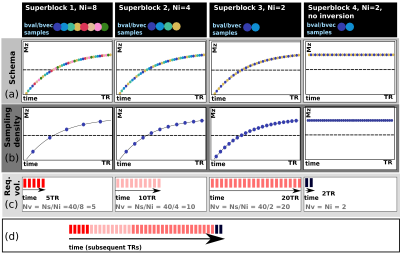
The conventional SS technique (as illustrated Fig. 1a) requires every slice (s=1,..,Ns) to be sampled with every TI for every diffusion encoding (d=1,..,Nd) - resulting in the acquisition of NsxNd volumes. This approach is extremely inefficient as the inversion recovery curve is generally massively oversampled: typical values of T1, TR and Ns (2s/6s/40 slices) lead to data points at 150msec intervals (Fig. 1b). More appropriate, sparser sampling is not possible with traditional “one volume–one diffusion encoding” schemes. Our approach breaks with this traditional paradigm by changing the diffusion encoding per slice4. By interleaving Ni diffusion encodings within the TR (Fig. 1c, Ni=4), multiple encoding combinations can be sampled within a single recovery curve (Fig 1d). Instead of repeating the same diffusion encoding with all Ns slice-shuffles, this technique only requires Ns/Ni repeats (we term this a superblock). As soon as a superblock is complete it is feasible to start a new superblock with a different choice of Ni. The final total acquisition will be made up by Nb (variable length) superblocks (Fig. 2d).
While the same TIs on the recovery curve are sampled in every super-block, varying the length Ni - and thus the number of combined encodings – allows different sampling densities as shown in Fig. 2 for Ni=8,4,2. Superblock size can for example be selected to balance the declining SNR at higher diffusion weightings, recognising that lower b-values can allow robust T1 estimation with fewer points on the recovery curve. Finally, superblocks without pre-inversion can be included into the sequence as shown in Fig. 2 (rightmost column) to achieve additional dMRI samples at a maximum data rate – these would, however, not be suitable for simple combined modelling approaches.
The described DiSS sequence was implemented on a Philips Achieva 3T-scanner. Brain data from 4 healthy volunteers was acquired using the 32ch-adult head coil. Various diffusion schemes were used, the data presented below was (protocol I:) 4 shells b0,b500,b1000,b1500 (1 direction) and (protocol II:) b0(3), b400(3) and b1000(6). Other parameters are TR/TE=6s/80ms, 2x2x2mm resolution, 40 slices, interleave factor Ni=4. The data was sorted to individual b-sample volumes and the phase of the complex data was corrected using a sliding-window filter to produce pure real signal images with noise in the Gaussian regime. Finally, the data was fit to a joint signal model to obtain PD, T1 and ADC. Additionally, T1 maps for each shell were computed.
Results
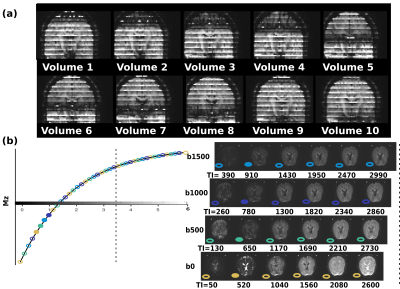
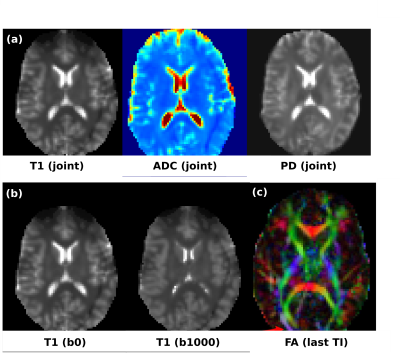
Fig. 3a shows the first superblock (10 volumes) of a DiSS dataset (10 volumes), illustrating the varying TIs and interleaved b-values. Fig. 3b shows exemplary slices with their corresponding TIs and b-values. Fig 4a shows the obtained PD, T1, ADC for the joint fit; Fig. 4b shows the T1 maps for b0/b1000 and 4c the fractional anisotropy (FA) map at longest TI. The estimates of the joint fit are within the expected parameter range. The independent estimates of T1 per shell illustrate a T1-dependence of restricted diffusion compartments, which dedicated multi-compartment models can probe in multi-dimensional parameter space1,2. For protocol II, for the given parameters (Ns=40 and TR6s) a conventional SS acquisition would require 12(encodings)x40(slices) volumes resulting in a total acquisition time of 16min - reduced by DiSS to 4min.Discussion and Outlook
The flexible nature of the proposed approach allows the acquisition parameters (interleaving factor, superblocks) to be tuned to the expected SNR and range of parameter variation. An additional benefit is that mixing the diffusion weighting shot-by-shot can dramatically decrease the thermal demands on the gradient system, allowing more efficient operation4. DiSS combines effortlessly with acceleration technique such as SENSE/Half-scan as the proposed conceptual change is independent of the individual EPI read-out. Combination with simultaneous slice imaging techniques is also a straightforward means to further increase coverage. Future work will focus on deploying the DiSS approach for in-depth brain studies. In particular, this novel accelerated acquisition ideally lends itself to bespoke multi-compartment models to disentangle myelin and axonal compartments.Acknowledgements
This work received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/20072013)/ERC grant agreement no. 319456 (dHCP project), the NIH Human Placenta Project grant 1U01HD087202-01, the Wellcome Trust (Sir Henry Wellcome Fellowship, 201374/Z/16/Z) and was supported by the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z), MRC strategic grant MR/K006355/1 and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.References
1. De Santis S, Barazany D, Jones DK, Assaf Y. Resolving relaxometry and diffusion properties within the same voxel in the presence of crossing fibres by combining inversion recovery and diffusion-weighted acquisitions. Magnetic Resonance in Medicine. 2016;75(1):372-380. doi:10.1002/mrm.25644.
2. De Santis S, Assaf Y, Jeurissen B, Jones DK, Roebroeck A. T1 relaxometry of crossing fibres in the human brain. Neuroimage. 2016;141:133-142. doi:10.1016/j.neuroimage.2016.07.037.
3. Hua Wu, Qiyuan Tian, Christian Poetter, Kangrong Zhu, Matthew J Middione, Adam B Kerr, Jennifer A McNab, and Robert F Doughert, Whole Brain Inversion Recovery Diffusion Weighted Imaging Using Slice-Shuffled Acquisition ISMRM 2017, 0387
4. Hutter, J., Christiaens, D., Kuklisova-Murgasova, M., Cordero-Grande, L., Slator, P., Price, A., Rutherford, M., Hajnal, J. V , Dynamic field mapping and motion correction using interleaved double spin-echo diffusion MRI, 2017, Lecture Notes in Computer Science - MICCAI 2017, Vol. 10433 LNCS, 523-531
Figures