0036

Super-resolution for spherical deconvolution of multi-shell diffusion MRI data
Ben Jeurissen1, Gabriel Ramos-Llordén1, Floris Vanhevel2, Paul M Parizel2, and Jan Sijbers1

1imec-Vision Lab, Dept. of Physics, University of Antwerp, Antwerp, Belgium, 2Dept. of Radiology, Antwerp University Hospital and University of Antwerp, Antwerp, Belgium

Synopsis

Multi-tissue constrained spherical deconvolution (MT-CSD) can simultaneously estimate the full white matter fiber orientation distribution function (fODF) and the apparent densities of cerebrospinal fluid and grey matter from multi-shell diffusion MRI data, making it an attractive option for clinical and neuroscientific studies. Unfortunately, MT-CSD at high spatial resolution is challenging due to scan time and signal-to-noise ratio constraints. We propose a new MT-CSD approach that enables super-resolution estimation from multiple thick-sliced data sets with varying slice orientation. Using data acquired on a clinical scanner, we demonstrate high-quality tissue density maps and fODFs at 1×1×1mm3 spatial resolution in under 10 minutes.

Introduction

Multi-tissue constrained spherical deconvolution (MT-CSD)1 of multi-shell diffusion MRI (dMRI) data allows simultaneous estimation of the full white matter (WM) fiber orientation distribution function (fODF) and the apparent densities of cerebrospinal fluid (CSF) and gray matter (GM). Despite the potential of MT-CSD, clinical scans are limited in spatial resolution due to constraints on scan time and signal- to-noise ratio (SNR). Currently, obtaining images covering the whole brain with a clinical scanner within a reasonable time for routine use, limits the resolution to approximately 2 mm cubed; to characterise the fine structures of the WM, and particularly the intricate folding patterns of the cortical surface, a higher resolution is required. To address this issue, we propose a new super-resolution approach for high-resolution MT-CSD, within clinically feasible acquisition times and with adequate SNR.

Methods

MT-CSD at native resolution: MT-CSD is typically performed voxel-wise and can be formulated as a constrained linear least squares problem of the form1:

$$\hat{\mathbf{x}}=\text{arg}\min\limits_{\mathbf{x}}\,\lVert\mathbf{C}\mathbf{x}−\mathbf{y}\rVert_2^2\quad\text{subject to}\quad\mathbf{A}\mathbf{x}\ge\mathbf{0}$$

where $$$\mathbf{C}$$$ is the forward spherical convolution matrix relating the vectors of unknown multi-tissue fODF spherical harmonic (SH) coefficients, $$$\mathbf{x}$$$, to the vector of measured dMRI signal intensities, $$$\mathbf{y}$$$; and $$$\mathbf{A}$$$ is the constraint matrix relating the multi-tissue fODF SH coefficients $$$\mathbf{x}$$$ to their amplitudes, effectively imposing non-negativity of the tissue densities.

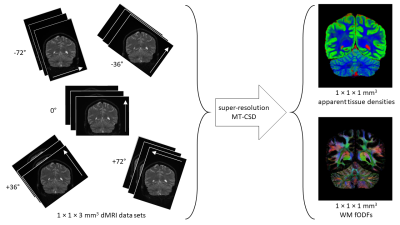
Super resolution reconstruction: Super-resolution reconstruction is the process of producing a high-resolution image from a sequence of low-resolution images, where each low-resolution image samples the high-resolution scene in a distinct fashion2. In the context of dMRI, acquiring data with thick slices, results in reduced acquisition time and increased SNR; the loss of resolution along the slice direction can be recovered by combining multiple thick-sliced data sets with different slice orientations using super-resolution reconstruction3,4 (see Fig. 1).

Super-resolution MT-CSD: The above equation can be extended to support volume-wise super-resolution estimation of multi-tissue fODFs as follows:

$$\hat{\mathbf{x}}^\prime=\text{arg}\min\limits_{\mathbf{x^\prime}}\,\lVert\mathbf{S}\mathbf{C}^\prime\mathbf{x}^\prime−\mathbf{y}^\prime\rVert_2^2\quad\text{subject to}\quad\mathbf{A}^\prime\mathbf{x}^\prime\ge\mathbf{0}$$

where $$$\mathbf{C}^\prime$$$ is the volume-wise forward convolution matrix and $$$\mathbf{S}$$$ is the super-resolution sampling matrix, relating the signal intensities expected in all high-resolution voxels to the acquired signal intensities in all low-resolution voxels, $$$\mathbf{y}^\prime$$$; and $$$\mathbf{A}^\prime$$$ is the volume-wise constraint matrix. The super-resolution matrix $$$\mathbf{S}$$$ takes into account motion, geometric transformation, blurring, and down-sampling and is implemented efficiently using a set of shear transformations5. The sheer size of the problem and constraint matrices precludes the use of standard quadratic programming solvers. Instead, we employ a majorize-minimize algorithm to decouple the voxel-wise constrained spherical deconvolution problem from the volume-wise super resolution problem6. To improve the conditioning of the super-resolution problem without blurring fine details, we complement the above equation with a small total variation penalty.

Acquisition: 5 dMRI data sets with high in-plane resolution and thick slices (voxel size 1×1×3mm3) were acquired on a 3T MAGNETOM Prisma with a 32-channel head coil array (Fig.1). Each data set was acquired with a unique slice orientation = [-72°,-36°,0°,36°,72°], and a unique set of 26 q-space samples (b = [0,700,1200,2800] s/mm2, distributed over 2, 3, 8 and 13 directions, respectively)7, resulting in a total of 130 unique q-space samples (TR/TE = 4300/90 ms/ms, partial-Fourier = 6/8, iPAT = 2 (GRAPPA), SMS = 2, and bandwidth = 1196 Hz/pix). Total acquisition time was just under 10 minutes.

Results and discussion

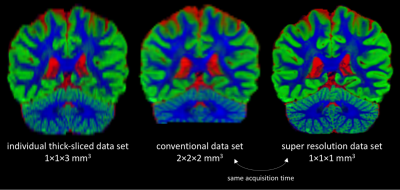
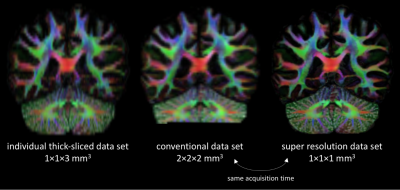
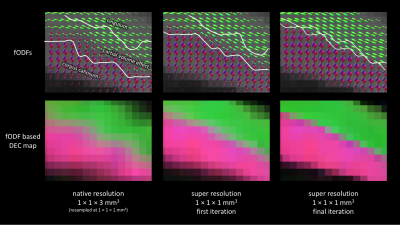
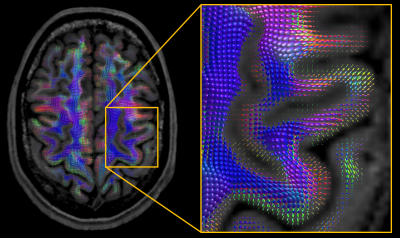
Figs. 2-3 demonstrate that super-resolution MT-CSD can recover the fine details lost due to the thick-sliced acquisition and that its spatial resolution clearly exceeds that of a conventional direct 2×2×2mm3 acquisition obtained within the same time. This is the case in terms of tissue type discrimination (Fig. 2) as well as in terms of fiber bundle discrimination within WM (Fig. 3). The ability to super-resolve distinct fiber bundles is further demonstrated in Fig. 4: our approach can significantly reduce the partial volume effect between interfacing fiber bundles (e.g. between the corpus callosum and the cingulum bundle). In Fig. 5 we show the fODFs in the cortical folds as obtained with the proposed approach. Note the clean radial organization of the fODFs, typically observed in high-resolution scans obtained with bespoke scanners and lengthy acquisitions8,9.

Conclusion

We have extended the MT-CSD approach with super-resolving capabilities, allowing high-resolution multi-tissue fODFs to be estimated from multiple low resolution scans. Using a clinical scanner, we have demonstrated the method's ability to obtain high quality fODFs and tissue density maps at 1×1×1mm3 resolution in under 10 minutes. The proposed framework is scalable: it can handle extremely large data sets; and flexible: it can accommodate for motion, arbitrary slice orientations, different voxel sizes10, and multiple shells and tissue types.

Acknowledgements

BJ is a postdoctoral fellow of the Research Foundation Flanders, Belgium (FWO: 12M3116N).

References

1. Jeurissen, B., Tournier, J.-D., Dhollander, T., Connelly, A. & Sijbers, J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. Neuroimage 103, 411–426 (2014).

2. Greenspan, H., Oz, G., Kiryati, N. & Peled, S. MRI inter-slice reconstruction using super-resolution. Magn. Reson. Imaging 20, 437–446 (2002).

3. Scherrer, B., Gholipour, A. & Warfield, S. K. Super-resolution reconstruction to increase the spatial resolution of diffusion weighted images from orthogonal anisotropic acquisitions. Med. Image Anal. 16, 1465–1476 (2012).

4. Van Steenkiste, G. et al. Super-resolution reconstruction of diffusion parameters from diffusion-weighted images with different slice orientations. Magn. Reson. Med. 75, 181–195 (2016).

5. Poot, D. H. J., Van Meir, V. & Sijbers, J. General and efficient super-resolution method for multi-slice MRI. Med. Image Comput. Comput. Assist. Interv. 13, 615–622 (2010).

6. Muckley, M. J., Noll, D. C. & Fessler, J. A. Fast parallel MR image reconstruction via B1-based, adaptive restart, iterative soft thresholding algorithms (BARISTA). IEEE Trans. Med. Imaging 34, 578–588 (2015).

7. Caruyer, E., Lenglet, C., Sapiro, G. & Deriche, R. Design of multishell sampling schemes with uniform coverage in diffusion MRI. Magn. Reson. Med. 69, 1534–1540 (2013).

8. Uğurbil, K. et al. Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. Neuroimage 80, 80–104 (2013).

9. Calamante, F., Jeurissen, B., Smith, R. E., Tournier, J.-D. & Connelly, A. The role of whole-brain diffusion MRI as a tool for studying human in vivo cortical segregation based on a measure of neurite density. Magn. Reson. Med. (2017). doi:10.1002/mrm.26917

10. Sotiropoulos, S. N. et al. RubiX: combining spatial resolutions for Bayesian inference of crossing fibers in diffusion MRI. IEEE Trans. Med. Imaging 32, 969–982 (2013).

11. Dhollander, T., Smith, R. E., Tournier, J. D., Jeurissen, B. & Connelly, A. Time to move on: an FOD-based DEC map to replace DTI’s trademark DEC FA. in Proc. Intl. Soc. Mag. Reson. Med. 23, 1027 (2015).

Figures

Fig. 1: From multiple dMRI data sets with high in-plane resolution and low through-plane resolution and rotated slice orientations (left), super resolution MT-CSD directly estimates apparent tissue densities and WM fODFs at high spatial resolution, both in-plane and through-plane (right). Slice orientations are indicated with white arrows.

Fig. 2: Apparent CSF/GM/WM density maps obtained with MT-CSD at native resolutions and using super resolution. Note that the super-resolution approach (right) can recover the fine details lost due to acquiring thick slices (left). It is also evident that the super-resolution approach outperforms MT-CSD at native 2×2×2 mm3 resolution obtained within the same acquisition time.

Fig. 3: WM-fODF based directionally-encoded color (DEC) maps11 obtained with MT-CSD at native resolutions (left, middle) and using super resolution (right). Note that the super-resolution approach (right) is characterized by much sharper transitions between different fiber bundles than the MT-CSD maps at native resolution. Super-resolution capabilities within WM are demonstrated in more detail in Fig. 4.

Fig. 4: Super-resolving capabilities within WM demonstrated at the interface between the corpus callosum and the cingulum bundle (sagittal view): fODFs (top row) and fODF-based DEC maps (bottom row). At native resolution (left column), the region containing bimodal fODFs (outlined using white lines) spans roughly 4-7 high-resolution voxels, resulting in a blurred edge in the DEC map. After the first super-resolution iteration (center column), the overlap has shrunk to 3-5 voxels. After convergence (right column), corpus callosum and cingulum bundle are almost completely separated with only 1-2 voxels of overlap, resulting in a sharp edge in the DEC map.

Fig. 5: WM fODFs in the cortical folds obtained with super-resolved MT-CSD imposed on a T1-weighted image. Note the high degree of spatial consistency of the fODFs as well as the consistent radial pattern of fibers observed in the cortex.

Proc. Intl. Soc. Mag. Reson. Med. 26 (2018)
0036