0032
5D Flow MRI – Respiratory Motion Resolved Accelerated 4D Flow Imaging Using Low-Rank + Sparse Reconstruction1ETH Zurich, Zurich, Switzerland
Synopsis
We present a low-rank + sparse reconstruction method which resolves respiratory motion in 4D flow magnetic resonance imaging as a low-rank signal component. Respiratory motion resolved 4D flow MRI data is reconstructed and compared to the total variation based XD-GRASP method and a standard parallel imaging acquisition protocol. Good agreement of the reconstructed results with the reference shows that a low-rank model is effective in resolving respiratory motion in 4D flow magnetic resonance imaging.
Introduction
Respiratory motion resolved 4D flow magnetic resonance imaging1 promises increased scan efficiency and valuable physiological information in various congenital diseases such as the Fontan circulation2.
Respiratory motion-resolved MR imaging frameworks3,4 acquire data continuously throughout the respiratory cycle with subsequent binning of the data into discrete respiratory motion states. In reconstruction, redundancies between different motion states are exploited to improve reconstruction accuracy. Typically, correlation among neighboring respiratory motion states is exploited by penalizing total variation (TV) along the respiratory motion dimension in an iterative image reconstruction approach4,5. However, penalizing finite differences on a relatively coarse resolution can lead to underestimation of velocities in 4D flow MRI6.
The objective of the present study is to propose 5D Flow MRI based on resolving respiratory motion as a low-rank component in a low-rank + sparse (L+S)7 reconstruction and compare it to XD-GRASP and a standard respiratory-gated parallel imaging protocol.
Methods
Using the insight that 4D flow data can be well represented as the sum of a low-rank component and a sparse component in the Hadamard transform domain8, the approach is extended here to include the respiratory motion dimension. The corresponding minimization problem reads as follows:
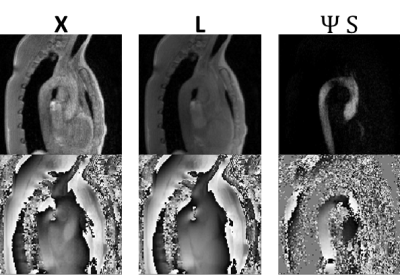
$$\underset{L,S}{\operatorname{argmin}} ||\Omega\mathcal{F} \mathcal{S}(L+S)-y||_2^2 +\lambda_L||L||_*+\lambda_S||\Psi S||_1, \> s.t. X=L+S $$Where $$$\Omega,\mathcal{F},\mathcal{S}$$$ denote the undersampling operator, Fourier transform and sensitivity maps, respectively. $$$X\in \mathbf{C}^{N_x \times N_{hp} \times N_{ms} \times N_{k_v} }$$$ denotes the image tensor with spatial locations, heart phases, respiratory motion states and velocity encodings. $$$L$$$ and $$$S$$$ refer to the low-rank and sparse component, respectively. For the low-rank regularization, $$$L$$$ is reordered as a Casorati matrix $$$L\in \mathbf{C}^{N_x \times N_{hp} N_{ms} N_{k_v} }$$$. $$$\Psi$$$ is the Hadamard matrix [+1 +1 +1 +1;+1 +1 -1 -1; +1 -1 +1 -1;+1 -1 -1 +1], i.e. the differences between the different velocity encodings are used as sparse representation. An illustration of the L+S decomposition with Hadamard sparsity is provided in Figure 1.
Data acquisition
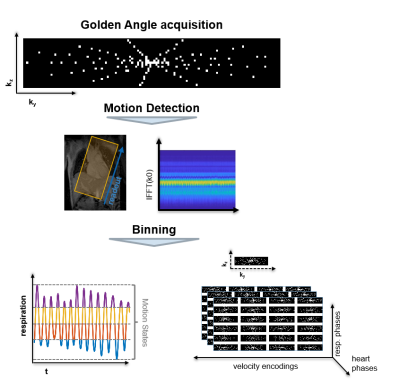
4D Flow data in the aortic arch of a healthy volunteer was acquired on a 3T Philips Ingenia system (Philips Healthcare, Best, the Netherlands) using a Cartesian four-point phase-contrast gradient-echo sequence with uniform venc of 220 cm/s, a spatial resolution of 2.5x2.5x2.5 mm3 and 16 cardiac phases. The measurement was performed with a 28 channel receiver coil which was compressed to 5 virtual channels9.
The acquisition process is illustrated in Figure 2. The measured data were binned into 4 different respiratory motion states with equal acceleration factors of approximately 7 per bin. For comparison, a standard 4D Flow MRI protocol using SENSE10 with an acceleration factor of 2 and using a 5 mm navigator window was obtained.
Data reconstruction
Coil sensitivity maps were calculated from a separate calibration scan using ESPIRiT11. The SENSE scan was reconstructed with Tikhonov regularization and using the same sensitivity maps as used in the CS reconstructions. XD-GRASP and SENSE reconstructions were performed using the Berkeley Advanced image Reconstruction Toolbox12. L+S reconstruction was implemented in Python 2.7.12. The regularization parameters were automatically determined based on the minimum deviation of velocities in the ascending aorta relative to the standard SENSE reconstruction. Concomitant field correction was applied to the signal phase according to13 and eddy currents were corrected for with a linear model fitted to stationary tissue14.
Data analysis
Results were compared using GTFlow (Gyrotools LLC, Zurich, Switzerland). Velocities were calculated for a plane in the ascending aorta. Velocity magnitude images and streamline visualizations were assessed qualitatively.
Results
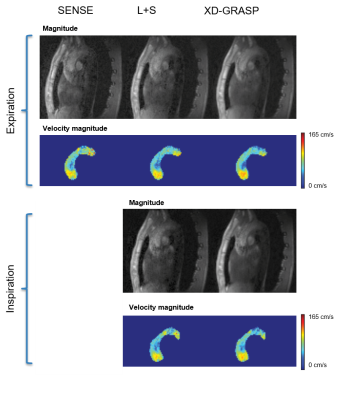
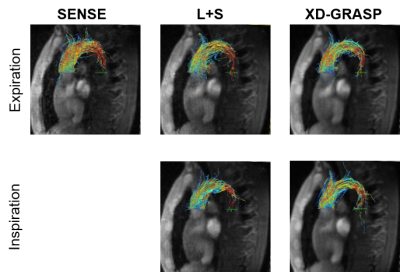
Exemplary velocity magnitude and magnitude images are shown in Figure 3. L+S and XD-GRASP provide similar results in terms of magnitude and phase images (Figure 3). Through-plane velocities and velocity components in systole are compared in Figure 4 for both, inspiration and expiration. Velocities encoded in the in foot-head(FH) direction are well recovered by all methods, whereas some artifacts can be observed in the right-left(RL) direction. Streamline visualizations in systole for inspiration and expiration show similar flow fields for the different methods (Figure 5).Discussion
A framework for 5D Flow MRI was implemented with L+S and XD-GRASP and its feasibility tested in-vivo. Both methods show good agreement in terms of velocity profiles and maps with the standard 4D Flow MRI protocol, however permit 3.5x faster acquisition and resolve the respiratory dimension in addition. Further in-vivo experiments are warranted to test for significant differences between L+S and XD-GRASP.
In this work, similar flow fields were reconstructed in inspiration and expiration which can be expected for aortic flow. Future investigations will be aimed at studying venous flow and its dependency on the respiratory state15. To this end, the acquisition framework has to be extended to include a multi-venc encoding scheme16, in order to provide sufficient velocity-to-noise ratio for low velocities.
Acknowledgements
The authors thank Giuseppe Valvano for his valuable advice regarding the L+S algorithm and Richard Droste for contributing to initial experiments.References
[1] J. Y. Cheng, T. Zhang, M. T. Alley, M. Uecker, M. Lustig, J. M. Pauly, and S. S. Vasanawala, “Comprehensive multi-dimensional MRI for the simultaneous assessment of cardiopulmonary anatomy and physiology,” Sci. Rep., vol. 7, no. 1, p. 5330, 2017.
[2] M. Gewillig, “The Fontan circulation,” Heart, vol. 91, no. 6, pp. 839–846, 2005.
[3] A. Sigfridsson, L. Wigström, J. P. E. Kvitting, and H. Knutsson, “k-t2 BLAST: Exploiting spatiotemporal structure in simultaneously cardiac and respiratory time-resolved volumetric imaging,” Magn. Reson. Med., vol. 58, no. 5, pp. 922–930, 2007.
[4] L. Feng, L. Axel, H. Chandarana, K. T. Block, D. K. Sodickson, and R. Otazo, “XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing,” Magn. Reson. Med., vol. 75, no. 2, pp. 775–788, 2016.
[5] S. S. Cheng, Joseph Y., Zhang, Tao, Alley, Marcus T., Lustig, Michael, Pauly, John M., Vasanawala, “Ultra-High-Dimensional Flow Imaging (N-D Flow),” in ISMRM 2016, 2016.
[6] C. Santelli, M. Loecher, J. Busch, O. Wieben, T. Schaeffter, and S. Kozerke, “Accelerating 4D Flow MRI by Exploiting Vector Field Divergence Regularization.”
[7] D. K. Sodickson, R. Otazo, and E. Candes, “Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components,” vol. 1136, pp. 1125–1136, 2015.
[8] G. Valvano, N. Martini, A. Huber, C. Santelli, C. Binter, D. Chiappino, L. Landini, and S. Kozerke, “Accelerating 4D flow MRI by exploiting low-rank matrix structure and hadamard sparsity,” Magnetic Resonance in Medicine, no. September, pp. 1–12, 2016.
[9] T. Zhang, J. M. Pauly, S. S. Vasanawala, and M. Lustig, “Coil compression for accelerated imaging with Cartesian sampling,” Magn. Reson. Med., vol. 69, no. 2, pp. 571–582, 2013.
[10] K. P. Pruessmann, M. Weiger, M. B. Scheidegger, and P. Boesiger, “SENSE: Sensitivity encoding for fast MRI,” Magn. Reson. Med., vol. 42, no. 5, pp. 952–962, 1999.
[11] M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, and M. Lustig, “ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA,” Magn. Reson. Med., vol. 71, no. 3, pp. 990–1001, 2014. [12] F. Ong, M. Uecker, U. Tariq, A. Hsiao, M. T. Alley, S. S. Vasanawala, and M. Lustig, “Berkeley advanced reconstruction toolbox,” Magn. Reson. Med., vol. 73, no. 2, pp. 828–842, 2015.
[13] M. A. Bernstein, X. J. Zhou, J. A. Polzin, K. F. King, A. Ganin, N. J. Pelc, and G. H. Glover, “Concomitant gradient terms in phase contrast MR: Analysis and correction,” Magn. Reson. Med., vol. 39, no. 2, pp. 300–308, 1998.
[14] P. G. Walker, G. B. Cranney, M. B. Scheidegger, G. Waseleski, G. M. Pohost, and A. P. Yoganathan, “Semiautomated method for noise reduction and background phase error correction in MR phase velocity data,” J. Magn. Reson. Imaging, vol. 3, no. 3, pp. 521–530, 1993.
[15] F. K. Nakhjavan, W. H. Palmer, and M. Mcgregor, “Influence of respiration on venous return in pulmonary emphysema,” Circulation, vol. 33, no. 1, pp. 8–16, 1966.
[16] C. Binter, V. Knobloch, R. Manka, A. Sigfridsson, and S. Kozerke, “Bayesian multipoint velocity encoding for concurrent flow and turbulence mapping,” Magn. Reson. Med., vol. 69, no. 5, pp. 1337–1345, 2013.
[17] J. Y. Cheng, K. Hanneman, T. Zhang, M. T. Alley, P. Lai, J. I. Tamir, M. Uecker, J. M. Pauly, M. Lustig, and S. S. Vasanawala, “Comprehensive motion-compensated highly accelerated 4D flow MRI with ferumoxytol enhancement for pediatric congenital heart disease,” J. Magn. Reson. Imaging, vol. 43, no. 6, pp. 1355–1368, 2016.
[18] S. Wundrak, J. Paul, J. Ulrici, E. Hell, and V. Rasche, “A small surrogate for the golden angle in time-resolved radial MRI based on generalized fibonacci sequences,” IEEE Trans. Med. Imaging, vol. 34, no. 6, pp. 1262–1269, 2015. [19] T. Zhang, J. Y. Cheng, Y. Chen, D. G. Nishimura, J. M. Pauly, and S. S. Vasanawala, “Robust self-navigated body MRI using dense coil arrays,” Magn. Reson. Med., vol. 76, no. 1, pp. 197–205, 2016.
Figures