0001
Non-invasive pressure estimations by virtual fields – cardiovascular pressure drops from 4D flow MRI1Department of Medical Engineering, KTH Royal Institute of Technology, Stockholm, Sweden, 2Clinical Sciences, Karolinska Institutet, Stockholm, Sweden, 3Division of Imaging Sciences and Biomedical Engineering, King's College London, London, United Kingdom, 4Department of Congenital Heart Disease, Evelina Children’s Hospital, London, United Kingdom, 5Departments of Surgery and Biomedical Engineering, University of Michigan, Ann Arbor, MI, United States, 6Department of Clinical Science, Intervention and Technology (CLINTEC), Karolinska Institutet, Stockholm, Sweden
Synopsis
4D-flow-MRI enables the non-invasive assessment of cardiovascular pressure drops; however, estimation accuracy depends on vascular topology and acquisition noise. Here, we present a method that minimizes the impact of these by using virtual fields to isolate and probe hemodynamic pressure drops. We show that, in-silico, the method accurately assesses pressure drops over multiple segments of a patient-specific co-arcted aorta (average error below 22%), independent of anatomical bifurcations. Additionally, the method compares successfully against catheter measurements, using 4D-flow-MRI in-vivo (average error at peak systole below 15%). With this, the method represents a refined tool for hemodynamic analysis of cardiovascular flow.
Introduction
The development of 4D-flow-MRI has enabled non-invasive studies of intravascular flow1. With regional pressure drops shown to be a biomarker for many cardiovascular pathologies2-3, methods have been proposed to derive this from 4D-flow-MRI data4-7. Even though accurate in investigated setups4-6, available techniques still have difficulties in-vivo, where complex anatomies and clinical noise levels are present. To overcome these, we present a method using the concept of virtual fields8 and work-energy equations6 to derive relative pressure drops from acquired flow. Using virtual fields, hemodynamic pressure losses can be probed in any given vascular segment, regardless of anatomical complexity or flow behavior.Method
The proposed method originates from a work-energy formulation assessing relative pressure drops from a flow field, $$$v$$$6. Here we propose an alteration by introducing a virtual field, $$$w$$$, analyzing the virtual work of $$$w$$$ within a vascular domain in order to isolate the pressure drop, $$$\Delta p$$$. By so, influence from measurement inaccuracies, low flow magnitudes or bifurcations associated with $$$v$$$ are minimized.
Here, $$$w$$$ is chosen as the solution to a Stokes flow boundary value problem, with flow permitted over the inlet and outlet of the desired pressure drop, and with flow restricted at any other surface (vascular wall or secondary bifurcations). Using our previously proposed derivation6 in conjuction with $$$w$$$, $$$\Delta p$$$ can be identified by:
$$ \Delta p=-\frac{1}{Q_w} \left(\frac{\partial}{\partial t}K_w + A_w + V_w \right) $$
with $$$K_w$$$, $$$A_w$$$, and $$$V_w$$$ being the kinetic, advective, and viscous energy components when using $$$w$$$ as the weighting velocity field, and $$$Q_w$$$ being the flow of $$$w$$$ over the domain inlet (for details, see6).
To assess method performance, two setups are evaluated. First, a challenging patient-specific in-silico model of a co-arcted aorta9 is used to generate simulated image data (spatial/temporal resolution: 2 mm3, 43 ms, SNR: 10 and 30), with temporal pressure drops compared to the simulated pressure fields. Second, 4D-flow-MRI (Philips Achieva, 1.5T, spatial/temporal resolution: 2.1 mm3, 31 ms) is acquired from 6 adolescent Fontan patients, with $$$v$$$ reconstructed and corrected using GTFlow (GyroTools). Flow-field-based pressure drop estimates are compared against invasive catheter measurements acquired during the same imaging session. $$$w$$$ is solved using a finite-difference scheme on the vascular segment of interest using a right-preconditioned iterative GMRES-solver and a BFBT-preconditioner10-11. Spatial and temporal noise filtering is introduced by polynomial interpolation and frequency-domain low-pass filtering, respectively.
Results
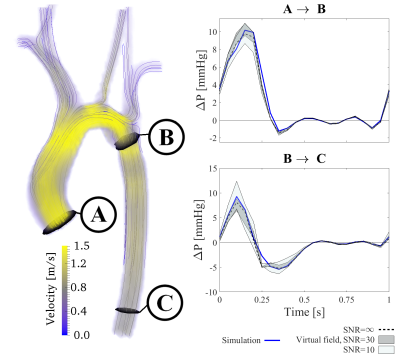
Figure 1 shows the results of the in-silico setup. The method estimation follows the true pressure drop throughout the cardiac cycle, with minor noise-levels differences. Specifically, the pressure drop is captured with an average error of 22%, equaling 1.9 mmHg at peak systole. Importantly, the strength of the method is shown in the preserved accuracy from aortic inlet to coarctation, unaffected by the bifurcations along the aortic arch, or of the diastolic low-magnitude-flows.
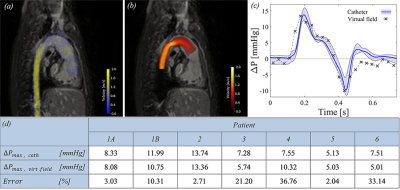
Figure 2 summarizes the results of the in-vivo setup. Again, the method captures temporal changes in relative pressure, with the virtual field isolating the vascular region-of-interest. The peak systolic pressure is captured with an average error of 15%, corresponding to an accuracy of 1.3 mmHg. The method seems robust to anatomical bifurcations or low-magnitude-flows, even though minor fluctuations seem visible in certain phases.
For both setups, our method performs favorable to conventional Bernoulli-based estimates as well as to previous work-energy based measures6 (average error above 200%), in part due to that these methods are not developed to handle vascular bifurcations or diastolic flow-magnitudes.
Discussion
The correspondence between gold-standard-measures in both in-silico and in-vivo setups demonstrates the method accuracy. The ability to probe segments spanning over several bifurcations without significant deterioration is a particular strength. Additionally, the robustness against image noise is an important improvement on previous methods, originating from the ability to control the accuracy of the virtual field. Method refinements can though be foreseen, with simplified extensions to limited flow acquisitions (such as 2D PC-MRI) or by the incorporation of turbulent kinetic energy. Additionally, evaluation on a larger cohort group could further clarify the abilities of the method. With that, the method is currently being applied on a clinical patient cohort, in order to evaluate the value of refined pressure probing in vascular domains inaccessible by previous methods.Conclusion
Using virtual fields, we show that hemodynamic pressure drops can be successfully assessed from 4D-flow, taking into account anatomical bifurcations, low-flow-phases, and realistic noise-levels. Using our method, pressure-drop estimations can accurately and robustly be performed in potentially any given vascular segment, given sufficient sampling and noise-level. With such, the method provides clinicians and researchers with a refined tool for hemodynamic pressure-drop analysis.Acknowledgements
We would like to acknowledge funding from Engineering and Physical Sciences Research Council (EP/N011554/1). D.L. was financially supported by the Hans Werthén foundation of The Royal Swedish Academy of Engineering Sciences (IVA), Gålöstiftelsen, and the Erik and Edith Fernström Foundation for Medical Research. This work was also supported by the Wellcome EPSRC Centre for Medical Engineering at King’s College London (WT 203148/Z/16/Z).References
1. Stankovic Z, Allen BD, Garcia J, Jarvis KB, Markl M. 4D flow imaging with MRI. Cardiovasc Diagn Ther. 2014;4(2):173-92.
2. Baumgartner H, Hung J, Bermejo J, Chambers JB, Evangelista A, et al. Echocardiographic assessment of valve stenosis: EAE/ASE recommendations for clinical practice. J. Am. Soc. Echocardiogr. 2008:101-102
3. Vahanian A, Baumgartner H, Bax J, Butchart E, Dion R, et al. Guidelines on the management of valvular heart disease: the task force on the management of valvular heart disease of the european society of cardiology. Eur. Heart J. 2007:28(2):230-68
4. Ebbers T, Wigström L, Bolger AF, Engvall J, Karlsson M. Estimation of relative cardiovascular pressure using time-resolved three-dimensional phase contrast MRI. Magn Res Medicine. 2001:45(5):872-79
5. Krittian SBS, Lamata P, Michler C, Nordsletten DA, Bock J, et al. A finite-element approach to the direct computation of relative cardiovascular pressure from time-resolved MR velocity data. Med. Image Anal. 2012:16(5):1029-37
6. Donati F, Figueroa CA, Smith NP, Lamata P, Nordsletten DA. Non-invasive pressure difference estimation from PC-MRI using the work-energy equation. Med. Image Anal. 2015:26(1):159-72
7. Donati F, Myerson S, Bissell MM, Smith NP, Neubauer S, et al. Beyond Bernoulli: Improving the accuracy and precision of noninvasive estimation of peak pressure drops. Circ Cardiovasc Im. 2017:10(1):e005207
8. Maugin GA. The method of virtual power in continuum mechanics: application to coupled fields. Acta Mechanica. 1980:35(1-2):1-70
9. Sotelo J, Valverde I, Beerbaum P, Greil G, Schaeffter T, et al. Pressure gradient prediction in aortic coarctation using a computational-fluid-dynamics model: validation against invasive pressure catheterization at rest and pharmacological stress. J. Cardiovasc. Magn. Reson. 2015:17(Suppl. 1):Q78
10. Elman H, Howle VE, Shadid J, Shuttleworth R, Tumarino R. Block preconditioners based on approximate commutators. SIAM J Sci Comp. 2006:27(5):1651-68
11. Saad Y, Schultz MH. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J Sci and Stat Comput. 1986:7(3):856-69
Figures