Synopsis

Analytical solutions provide sound insight in the Bloch-McConnell equations that underlie every exchange-weighted contrast, be it CEST, T1p or T2. In this lecture we show that for all experiment affecting the water magnetization, a single eigenvalue solution is able to describe all these experiments. This knowledge forms the basis for interpretation of the outcomes of different exchange-weighted contrasts as well as quantification of exchange.

Purpose

Bloch-McConnell-Theory

In the rotating frame of reference (x, y, z) defined by the frequency ω_rf of the oscillating field B₁(t), the Bloch-McConnell equations for two pools, water (pool a), CEST (pool b) with the combined magnetization vector M read

$$\frac{\text{d}}{\text{d}t}\overrightarrow{M}=A\cdot\overrightarrow{M}+\overrightarrow{C}$$

Where the matrix A contains all terms for rotation (ω1, Δω), relaxation (R₁,R₂) within the pools, and exchange between the pools (k_ba, k_ab=f_bk_ba), with the pool size fraction f_b=M_0b/M_0a.

The vector C contains the M₀ magnetization and leads to a recovery to thermal M₀>0.

For a single pool the dynamic of the free Bloch equations (Δω=- ω₀ , ω₁=0) is well known: The longitudinal magnetization will recover along the B₀ field with the rate R_1a. The transversal magnetization will rotate around the Z-axis with the Larmor frequency ω0. Going from the Bloch equations to the Bloch-McConnell equations¹ of a two pool system of water pool (a) and CEST pool (b) directly shows that the T₁ and T₂ relaxation will be altered. Reorganization of the terms already shows a first order estimation R₁=R_1a+k_ab and R₂=R_2a+k_ab.

Eigenspace solutions

In detail the eigenvalues of the system have to be solved which leads to the observed longitudinal relaxation rate:

$$R_{1obs}\approx\frac{R_{1a}+f_bR_{1b}}{1+f_b}$$

(The second eigenvalue is a fast relaxation that can be observed in WEX experiments².)

And the observed transversal relaxation rate (Swift-Connick relation³)

$$R_{2obs}= R_{2a}+f_bk_b\frac{\delta\omega_b^2+R_{2b}(R_{2b}+k_b)}{(R_{2b}+k_b)^2+\delta\omega_b^2}$$

This already shows that magnetization transfer between exchanging pools can be understood and described by relaxation theory. We consider now the driven Bloch equations (Δω, ω₁>0), but first again a single pool. The dynamic behavior is actually very similar: In the rotating frame of reference, we have again longitudinal relaxation R1p along the effective field (Δω,0, ω₁). And in the transverse plane orthogonal to that vector the magnetization will rotate with the frequency ω_eff. The new rotation axis ω_eff is the eigenvector of the system, which is tilted from the z-axis by $$$\theta$$$=atan(ω₁/Δω). And the relaxation rates are the real parts of the three eigenvalues of the system λ₁=-R_1ρ, λ₂=-R_2ρ -iω_eff, λ₃=-R_2ρ +iω_eff. This means they are a mixture of the old relaxation rates

$$ R_{1\rho}=R_{1a}cos^2\theta+R_{2a}sin^2\theta $$

$$ R_{2\rho}=R_{1a}sin^2\theta+R_{2a}cos^2\theta $$

If the second pool is now considered again, three more eigenvalues would actually appear. However, it can be shown that the contribution to the water signal of these other eigenvalues is rather small and negligible. The strongest change is actually the change of R_1ρ and R_2ρ which are now given by:

$$ R_{1\rho}=R_{1a}cos^2\theta+(R_{2a}+R_{ex})sin^2\theta $$

$$ R_{2\rho}=R_{1a}sin^2\theta+(R_{2a}+R_{ex})cos^2\theta $$

Where R_ex is the exchange-dependent relaxation^4,5 and is part of the smallest eigenvalue of the driven system. We know that R_1ρ is the smallest eigenvalue, so if we calculate again the smallest eigenvalue of the driven system, R_ex can be determined and the problem is solved. It can be shown that instead of solving the whole eigenvalue problem the smallest eigenvalue can be derived by the formula $$$ \lambda_1=-\frac{c_0}{c_1} $$$ where c₀ and c₁ are the first two coefficients of the characteristic polynomial⁴.

This calculus yields R_ex in a general form⁵:

$$ R_{ex}'=sin^2\theta \cdot R_{ex}=f_bk_b\underbrace{\frac{\delta\omega_b^2}{\omega_1^2+\Delta\omega^2}}_{a-peak}\underbrace{\frac{\omega_1^2}{\Gamma^2/4+\Delta\omega_b^2}}_{b-peak}+f_bR_{2b}\frac{\omega_1^2}{\Gamma^2/4+\Delta\omega_b^2}+f_bk_bsin^2\theta\frac{R_{2b}(R_{2b}+k_b)}{\Gamma^2/4+\Delta\omega_b^2} $$

with the width $$$ \Gamma=2\sqrt{\frac{R_{2b}+k_b}{k_b}\omega_1^2+(R_{2b}+k_b)^2} $$$

As R_ex seems to be so fundamental we want to discuss it for 3 experiments: For on-resonant SL it is governed by the “a-peak” and simplifies to the theory of Trott and Palmer^4,5 for on-resonant SL, and shows the typical dispersion with ω₁.

Going from on-resonant spin-lock to a T2 experiment can be done mathematically by the transition ω₁‑>0 which yields directly again the Swift-Connick equation³ (see third eqn above).

Going to the off-resonant case simplifies to a Lorentzian line centered at the CEST resonance;

$$ R_{ex}'=f_bk_b\underbrace{\frac{\omega_1^2}{\omega_1^2+k_b(k_b+R_2b)}}_\alpha\cdot \frac{\Gamma^2/4}{\Gamma^2/4+\Delta\omega_b^2} $$

it directly shows the feature of a selective CEST peak with its amplitude governed by the labeling efficiency α.⁵

Interpretation of data

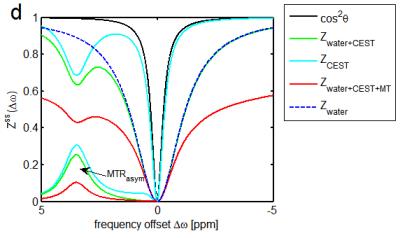
Thus, all mentioned exchange experiments can be described and interpreted by R_ex. For T₂ and T_1ρ on-resonant, the evaluation is clear: one must measure the decay rate R_1ρ. For a CEST experiment, which are often driven to steady-state one has to calculate the z-magnetization after long irradiation that is given by:

$$ Z^{ss}(\Delta\omega)=cos^2\theta\frac{R_{1obs}}{R_{1\rho}(\Delta\omega)} $$

Interestingly, this is the ratio of the free eigenvalue and the driven eigenvalue. Where R_1ρ can actually be extended for multiple pools by

$$ R_{1\rho}= R_{eff}+R_{ex,b}+R_{ex,c}+R_{ex,d}+... $$

As long as the different CEST pools are not exchanging amongst each other. For this also a R_ex,mt was derived that extends the theory for semi-solid MT⁷. Thus by this formula not only the CEST effects can be understood, but also the interplay between multiple-CEST pools, and MT and direct water saturation (spillover effect). Neglecting spillover and MT effects the common CEST formulas e.g. MTR_asym can also be derived. To get R_ex directly an inverse difference can be used. Both methods have their benefits and bootstraps that will be discussed in detail. This calculus can be translated to pulsed CEST by integration of Rex over the pulse shape; also the ability for full quantification by B₁ using the dispersion can be shown for both CEST⁸ and SL⁹.

Acknowledgements

References

1. McConnell, H. M. Reaction Rates by Nuclear Magnetic Resonance. J. Chem. Phys. 28, 430 (1958).

2. Mori, S., Abeygunawardana, C., van Zijl, P. C. & Berg, J. M. Water exchange filter with improved sensitivity (WEX II) to study solvent-exchangeable protons. Application to the consensus zinc finger peptide CP-1. J. Magn. Reson. B 110, 96–101 (1996).

3. Swift, T. J. & Connick, R. E. NMR-Relaxation Mechanisms of O17 in Aqueous Solutions of Paramagnetic Cations and the Lifetime of Water Molecules in the First Coordination Sphere. J. Chem. Phys. 37, 307–320 (1962).

4. Trott, O. & Palmer, Arthur G. Theoretical study of R(1rho) rotating-frame and R2 free-precession relaxation in the presence of n-site chemical exchange. J. Magn. Reson. San Diego Calif 1997 170, 104–112 (2004).

5. Zaiss, M. & Bachert, P. Exchange-dependent relaxation in the rotating frame for slow and intermediate exchange -- modeling off-resonant spin-lock and chemical exchange saturation transfer. NMR Biomed. 26, 507–518 (2013).

6. Zhou, J., Wilson, D. A., Sun, P. Z., Klaus, J. A. & van Zijl, P. C. M. Quantitative description of proton exchange processes between water and endogenous and exogenous agents for WEX, CEST, and APT experiments. Magn. Reson. Med. 51, 945–952 (2004).

7. Zaiss, M. et al. A combined analytical solution for chemical exchange saturation transfer and semi-solid magnetization transfer. NMR Biomed. 28, 217–230 (2015).

8. McMahon, M. T. et al. Quantifying exchange rates in chemical exchange saturation transfer agents using the saturation time and saturation power dependencies of the magnetization transfer effect on the magnetic resonance imaging signal (QUEST and QUESP): Ph calibration for poly-L-lysine and a starburst dendrimer. Magn. Reson. Med. 55, 836–847 (2006).

9. Jin, T., Autio, J., Obata, T. & Kim, S.-G. Spin-locking versus chemical exchange saturation transfer MRI for investigating chemical exchange process between water and labile metabolite protons. Magn. Reson. Med. 65, 1448–1460 (2011).