Synopsis

MR quantitative imaging have been shown to be promising markers for detecting early degeneration and predicting disease progression in musculoskeletal (MSK) imaging due to its relatively independence of scanners/protocols. However, the long acquisition time and associated low resolution quantitative imaging have impeded their wide applications in clinical trials and practice. Recently compressed sensing and parallel imaging based acceleration methods have shown promise to address these challenges such that the quantitative imaging can be translated into clinical practice. Despite the extensive studies in other applications such as brain imaging, MR quantitative imaging in MSK has been overlooked. This course will teach some acceleration methods combining compressed sensing and parallel imaging and show their applications in MSK imaging.

HIGHLIGHTS

• Fast imaging is needed for translational musculoskeletal quantitative imaging.
• Combination of parallel imaging and compressed sensing promises to significantly reduce the MRI scan time
• This course introduces some acceleration methods and provides a few examples in cartilage imaging

TARGET AUDIENCE

OUTCOME/OBJECTIVES

To understand

• Why we need to accelerate in musculoskeletal imaging
• Methods to accelerate qualitative musculoskeletal imaging
• Methods to accelerate quantitative musculoskeletal imaging
• Future outlook

PURPOSE

METHODS

Acceleration methods for qualitative imaging

Parallel imaging [6-9] and compressed sensing (CS) [10-12] are both fast imaging techniques that could reduce the acquisition time of MR imaging via k-space undersampling below the Nyquist rate. Parallel imaging takes advantage of the availability of multi-channel coils such that the MR images can be reconstructed from multi-channel k-space data sampled below the Nyquist sampling rate. Reconstruction methods such as SENSE [7] and GRAPPA [8] have been used in many clinical routines with 2-3 time accelerations. Theoretically the more the number of channels is, the higher the acceleration can be achieved [9]. However, this maximum usually cannot be achieved due to practical limitations such as noise and imperfect coil geometry. Compressed sensing is based on a new theoretical framework for data sampling and signal recovery. Initially investigated in [12], compressed sensing has been studied extensively in accelerating MRI. In compressed sensing MRI, we deal with the problem of recovering a signal (or image) from k-space samples far fewer than what the Shannon sampling theory requires, and thus the scan time can be reduced. The problem is generally ill-posed, suggesting there is no unique solution. Compressed sensing utilizes the property that the signal is sparse (or transform sparse) to allow exact recovery of the signal from reduced samples. Reconstruction of the signal usually requires solving an optimization problem enforcing both sparsity and data consistency. Several methods have been developed to integrate parallel imaging and compressed sensing for morphological imaging [13-17]. Recent Sparse BLind Iterative Parallel (BLIP) [15], simultaneous autocalibrating and k-space estimation (SAKE) [17], and Multi-chAnneL Blind dE-Convolution (MALBEC) [18] methods have shown to reconstruct high quality images at high acceleration factors, among then MALBEC has the lowest computational complexity which makes online 3D reconstruction possible. Here we will focus on MALBEC.

In 3D morphological imaging with multi-channel acquisition, we acquire 3D k-space data that are 2D undersampled along phase and slice encoding directions. Unlike most compressed-sensing methods where the reconstruction is performed in image domain with the sparsity constraints, MALBEC formulates the reconstruction problem as to recover the unacquired data in k-space from all channels using blind deconvolution. Specifically, the k-space data from L channels are the convolution between the k-space data of the desired unknown image and the k-space of the coil sensitivities for each of the L different channels. We wish to recover the full k-space data from the undersampled k-space without knowledge about the coil sensitivities. Apparently, the problem is ill-posed with non-unique solutions. Since the coil sensitivities vary smoothly in image domain, to solve the ill-posed problem, we first assume their k-space values to have significant values only within a small window of size M by N, which is much smaller than the size of the image. We then decouple the problem into solving two linear problems alternately and iteratively: s step - solving for the image in k-space with sensitivities fixed, and h step - solving for the support-limited sensitivities in k-space with the image fixed. The problem is initialized with the k-space coil sensitivities estimated from the low resolution images. The method is highly efficient in computation and has no parameters to tune, so it is suitable for online reconstruction. After convergence, we obtain the desired image.

Acceleration methods for quantitative imaging

For accelerating quantitative imaging, several compressed sensing techniques have been developed [19-28]. These techniques exploit different constraints on the series of parameter weighted images, such as sparseness in the principal component analysis domain [20,21] or in a learned dictionary [22], low rankness [23,24], or the parametric model [25-28]. To take advantage of the availability of large array coils in these method, parallel imaging is usually integrated in these techniques in a straightforward way by incorporating sensitivity encoding in the imaging equation, where the sensitivity maps are poorly estimated. Here we will focus on a method that improves the sensitivity accuracy by iteratively updating the sensitivity functions LAISD JSENSE [29].

In accelerated quantitative (e.g., T1ρ or T2) imaging, we need to reconstruct images from undersampled acquisition at different time points (e.g., spin-lock (TSLs) or echo times (TEs)). The LAISD JSENSE method reconstructs the images at all times simultaneously, integrating compressed sensing and parallel imaging. The method assumes the image series to be sparse in the principal component space along time. The image series, defined as $$$S$$$, is reconstructed by $$\min_{S, H_c}\|PS\|_1 \quad s.t. \quad \sum_{c,t}\|y_c-\Omega F(S_t \cdot H_c)\|^2_2<\epsilon.$$ where P represents the principal component analysis projection matrix that maps $$$S$$$ from the original space to the principal component space, $$$y_c$$$ represents the acquired k-space data from the $$$c$$$th channel, $$$F$$$ represents the spatial Fourier transform, and $$$\cdot$$$ denotes the pixel-wise multiplication from the unknown coil sensitivity modulation. Similar alternating optimization approach is taken to solve the problem iteratively with S step and H step. The S step can be solved with k-t ISD [30] (or any compressed sensing approach) with known sensitivities, while the H step is to solve a linear equation. For quantitative imaging of tiny structures such as cartilage, locally adaptive thresholding (LAISD) should be use for k-t ISD to improve the accuracy in the S step.

EXAMPLES

Accelerated Cartilage T1ρ Imaging

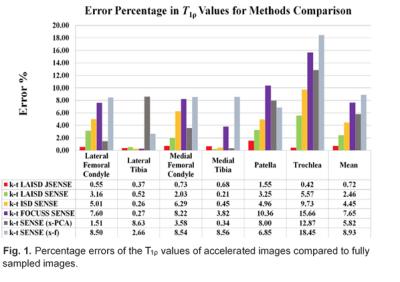
Here we provide an example for accelerated quantitative imaging using Cartilage T1ρ Imaging. We compared in Fig. 1 the T1ρ quantification errors from six different acceleration methods: k-t LAISD JSENSE [29], k-t LAISD [29], k-t ISD [30], k-t FOCUSS [20], and k-t SENSE [31] in x-f domain and x-PCA domain, where conventional SENSE was used for coil sensitivity estimation and the acceleration factor (AF) was 4. Cartilage was segmented semi-automatically into six compartments (LFC: lateral femoral condyle; LT: lateral tibia; MFC: medial femoral condyle; MT: medial tibia; Pat: patella; T: trochlea) based on edge detection and Bezier splines [32]. Figure 1 shows the T1ρ errors in all compartments from six knees are below 1% for k-t KAISD JSENSE. Figure 2 A-D show example fully-sampled and undersampled T1ρ and T2 maps . It demonstrated the feasibility of accelerating quantitative cartilage imaging.

Accelerated 3D FSE (CUBE) Imaging

For 3D CUBE image, we used MalBEC to reconstruct the image from undersampled k-space data, where variable density (VD) random Poisson disk undersampling [33] was employed along the both phase and slice encoding directions. Fig. 2E and 3F demonstrate example CUBE images with prospective 2D undersampling (along both phase and slice directions, AF=8). It shows MalBEC method is able to accelerate 3D CUBE by factors up to 8 without degrading the image quality. In summary, these examples demonstrated the feasibility of accelerating cartilage T1ρ, T2, and morphologic imaging (3D FSE, CUBE) using advanced algorithm combining compressed sensing and parallel imaging.

DISCUSSION

CONCLUSION

Acknowledgements

References

1. Li X, Kuo D, Theologis A, Carballido-Gamio J, Stehling C, Link TM, Ma CB, Majumdar S. Cartilage in anterior cruciate ligament reconstructed knees: MR imaging T1ρ and T2-initial experience with 1-year follow-up. Radiology 2011;258:505–514.
2. Li X, Pai A, Blumenkrantz G, Carballido-Gamio J, Link T, Ma B, Ries M, Majumdar S. Spatial distribution and relationship of T1ρ and T2 relaxation times in knee cartilage with osteoarthritis. Magn Reson Med 2009;61:1310–1318.
3. Keenan KE, Besier TF, Pauly JM, Han E, Rosenberg J, Smith RL, Delp SL, Beaupre GS, Gold GE. Prediction of glycosaminoglycan content in human cartilage by age, T1ρ and T2 MRI. Osteoarthritis Cartilage 2011;19:171–179.
4. Taylor C, Carballido-Gamio J, Majumdar S, Li X. Comparison of quantitative imaging of cartilage for osteoarthritis: T2, T1ρ, dGEMRIC and contrast-enhanced computed tomography. Magn Reson Imaging 2009;27:779–784.
5. Li X, Benjamin Ma C, Link TM, Castillo D-D, Blumenkrantz G, Lozano J, Carballido-Gamio J, Ries M, Majumdar S. In vivo T1ρ and T2 mapping of articular cartilage in osteoarthritis of the knee using 3 Tesla MRI. Osteoarthritis and cartilage 2007;15:789–797.
6. Sodickson DK, Manning WJ. Simultaneous acquisition of spatial harmonics (SMASH): Fast imaging with radiofrequency coil arrays. Magn Reson Med 1997;38:591–603.
7. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med 1999;42:952–962.
8. Griswold MA, Jakob PM, Heidemann RM, Mathias N, Jellus V, Wang J, Kiefer B, and Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47: 1202–1210.
9. Ying L, Liang ZP. Parallel MRI using phased array coils. IEEE Signal Process. Mag 2010;27: 90–98.
10. Candès EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory 2006;52:489–509.
11. Donoho D. Compressed sensing. IEEE Trans Inf Theory 2006;52:1289–1306.
12. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182–1195.
13. Liu B, Zou YM, Ying L, editors. SparseSENSE: application of compressed sensing in parallel MRI. Information Technology and Applications in Biomedicine, 2008 ITAB 2008 International Conference on; 2008: IEEE.
14. Liang D, Liu B, Wang J, Ying L. Accelerating SENSE using compressed sensing. Magnetic Resonance in Medicine. 2009;62(6):1574-84.
15. She H, Chen RR, Liang D, DiBella EV, Ying L. Sparse BLIP: BLind Iterative Parallel imaging reconstruction using compressed sensing. Magnetic Resonance in Medicine. 2014;71(2):645-60.
16. Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn Reson Med. 2010;64(2):457-71.
17. Shin PJ, Larson PE, Ohliger MA, Elad M, Pauly JM, Vigneron DB, et al. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med. 2014;72(4):959-70.
18. Lyu J, Ying L, editors. Calibration-free parallel imaging using randomly undersampled multichannel blind deconvolution (MALBEC). Annual conference of International Soceity of Magnetic Resonance in Medicine (ISMRM); 2016; Singapore
19. Velikina JV, Alexander AL, Samsonov A. Accelerating MR parameter mapping using sparsity-promoting regularization in parametric dimension. Magnetic Resonance in Medicine. 2013;70(5):1263-73.
20. Feng L, Otazo R, Jung H, Jensen JH, Ye JC, Sodickson DK, et al. Accelerated cardiac T2 mapping using breath-hold multiecho fast spin-echo pulse sequence with k-t FOCUSS. Magnetic Resonance in Medicine. 2011;65(6):1661-9.
21. Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI. T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing. Magnetic Resonance in Medicine. 2012;67(5):1355-66.
22. Doneva M, Börnert P, Eggers H, Stehning C, Sénégas J, Mertins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magnetic Resonance in Medicine. 2010;64(4):1114-20.
23. Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang ZP. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magnetic Resonance in Medicine. 2014.
24. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magnetic Resonance in Medicine. 2015;73(2):655-61.
25. Li W, Griswold M, Yu X. Fast cardiac T1 mapping in mice using a model-based compressed sensing method. Magnetic Resonance in Medicine. 2012;68(4):1127-34.
26. Zhao B, Lam F, Liang Z-P. Model-based MR parameter mapping with sparsity constraints: parameter estimation and performance bounds. Medical Imaging, IEEE Transactions on. 2014;33(9):1832-44.
27. Block KT, Uecker M, Frahm J. Model-based iterative reconstruction for radial fast spin-echo MRI. Medical Imaging, IEEE Transactions on. 2009;28(11):1759-69.
28. Sumpf TJ, Uecker M, Boretius S, Frahm J. Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI. Journal of Magnetic Resonance Imaging. 2011;34(2):420-8.
29. Zhou Y, Pandit P, Pedoia V, Rivoire J, Wang Y, Liang D, et al. Accelerating t cartilage imaging using compressed sensing with iterative locally adapted support detection and JSENSE. Magn Reson Med. 2015; 75(4):1617-29.
30. Liang D, DiBella EV, Chen RR, Ying L. k-t ISD: Dynamic cardiac MR imaging using compressed sensing with iterative support detection. Magnetic Resonance in Medicine. 2012;68(1):41-53.
31. Tsao J, Boesiger P, Pruessmann KP. k-t BLAST and k-t SENSE: Dynamic MRI with high frame rate exploiting spatiotemporal correlations. Magn Reson Med 2003;50:1031–1042.
32. Carballido-Gamio J, Bauer JS, R. S, Lee KY, Krause S, Link TM, Majumdar S. Inter-subject comparison of MRI knee cartilage thickness. Med Image Anal 2008;12:120–135.
33. Nayak KS, Nishimura DG. Randomized trajectories for reduced aliasing artifact. Proceedings of the 6th Annual Meeting of ISMRM, Sydney, Australia; 1998
34. Dan Ma, Vikas Gulani, Nicole Seiberlich, Kecheng Liu, Jeffrey L. Sunshine, Jeffrey L. Duerk, Mark A. Griswold. Magnetic resonance fingerprinting. Nature 495: 187–192