Cartesian & Non-Cartesian Sampling Schemes - Advantages & Disadvantages
1Department of Biomedical Engineering, University of Virginia, Charlottesville, VA, United States
Synopsis
This educational talk will cover the advantages and disadvantages of Cartesian and non-Cartesian sampling techniques. Cartesian, radial, and spiral k-space scanning methods will be compared with respect to scan efficiency, hardware considerations, off-resonance effects, motion sensitivity, and scan acceleration.
Highlights
· Cartesian sampling is a robust and established method with many practical advantages.
· Non-Cartesian sampling methods also have a number of advantages and methods have been developed for mitigating their disadvantages.
Target Audience
Research scientists, engineers, and clinicians interested in a practical discussion of the advantages and disadvantages of radial and spiral k-space scanning methods relative to conventional Cartesian sampling.Outcome/Objectives
To understand the advantages and disadvantages of Cartesian, radial, and spiral k-space scanning methods with respect to scanning efficiency, hardware considerations, off-resonance effects, motion sensitivity, undersampling, and scan acceleration methods.Overview
Conventional Cartesian k-space scanning, or spin warp imaging [1], is a fundamental method that has played an essential role in the clinical and scientific success of MRI. It is a robust technique that has been successfully used with a wide variety of hardware and is the primary method used clinically. However, there are an infinite number of ways to scan k-space, and non-Cartesian methods have been studied for many years, dating back to Lauterbur’s original NMR imaging paper [2]. Researchers have addressed many of the practical methodological concerns with non-Cartesian methods and have explored potential applications of these methods. This talk will compare spin warp to two widely studied non-Cartesian methods: radial and spiral scanning. Are these methods ready for broader clinical use? This talk will explore the tradeoffs underlying this question.Sampling Considerations
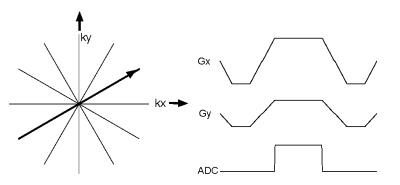
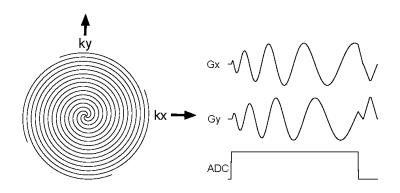
Figure 1 shows a typical radial k-space trajectory and the corresponding readout gradients. Radial readout gradients are similar to Cartesian readout gradients, but they are rotated to scan 2D k-space rather than phase encoded. The result is that the underlying field of view (FOV) is circular rather than rectangular. Figure 2 shows an interleaved spiral trajectory and corresponding readout gradients, which are effectively rotated during the course of each readout. The underlying spiral FOV is also circular, though the point spread function is different from that of a radial trajectory. Spiral scans can cover all of k-space in a single shot, but can be used with a larger number of interleaves for high resolution scans. The spirals shown in Fig. 2 are constant density (Archimedean) spirals, but spirals can also be designed to have a variable sampling density as a function of radius. A key disadvantage of radial and spiral sampling is that there is no dedicated readout direction, which means that spatial aliasing along one direction cannot be eliminated using the temporal anti-aliasing filter. Thus, the prescribed non-Cartesian FOV must be large enough to prevent aliasing in all directions, or else other techniques must be used to prevent aliasing.Scan Efficiency
Two important considerations of efficiency are the minimum scan time and the SNR efficiency of the scan. Cartesian scans require a number of readouts equal to the number of resolution elements in the phase encoding direction. The scan time is often reduced using partial Fourier methods or by prescribing a rectangular FOV. The uniform Cartesian sampling pattern yields optimal SNR, but the relatively large number of readouts leads significant overhead for the RF pulses. A fully-sampled radial scan requires more readouts than a Cartesian scan and the SNR efficiency is lower, because of the significant sampling density variation and thus unequal weighting of the noise. A spiral scan requires approximately 5-10 times fewer readouts than a Cartesian scan of similar resolution and FOV. The SNR efficiency of a constant-density spiral scan is relatively high, although slew rate limitations and the repeated sampling of the center of k-space lead to somewhat unequal weighting of the noise. So, for fully-sampled scans, the scan efficiency of spirals is the highest overall, followed by Cartesian and then by radial [3]. However, undersampled radial scans can be very fast when combined with advanced image reconstruction techniques.
Hardware Considerations
Cartesian scanning is particularly robust in the presence of scanner hardware imperfections, including eddy currents, timing delays, and filter anisotropy. However, modern scanners are capable of producing high-quality radial and spiral images with appropriate calibration and image reconstruction procedures. With radial scanning, it is important to account for anisotropic gradient delays [4]. For spiral scanning, it is typically desirable to perform a one-time calibration for gradient delays and eddy currents [5-7]. Overall, while robustness to hardware imperfections remains an advantage of Cartesian scans, a properly calibrated non-Cartesian scan has minimal image quality degradation with modern hardware.Main Field Inhomogeneity
The primary effect of typical main field inhomogeneity on a Cartesian scan is a relatively minor geometric distortion. The effect on a radial scan is a minor amount of image blur. The effect on a spiral scan can be significant image blur if not corrected. This effect can be mitigated by using a large number of interleaves, but this reduces the scan time advantage of spiral scans. The blur can be largely removed in image reconstruction, using one of a variety of methods, including methods that derive a field map automatically [8]. However, this is still a disadvantage of spirals relative to Cartesian and radial.Motion
Cartesian scans can suffer from image artifacts and ghosting in the presence of cardiac, respiratory, and patient motion. Radial and spiral scanning have a clear advantage in this area, primarily because of the repetitive sampling of the high-energy center of k-space. This talk will give an overview of how this motion robustness and image acceleration techniques enabled by non-Cartesian sampling can improve cardiac, abdominal, and neuro imaging.
Acknowledgements
Funding support from NIH R21 EB022309 and collaborations with John Mugler and Josef Pfeuffer.References
1. Edelstein WA, Hutchison JM, Johnson G, Redpath T. Spin warp NMR imaging and applications to human whole-body imaging. Phys Med Biol. 1980 Jul;25(4):751-6.
2. Lauterbur PC. Image formation by induced local interactions: examples employing nuclear magnetic resonance. Nature 242, 190–191 (1973).
3. Feng X, Salerno M, Kramer CM, Meyer CH. Non-Cartesian balanced steady-state free precession pulse sequences for real-time cardiac MRI. Magn Reson Med. 2016 Apr;75(4):1546-55.
4. Peters DC, Derbyshire JA, McVeigh ER. Centering the projection reconstruction trajectory: reducing gradient delay errors. Magn Reson Med. 2003 Jul;50(1):1-6.
5. Tan H, Meyer CH. Estimation of k-space trajectories in spiral MRI. Magn Reson Med. 2009 Jun;61(6):1396-404.
6. Addy NO, Wu HH, Nishimura DG. Simple method for MR gradient system characterization and k-space trajectory estimation. Magn Reson Med. 2012 Jul;68(1):120-9.
7. Campbell-Washburn AE, Xue H, Lederman RJ, Faranesh AZ, Hansen MS. Real-time distortion correction of spiral and echo planar images using the gradient system impulse response function. Magn Reson Med. 2016 Jun;75(6):2278-85.
8. Chen W, Sica CT, Meyer CH. Fast conjugate phase image reconstruction based on a Chebyshev approximation to correct for B0 field inhomogeneity and concomitant gradients. Magn Reson Med. 2008 Nov;60(5):1104-11.