Synopsis

The pre-scan adjustments, while nearly invisible to many practitioners, are very important for the successful acquisition of many spectroscopic and imaging sequences. In this talk, approaches and constructs specific to B0 and B1 optimization are discussed with examples of methods and results.

B0 and B1 performance are commonly among the most critical factors needed in the acquisition of MR spectroscopic data. Problems with either of these are commonly a key limitation for increasingly complex acquisitions; e.g., multiple spin echo sequences that are played out in the context of inhomogeneous B1 fields will suffer from substantially smaller volumes in comparison to more homogeneous B1 fields, by virtue of the spatial sin2 (B1τp) dependence arising from each additional spin echo. Problems resulting from less than excellent B0 homogeneity are readily identified by signal distortion and dropout from echo-planar imaging, and for spectroscopy, can make water suppression difficult and spectra un-interpretable. Ironically, under many current MR conditions, optimization of these critical parameters are wholly invisible to the user, only appearing as a sub-text of “adjust volume” or “RF adjustment”. In this talk we discuss some key approaches for B0 and B1 optimization in preparation for a spectroscopic study.

B0 shimming

The presence of varying paramagnetic or diamagnetic tissue susceptibilities and interfaces within the magnet bore results in B0 field distortion. With (passive and) active shim devices, the goal of the B0 shimming is to compensate for such field distortion. Starting with a homogeneous sample, the most commonly used analytic approach to describe (and compensate) the magnetic fields are spherical harmonic functions. Carrying DC current, appropriately designed shim coils generate such spherical harmonic terms. Thus the process of shimming determines how much current to allocate to each shim coil in order to optimize the resulting B0 homogeneity.

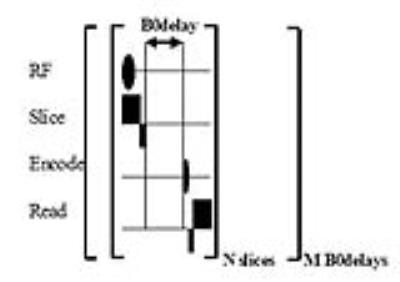
There are a number of methods available to measure the field with the majority being based on an incremented delay gradient echo. This phase mapping approach was used initially with columns (Gruetter 1992; Shen 1999) but is more completely performed with maps (Fig. 1).

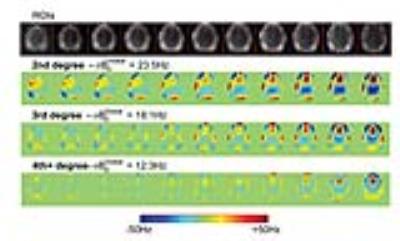
In this approach, individual excitations are taken of progressively longer evolutions of the B0 encoding delay, e.g., 1,2, 4 and 8ms. With this multiple evolution approach, the B0 map is calculated with the bandwidth of the shortest encoding time but with the resolution of the longest encoding time, ­­±500Hz for 1ms encoding time ­at 0.3Hz/degree (8ms). Applying this approach in the human head readily shows the anticipated areas of field inhomogeneity emanate from the sinuses and bony interfaces, but also that more complex shim geometries are needed to achieve homogeneity in regions of high inhomogeneity (Fig. 2). The implementation of a 1st-4th high degree shim insert achieves a 50% reduction in overall field homogeneity. As seen in Fig. 2 in the high brain slices, the correction of additional an nth shim degree reveals the next higher n+1th residual inhomogeneity.

With such maps, the notions of global B0 inhomogeneity variance (σB0global as measured over the entire sample) and local B0 inhomogeneity variance (σB0local, measured over a 1cc voxel) also become grossly evident, i.e., the mean variance of B0 homogeneity over the entire sample versus a small area are different parameters, although both impact the performance of spectroscopic studies. For spectroscopic imaging where large volume B0 homogeneity is important, it is worth noting that the σB0global bears on the overall water suppression adequacy of the study (given that there is only one system frequency f0 from which the entire study is acquired) while σB0local clearly relates to the linewidth of individual spectra.

B1 optimization and shimming

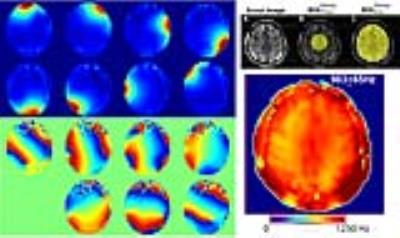
It is well known that due to RF-tissue interactions, the shorter wavelengths at ultra high field result in significant B1 inhomogeneity as produced by volume head coils (Fig. 3), characterized by a hot center region, and not reparable by B1 calibration.

Thus at ultra-high field and as discussed by many, parallel transmission or multiple RF coils enable more control over the B1 distribution, and with RF shimming, can provide excellent B1 amplitude and homogeneity over large brain volumes. As realized with the inductively decoupled transceiver (Fig. 4, showing a double row 16 channel transceiver), pairs of individual coil elements are driven by independent RF amplifiers. In this case, RF optimization is achieved through the RF shimming process, performed with B1+ amplitude and phase maps that characterize each of the individual coil pairs. The amplitudes and phases of the RF generated by the coils can be measured by many different methods (e.g., Sackolick 2010; Insko and Bolinger 1993; Pan 1998).

Recognizing that the individual coils of the transceiver will exhibit constructive and destructive summation over the object (Fig. 5), RF shimming targets a coherent phase region in the center, approximately generating the circularly polarized phase shift of 360/n degrees over the n-circumferential coils. With the phases thus determined from a center region of interest, the amplitudes of individual drives are optimized to achieve the desired B1. It should be noted that in the center where the phase variation is slow for all coils (and all coils contribute), the summation of B1 is largely constructive and highly efficient, while at the more proximal edges the phase variation is high (dominated by a small number of coils), the summation of B1 includes some destructive interference and is thus less efficient. In such a coil design however, the regions of destructive interference and low efficiency are constrained to edge regions and thus the entire transceiver remains highly efficient.

In total, the integrated performances of such “Pre-Scan” adjustments are major factors in the subsequent success of the spectroscopic studies. While individual acquisitions can be made more or less robust to individual aspects of B0 or B1, there can be significant play-off between them such that overall, it pays to make sure that both the B0 and B1 are optimal for the eventual goals.

Acknowledgements

References

Avdievich NI, Pan JW, Baehring JM, Spencer DD, Hetherington HP. Short echo spectroscopic imaging of the human brain at 7T using transceiver arrays. Magn Reson Med. 2009;62(1):17-25.

Gruetter R, Boesch C. Fast not interative shimming of spatially localized signals. In vivo analysis of the magnetic field long axis. J Magn Res 1992:96:323-334.

Hetherington H, Chu WJ, Gonen O, Pan JW. Robust fully automated shiming of the human brain for high field 1H spectroscopic imaging. 2006:56:26-33.

Pan JW1, Twieg DB, Hetherington HP. Quantitative spectroscopic imaging of the human brain. Magn Reson Med. 1998 Sep;40(3):363-9.

Pan JW, Lo KM, Hetherington HP. Role of very high order and degree Bo shimming for spectroscopic imaging of the human brain at 7T. Magn Res Med 2012:68:1007-1017.

Shen J, Rothman D, Hetherington H, Pan J. Linear projection method for automatic slice shimming. Magn Res Med 1999:42:1082-1088.

Sacolick LI, Wiesinger F, Hancu I, Vogel MW. B1 mapping by Bloch-Siegert shift. Magn Res Med 2010;63(5):1315-22.

Yarnykh VL. Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn Res Med 2007; 57: 192–200.

Zhang X, Schmitter S, Van de Moortele PF, Liu J, He B. From complex B(1) mapping to local SAR estimation for human brain MR imaging using multi-channel transceiver coil at 7T. IEEE Trans Med Imaging. 2013 Jun;32(6):1058-67.