Diffusion Weighted Imaging & Applications
1Institute for Systems and Robotics / Department of Bioengineering, Instituto Superior Técnico, University of Lisbon, Lisbon, Portugal
Synopsis
Diffusion-weighted imaging (DWI) makes use of molecular water motion to probe tissue microstructure. This lecture will focus on the basic principles of DWI acquisition. After introducing the most commonly used diffusion modules, the main acquisition challenges will be discussed. Typical acquisition approaches will be presented, including single-shot and multi-shot sequences. Examples of frequent DWI image artefacts will be shown, and some of the approaches available for minimizing or correcting for their effect will be presented. The main applications of DWI to brain and body imaging will also be presented, focusing on stroke and lesion characterization.
What is diffusion?
The phenomenon of diffusion was first described by Robert Brown in the 19th century, after observing particles of pollen moving in a water solution [1]. This random translational motion arises from the thermal energy carried by particles. As demonstrated by Einstein [2], in the absence of obstacles (free diffusion), the mean square displacement is proportional to the diffusion time τ and the diffusion coefficient D of the medium:
$$⟨r^2⟩=6Dτ$$
where r represents the three-dimensional displacement during the period τ. To give an idea, since the diffusion coefficient of water molecules at room temperature is 2.3×10−3 mm2/s [3], the root mean square displacement for a diffusion time of 10 millisecond (on the order of that used in MR experiments) is on the order of 10μm. This length is much smaller than the typical size of imaging voxels (about a millimeter), and comparable to cellular dimensions. The reason why diffusion-weighted imaging (DWI) is such a powerful tool is that it allows us to use water molecules to probe tissue structures much smaller than the achievable voxel sizes.
Measuring diffusion with MR
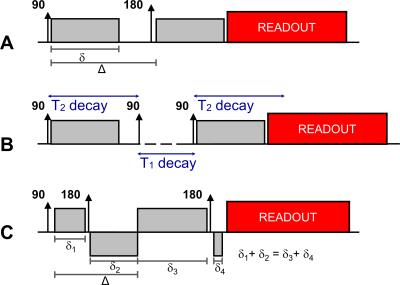
Hahn first noted the effects of diffusion on MR signals in 1950 [4]. To describe them, in 1956 Torrey added an extra term to the Bloch Equations, creating the well-known Bloch-Torrey equation [5]. Stejskal and Tanner were the first to propose the use of a pulsed-gradient spin echo sequence (PGSE) for diffusion measurements in 1965 [6]. The Stejskal-Tanner diffusion module consists of a pair of gradients with the same amplitude G and duration δ with an 180° RF pulse applied in between – Figure 1A. The interval between application of the two diffusion gradients is often labelled as Δ. By solving the Bloch-Torrey equation it is possible to demonstrate that the MR signal will be multiplied by an additional diffusion term: $$S(b)=S_0.exp(-bD)$$
where S0 is the T2-weighted signal measured at the echo time TE in the absence of diffusion gradients, and b describes the sequence's sensitivity to diffusion which can be calculated from:
$$b=\gamma^2\int_{0}^{TE} (\int_{0}^{t'}G(t')dt')^2dt$$
which in the case of the PGSE module results in:
$$b=(\gamma.Gδ)^2(Δ-δ/3)$$
Note that the MR signal is only sensitive to diffusion occurring along the direction of the diffusion gradient as shown in Figure 2.
One of the main challenges of diffusion-weighted (DW) imaging results from the fact that a higher diffusion contrast implies stronger signal attenuation. Additionally, as achieving a higher b-value typically requires longer diffusion gradients, longer echo times are needed when using the PGSE module. DW images thus typically suffer from a low signal-to-noise ratio and this is further aggravated with increasing b-values. An alternative to PGSE is to use a stimulated-echo diffusion-sensitisation module (Figure 1B). By storing the magnetization in the longitudinal axis after applying the first diffusion gradient, it is possible to increase the b-value by increasing the time interval between the two gradients instead of prolonging them, thus limiting T2-decay. The disadvantage of this approach is the 50% signal penalty inherently associated to stimulated echoes.
Diffusion Imaging Sequences
Given that the DW signal needs to detect very minute molecular motion, it is extremely sensitive also to any other type of motion. Subject motion during the PGSE module affects the phase of the transverse magnetization, resulting in a spatially varying phase pattern [7]. By sampling k-space following a single excitation, inconsistencies between k-space segments can be avoided. Single-shot Echo-Planar Imaging (EPI) is therefore still the sequence most commonly used to acquire DW images [8]. An additional advantage of single-shot EPI is that it enables the acquisition of several images, with varying b-values and/or diffusion directions, within reasonable scanning times.
On the other hand, the T2* signal decay occurring during the long EPI readout (of the order of 100 ms) limits the achievable image resolution. To increase it further, multi-shot approaches can be used, but require calibration of the motion-induced phase patterns. The use of navigator echoes was initially proposed [9,10] but recently a promising alternative based on parallel imaging has been suggested [11].
Due to its long readout window, single-shot EPI is also extremely sensitive to eddy currents. As diffusion-sensitisation requires high amplitude gradients applied for a long period, eddy current fields are produced which may linger during the readout period and result in geometric image distortions [12]. The doubly-refocused module (Figure 1C) is often used as an alternative to the PGSE module since by adjusting the duration of the diffusion gradients it is possible to null dominant eddy current fields [13].
Applications of DWI
The first application of DWI, in which it continues to have a significant impact, was in stroke imaging. Moseley et al. demonstrated that diffusivity is significantly decreased minutes after an infarct, with the affected areas appearing brighter in DW images with no visible changes in conventional images [14]. Since it allows probing tissue microstructure, DWI is often used for lesion characterization both in the brain (e.g. in neurodegenerative diseases [15] and tumours [16]) and in other parts of the body. A recent review of DWI body imaging can be found in [17].Acknowledgements
Fundação Luso-Americana para o Desenvolvimento (FLAD) and Portuguese Foundation for Science and Technology (UID/EEA/50009/2013).References
[1] R Brown. A brief account of microscopical observations made in the months of june, july and august of 1827 on the particles contained in the pollen of plants and on the general existence of active molecules in organic and inorganic bodies. Phylosophical Magazine, 4, 161–173. (1828).
[2] A Einstein. Investigations on the theory of the Brownian movement, collection papers translated from german, edited by R Furth and AD Cowper, Dover, New York, (1956).
[3] DL Thomas, MF Lythgoe, GS Pell, F Calamante, and RJ Ordidge. The measurement of diffusion and perfusion in biological systems using magnetic resonance imaging. Physics in Medicine and Biology, 45, R97–138. (2000).
[4] E L Hahn. Spin echoes. Physical Review, 80:580–594 (1950).
[5] HC Torrey. Bloch equations with diffusion terms. Physical Review, 104, 563–565. (1965).
[6] EO Stejskal and JE Tanner. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. Journal of Chemical Physics, 42, 288–292. (1965).
[7] AW Anderson and JC Gore. Analysis and correction of motion artifacts in diffusion weighted imaging. Magnetic Resonance in Medicine, 32, 379–87 (1994).
[8] R Turner, D Le Bihan, J Maier, R Vavrek, LK Hedges, and J Pekar. Echo-planar imaging of intravoxel incoherent motion. Radiology, 177, 407–14 (1990).
[9] K Butts, J Pauly, A de Crespigny, and M Moseley. Isotropic diffusion-weighted and spiral-navigated interleaved EPI for routine imaging of acute stroke. Magnetic Resonance in Medicine, 38, 741–9 (1997).
[10] KL Miller and JM Pauly. Nonlinear phase correction for navigated diffusion imaging. Magnetic Resonance in Medicine, 50, 343–53 (2003).
[11] NK Chen, A Guidon, HC Chang, AW Song. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage, 15,:41-7 (2013).
[12] P Jezzard, AS Barnett, and C Pierpaoli. Characterization of and correction for eddy current artifacts in echo planar diffusion imaging. Magnetic Resonance in Medicine, 39, 801–12. (1998).
[13] TG Reese, O Heid, RM Weisskoff, and VJ Wedeen. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magnetic Resonance in Medicine, 49, 177–82. (2003).
[14] ME Moseley, Y Cohen, J Mintorovitch, L Chileuitt, H Shimizu, J Kucharczyk, M F Wendland, and P R Weinstein. Early detection of regional cerebral ischemia in cats: comparison of diffusion- and T2-weighted MRI and spectroscopy. Magnetic Resonance in Medicine, 14, 330–46. (1990).
[15] J Goveas J, L O'Dwyer, M Mascalchi, M Cosottini, S Diciotti, S De Santis, L Passamonti, C Tessa, N Toschi , M Giannell. Diffusion-MRI in neurodegenerative disorders. Magn Reson Imaging. 33:853-76. (2015).
[16] SE Maier, Y Sun, RV Mulkern. Diffusion Imaging of Brain Tumors. NMR in biomedicine 23:849–864 (2010)
[17] B Taouli, AJ Beer, T Chenevert, D Collins, C Lehman, C Matos, AR Padhani, AB Rosenkrantz, A Shukla-Dave, E Sigmund, L Tanenbaum, H Thoeny, I Thomassin-Naggara, S Barbieri, I Corcuera-Solano, M Orton M, SC Partridge, DM Koh. Diffusion-weighted imaging outside the brain: Consensus statement from an ISMRM-sponsored workshop. J Magn Reson Imaging. 44(3):521-40. (2016).