Artifact to Information using Structured Low Rank Matrix Completion
1Dept. Bio/Brain Engineering, KAIST, Daejeon, Korea, Republic of
Synopsis
MRI artifacts arise from various sources, including instability of an MR system, patient movement, inhomogeneities of gradient fields, etc. Such MRI artifacts are generally considered as irreversible so that additional artifact-free scan or navigator scan is required. To overcome these limitations, this paper discusses the physical origin of various MR artifacts and novel compressed sensing-based approaches for removing these MRI artifacts.
Purpose
Many types of MR image artifacts are generated from outliers in the k-space measurements. For example, herringbone artifacts (also called as crisscross artifact) are scattered throughout the image in a single slice or multiple slices, rendering the images unusable. The main origin of this artifact consists of electromagnetic spikes through gradient coils or fluctuating power supply, which generally leads to outliers in the k-space measurement domain. Zipper artifacts are similarly generated due to the insertion of external RF noises at specific frequency. Because zipper artifacts occur through consistent RF noises during data acquisition, RF noise appears as line structures in the image domain that is different from herringbone artifacts. On the other hand, motion artifacts are also often observed when a subject moves during scanning. Due to the motion during k-space sampling, some of the k-space data lose their integrity from the neighborhood k-space data, which can be also considered as outliers.On the other hand, MR measurements from an EPI sequence produce Nyquist ghost artifacts derived from inconsistencies between odd and even echoes.
To remove these artifacts, several reconstruction algorithms have been proposed. In this course, we review the classical approaches as well as advanced algorithms using structured matrix completion.
Theory
Recently, the annihilating filter based low-rank Hankel matrix (ALOHA) approach has been proposed for compressed sensing and parallel MRI. ALOHA uses the duality between the low-rankness of weighted Hankel structured matrix and the sparsity of signal in a transform domain in order to unify parallel MRI and CS-MRI. Specifically, ALOHA is based on a novel observation that the transform domain sparsity in the image space implies the low rank of weighted Hankel matrix in the reciprocal space. This converts pMRI and CS-MRI to a k-space interpolation problem using a structured matrix completion after a suitable weighting in the k-space data. Using this structured low rank properties, two types of artifact correction methods can be derived.
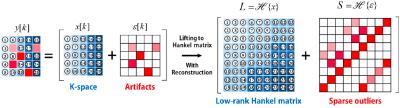
First, we can implement a sparse and low rank decomposition algorithm for the removal of MRI artifacts originating from the k-space outliers. By using the annihilating filter-based low rank Hankel matrix (ALOHA) approach, we can show that many MR artifacts can be represented as sparse outliers, while k-space data from the underlying artifact-free image can be decomposed as a low-rank component of a Hankel matrix constructed from the k-space measurements. Therefore, by applying sparse and low-rank decomposition approach as in the robust principal component analysis (RPCA), we can decompose the artifact signals from the underlying artifact free image.
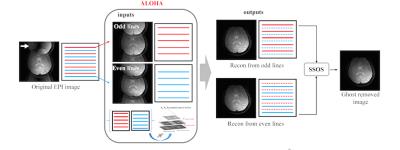
Second, for the EPI ghost artifact correction, a ghost correction problem can be reformulated as a k-space data interpolation problem for even and odd phase encoding lines to exploit that differential k-space data between the even and odd echoes is a Fourier transform of an underlying sparse image. Accordingly, we can construct a Hankel structured matrix whose missing data can be recovered with low rank Hankel structured matrix completion.
Methods
Recently, ALOHA was proposed as a powerful tool for compressed sensing MRI and image processing [1-5]. More specifically, if the signal x(t) is sparse, then there exists an annihilating function h such that
$$x(t) h(t) = 0 \overset{FT}{\longleftrightarrow} \hat{x}(k) * \hat{h}(k) = 0 \quad\quad\quad (1) $$
where $$$\hat{x}(k) $$$ denotes the Fourier transform of $$$x(t)$$$. In particular, if $$$x(t)$$$ is represented as sum of Diracs, then becomes a finite impulse response filter $$$\hat{h}(k) $$$. Thus, Eq. (1) can be rewritten as matrix-vector form
$$\mathcal{H}\left(\hat{x}\right)\bar{h} = 0 \quad\quad\quad (2)$$
where $$$\mathcal{H}$$$ is Hankel matrix and $$$\bar{h}$$$ is the reverse ordered, vectorized annihilating filter. As mentioned before, some artifacts in MRI can be modeled as k-space sparse outliers. Accordingly, MRI k-space measurements can be modeled as
$$\hat y(k) = \hat x(k) + \hat \epsilon(k) \quad\quad\quad (3) $$
where $$$\hat x(k)$$$ is a k-space data of artifact-free image and $$$\hat\epsilon(k)$$$ is sparse k-space outlier. In Eq. (3), if the underlying image is sparse, the first term has an annihilation property as reviewed in Eq. (1)-(2), whereas the second term is irrelevant with annihilation property because of irregular structures. This implies that we can use the annihilation property as a differentiation tool between MRI artifacts and true MR images. Note that lifted Hankel matrix from sparse components is still sparse as shown in Fig. 1. Therefore, Eq. (3) becomes a structure for sparse + low-rank Hankel matrix. Because RPCA (robust principal component analysis) has been extensively investigated for sparse + low-rank decomposition, we employ the main idea of RPCA to decompose ALOHA matrix for a removal of MRI artifact.
On the other hand, to investigate EPI ghost correction, we need to discuss EPI physics. Recall that an EPI sequence of each n-th line can be expressed as
$$S_n(k_x,k_y)=\int\int m(x,y)e^{j2\pi \left[ \Delta f(x,y) \left( TE+ (n-N/2)ESP \right) \right]} e^{j2\pi \left[ \Delta f(x,y) (-1)^n\left( \frac{k_x}{\gamma G_x} \right) +k_x x+k_y y \right]}dxdy$$
where m
is image intensity and Δf is frequency off-set due to the field
inhomogeneity. TE is the echo time, and ESP denotes the echo spacing. N is the
total number of echoes. From this equation, the virtual k-space data from even
and odd can be defined, and the real EPI measurements can be identified as
their ½ -subsampled data. Then, the difference between virtual even and odd k-space data can be represented by
$$S_{n,+}(k_x,k_y)- S_{n,+}(k_x,k_y) \simeq \int\int A(x,y) 2j\sin\left( 2\pi\Delta f(x,y)\frac{k_x}{\gamma G_x} \right) = \frac{2}{\gamma G_x} {\cal F} \left[ \frac{ \partial A(x,y) \Delta f(x,y)}{\partial x} \right] $$
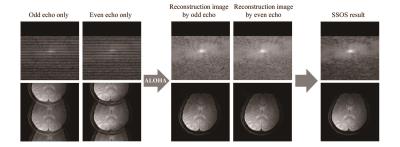
where $$$A(x,y) = m(x,y)e^{j2\pi \Delta f(x,y) (TE+ (n-N/2)ESP )}.$$$ Note that the difference between two virtual k-space data generates a sparse image because the partial differential term is basically a total variation (TV) operator. Based on this property, we used ALOHA to interpolate the k-space lines. Specifically, we can show that the concatenated matrix $$$\mathcal{Y} =\begin{bmatrix} \mathcal{H}\left(S_{n,+}\right) & \mathcal{H}\left(S_{n,-}\right) \end{bmatrix}$$$ has low ranked, so we can fill in the missing lines by using a low rank structured matrix completion algorithm for . Then, the final ghost-free image can be obtained as a sum-of-squares(SSoS) of the even and odd line image reconstructions (Fig.2).
Results and Conclusion
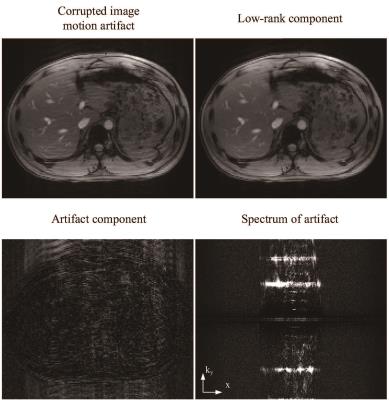
Figure 3 illustrates motion artifact correction using ALOHA. Here, the motion components from sudden movement are decomposed as sparse component in k-space. Figure 4 shows a representative example of EPI ghost correction using ALOHA, which clearly removes the ghost artifact without any calibration data. Extensive experimental results further confirmed that the proposed algorithm can correct MR artifacts including herringbone (crisscross), motion, zipper artifacts, and EPI ghost artifact without image distortion.Acknowledgements
This work is supported by Korea Science and Engineering Foundation, Grant number NRF-2016R1A2B3008104.References
[1] JC Ye, JM Kim, KH Jin and K Lee, "Compressive sampling using annihilating filter-based low-rank interpolation", IEEE Trans. on Information Theory, vol. 63, no. 2, pp.777-801, Feb. 2017.
[2] KH Jin, D Lee, and JC Ye. "A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix." IEEE Transactions on Computational Imaging 2.4 (2016): 480-495.
[3] KH Jin et al, "MRI artifact correction using sparse+ low‐rank decomposition of annihilating filter‐based hankel matrix." Magn Reson Med. 2016 Jul 28. doi: 10.1002/mrm.26330.
[4] J Lee et al, "Reference-free single-pass EPI Nyquist ghost correction using annihilating filter-based low rank Hankel matrix (ALOHA)", Magnetic Resonance in Medicine, 10.1002/mrm.26077, Feb. 17, 2016.
[5] D Lee et al, "Acceleration of MR parameter mapping using annihilating filter-based low rank Hankel matrix (ALOHA)", Magnetic Resonance in Medicine, 10.1002/mrm.26081, Jan. 1, 2016.
Figures