Gradients
1Yale University, New Haven, CT, United States
Synopsis
New developments in gradient technology have brought higher resolution, improved diffusion imaging, and entirely novel encoding schemes. This lecture will review the hardware, methodology and results of some of the newest techniques using non-traditional gradient hardware.
Highlights
- Developments in linear gradient technology include increased power, reduced ramping times, and advanced shim technologies, including matrix arrays which can be used for shimming, RF, and even image encoding with linear or nonlinear gradients
- Nonlinear gradient (NLG) imaging refers to encoding with fields that vary nonlinearly in space, so the linear equivalence between frequency and space no longer applies
- Most research in NLG imaging has focused on enhanced parallel imaging, but other applications include reduced PNS, targeted volume imaging, and imaging in the inhomogeneous fields of some portable MRI systems.
Target Audience
Physicists and engineers interested in new technologies that use non-traditional gradient hardware for higher resolution or faster imagingEducational Objectives
- Review developments in linear imaging technology and their application
- Understand basic concepts in nonlinear gradient imaging
- Describe current and future applications of switchable nonlinear gradients
Non-traditional Linear Gradients
In recent years, high power gradients have become widely available commercially, and extremely high power gradients have come online for research. Images from the Connectome Project gradients have dramatically improved the resolution and SNR of diffusion based modalities, with a huge range of applications. (1) For sequences limited by switching, rather than amplitude, head only gradient inserts allow for faster switching with reduced PNS. (2)
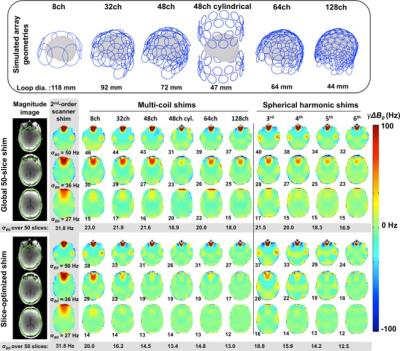
In addition, a number of developments have been made in shimming technology. (Figure 1) Traditional shim inserts based on spherical harmonics improve resolution and are especially important in high field imaging. (3) In addition, a number of groups are pursuing matrix coil solutions with broad flexibility to correct for high order inhomogeneities, and RF can be incorporated into the same hardware. (4-6) While these flexible arrays are still primarily used for correcting homogeneity in the B0 field, early demonstrations show they are also able to generate fields strong enough for image encoding with either linear or nonlinear gradients.
Basics of Nonlinear Gradient Imaging
Nonlinear gradient (NLG) imaging uses fields that vary nonlinearly in space to localize or encode spins. Though they were first studied for their potential to reduce peripheral nerve stimulation, most research on NLG encoding has focused on its ability to improve parallel imaging by complementing the nonlinear encoding provided by multichannel receivers. (7-9) In addition, several groups have shown that nonlinear encoding promotes incoherence in undersampling artifacts, which improves the performance of advanced reconstruction methods, such as compressed sensing and low-rank matrix recovery. (10, 11) Tailored FOV selection has shown promise both in slice selection and in plane. (12-14) Finally, portable MRI with inhomogeneous B0 fields is a rapidly developing application of this field. (15, 16)
NLG imaging is generally accomplished with a separate gradient insert that sits inside the magnet bore. The first gradients were designed and wound to generate specific field geometries, such as 2nd order linear harmonics. (17, 18) More recently, researchers have explored designs based on much larger arrays of localized coils. With appropriate combinations, these can generate a wide range of gradient shapes. (19) Because the NLGs are generally run in tandem with linear gradients, each NLG shape requires a separate amplifier, cooling system, and waveform generator, which must be synchronized with other parts of the pulse sequence. Thus, while 84 channel arrays have been built, at any given time the coils must be wired into a much smaller set of fixed combinations, equal to the number of amplifiers. However, with minor modification, these gradient arrays can generate both low and high order spherical harmonics, as well as arbitrary combinations of these.
Images acquired with NLG encoding are often reconstructed by solving for the image that is consistent with the encoding and data, minimizing the L2 norm of the residual. That approach can seamlessly incorporate nonidealities in the gradient shape, RF receiver sensitivities, and known timing errors. Both Kaczmarz and conjugate gradients algorithms have been used successfully for this purpose. Though much slower than FFT, these algorithms can be massively parallelized with GPU programming, leading to clinically viable reconstruction times on the order of 1 minute.
Nonlinear Gradients to Overcome Limits on Gradient Switching
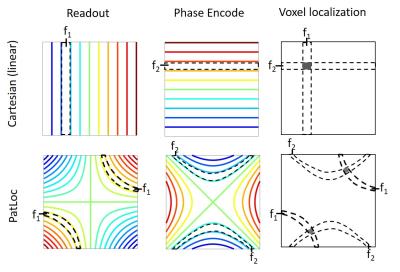
Imaging with nonlinear gradients was proposed several times in the literature, (20, 21) but in the past decade it was first reintroduced as a means of overcoming current limits on PNS stimulation. (7) The PatLoc sequence was designed in direct analogy with rectilinear spin-warp encoding: frequency and phase encoding with two different field shapes assigns spins to the intersection of frequency bands in each field shape (i.e., solves for what spin population was evolving at (fread +/- Δf, fphase +/- Δf), where Δf = BW/Nsamples). (Figure 2) In PatLoc, the frequency and phase encoding fields are 2nd order spherical harmonics known as C2 and S2. Since there are two spatial bands associated with each frequency band, coil sensitivity is required to resolve this ambiguity, even without undersampling. Furthermore, even though bands are uniformly distributed in frequency, the width of each band in physical space varies across the FOV, and their intersection is not square. These lead to spatially varying resolution and non-rectangular voxel shape, which are general features of all NLG imaging modalities.Nonlinear Gradients for Parallel Imaging
O-Space was the first NLG imaging strategy designed to enhance parallel imaging. (8) O-Space aimed to complement the azimuthal spatial encoding of typical RF head arrays with the radially varying encoding of the Z2 gradient. (Figure 3a) It also introduced the mixing of both linear and nonlinear gradients for spatial encoding. A radial-like sequence played out on the linear gradients is played in conjunction with a constant amplitude NLG which leads to projection imaging with the fields shown in Figure 3b. This method showed tremendously improved acceleration over Cartesian SENSE, and more diffuse artifacts compared to undersampled radial. Furthermore, whereas radial undersampling artifacts can be exacerbated by increasing the resolution in the readout direction, O-Space images are improved by oversampled readouts, which can be acquired with virtually no increase in scan time. (22)
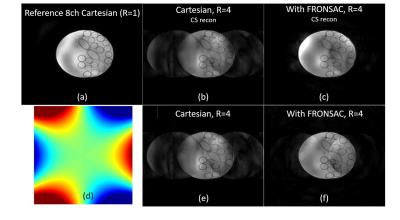
A number of other methods have since been proposed to improve the efficiency of gradient encoding in the context of parallel imaging. Encoding has been shown via pure projection imaging (23), projection with phase encoding (24), and arbitrary trajectories on all gradient channels (25). More recently, highly dynamic trajectories where the nonlinear gradients provide a small perturbation to standard encoding were introduced with the FRONSAC method. (26) Preliminary experiments with this technique have shown obvious and dramatic improvements in image quality from the addition of NLG encoding, while retaining many features of the underlying Cartesian imaging sequence. (Figure 4) It is also the first technique based on NLG acquisition of k-space.
Though the idea to improve parallel imaging with NLG encoding came from geometric considerations in physical space, their role in reducing undersampling artifacts is more succinctly described in k-space. (27) NLG moment spreads the sampling function in k-space, similar to the nonlinear profiles of multichannel receiver coils. By creating a small distribution in the sampling of k-space, gaps in the Cartesian trajectory are better sampled, and images can thus be reconstructed more accurately from undersampled data. When also encoding with multichannel receivers, the sampling in k-space is the convolution of these functions, so a judicious choice can improve sampling in the gaps of the linear trajectory. (Figure 5)
Other Features
Another interesting feature of NLG encoding, which emerged from its study as a parallel imaging modality, is its suitability for advanced reconstruction techniques. In particular, it’s been shown that the NLG in O-Space decreases coherence between the measurement basis and a wavelet sparsifying basis, leading to improved compressed sensing. (10) The same phenomenon has been shown for FRONSAC imaging. Even NLG prephasing of images that are otherwise normally encoded with linear gradients improves compressed sensing reconstruction. (11)
NLGs have also been explored as a means to localize signal from a tailored target volume. Since many NLG shapes have a relatively flat saddle surrounded by steep fields, this arrangement can be used to preferentially dephase signal outside that region. (28) In addition, nonlinear gradients can be used to generate tailored slice selection for more efficient encoding in the region of interest. (12, 14)
Finally, the push for portable MRI systems has renewed exploration of highly inhomogeneous B0 fields, which are equivalent to large static nonlinear gradients. Several solutions have been proposed to incorporate these fields into the image encoding process. For example, projection encoding with C2 and S2 fields was used to generate the first experimental images from a physically rotating permanent magnet. (15) Spatiotemporal excitation is a very different approach to recovering image encoding in the presence of large static nonlinear gradients, which often result from strong and compact magnet designs. (16)
Acknowledgements
Dr. Galiana gratefully acknowledges funding from NIH K01 CA 168977.References
1.McNab JA, Edlow BL, Witzel T, Huang SY, Bhat H, Heberlein K, Feiweier T, Liu K, Keil B, Cohen-Adad J, Tisdall MD, Folkerth RD, Kinney HC, Wald LL. The Human Connectome Project and beyond: initial pplications of 300 mT/m gradients. Neuroimage. 2013;80:234-45. doi: 10.1016/j.neuroimage.2013.05.074. PubMed PMID: 23711537; PMCID: PMC3812060.
2. Tan ET, Lee SK, Weavers PT, Graziani D, Piel JE, Shu Y, Huston J, 3rd, Bernstein MA, Foo TK. High slew-rate head-only gradient for improving distortion in echo planar imaging: Preliminary experience. Journal of magnetic resonance imaging : JMRI. 2016;44(3):653-64. doi: 10.1002/jmri.25210. PubMed PMID: 26921117; PMCID: PMC4983491.
3. Winkler SA, Schmitt F, Landes H, DeBever J, Wade T, Alejski A, Rutt BK. Gradient and shim technologies for ultra high field MRI. Neuroimage. 2016. doi: 10.1016/j.neuroimage.2016.11.033. PubMed PMID: 27915120.
4. Juchem C, Umesh Rudrapatna S, Nixon TW, de Graaf RA. Dynamic multi-coil technique (DYNAMITE) shimming for echo-planar imaging of the human brain at 7 Tesla. Neuroimage. 2015;105:462-72. doi: 10.1016/j.neuroimage.2014.11.011. PubMed PMID: 25462795; PMCID: 4262558.
5. Stockmann JP, Witzel T, Keil B, Polimeni JR, Mareyam A, LaPierre C, Setsompop K, Wald LL. A 32-channel combined RF and B shim array for 3T brain imaging. Magn Reson Med. 2015. doi: 10.1002/mrm.25587. PubMed PMID: 25689977.
6. Truong TK, Darnell D, Song AW. Integrated RF/shim coil array for parallel reception and localized B0 shimming in the human brain. Neuroimage. 2014;103:235-40. doi: 10.1016/j.neuroimage.2014.09.052. PubMed PMID: 25270602; PMCID: 4312247.
7. Hennig J, Welz AM, Schultz G, Korvink J, Liu Z, Speck O, Zaitsev M. Parallel imaging in non-bijective, curvilinear magnetic field gradients: a concept study. Magnetic Resonance Materials in Physics, Biology and Medicine. 2008;21(1):5--14.
8. Stockmann JP, Ciris PA, Galiana G, Tam L, Constable RT. O-Space imaging: Highly efficient parallel imaging using second-order nonlinear fields as encoding gradients with no phase encoding. Magnetic Resonance in Medicine. 2010;64(2):447--56.
9. Multi-dimensional encoded (MDE) magnetic resonance imaging Multi-dimensional encoded (MDE) magnetic resonance imaging2011.
10. Tam LK, Galiana G, Stockmann JP, Tagare H, Peters DC, Constable RT. Pseudo-random center placement O-space imaging for improved incoherence compressed sensing parallel MRI. Magn Reson Med. 2014. doi: 10.1002/mrm.25364. PubMed PMID: 25042143; PMCID: 4297603.
11. Puy G, Marques J, Gruetter R, Thiran J, Van De Ville D, Vandergheynst P, Wiaux Y. Spread spectrum magnetic resonance imaging. IEEE Transactions on Medical Imaging. 2011;31(3):586-98. doi: 10.1109/tmi.2011.2173698.
12. Weber H, Gallichan D, Schultz G, Cocosco CA, Littin S, Reichardt W, Welz A, Witschey W, Hennig J, Zaitsev M. Excitation and geometrically matched local encoding of curved slices. Magn Reson Med. 2013;69(5):1317-25. doi: 10.1002/mrm.24364. PubMed PMID: 22711656.
13. Witschey W, Cocosco C, Gallichan D, Schultz G, Weber H, Welz A, Hennig J, Zaitsev M. Localization by nonlinear phase preparation and k-space trajectory design. Magnetic Resonance in Medicine. 2012;67(6):1620-32.
14. Kopanoglu E, Constable RT. Radiofrequency pulse design using nonlinear gradient magnetic fields. Magn Reson Med. 2015;74(3):826-39.
15. Cooley CZ, Stockmann JP, Armstrong BD, Sarracanie M, Lev MH, Rosen MS, Wald LL. 2D Imaging in a Lightweight Portable MRI Scanner without Gradient Coils. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2015;73(2):872-83. doi: 10.1002/mrm.25147. PubMed PMID: PMC4257909.
16. Snyder ALS, Corum CA, Moeller S, Powell NJ, Garwood M. MRI by steering resonance through space. Magn Reson Med. 2014;72(1):49-58. PubMed PMID: 23913527; PMCID: 4285333.
17. Stockmann JP, Galiana G, Tam L, Juchem C, Nixon TW, Constable RT. In vivo O-Space imaging with a dedicated 12 cm Z2 insert coil on a human 3T scanner using phase map calibration. Magn Reson Med. 2013;69(2):444-55. doi: 10.1002/mrm.24282. PubMed PMID: 22585546; PMCID: 3491108.
18. Schultz G, Ullmann P, Lehr H, Welz AM, Hennig J, Zaitsev M. Reconstruction of MRI data encoded with arbitrarily shaped, curvilinear, nonbijective magnetic fields. Magnetic Resonance in Medicine. 2010;64(5):1390-403.
19. Jia F, Schultz G, Testud F, Welz AM, Weber H, Littin S, Yu H, Hennig J, Zaitsev M. Performance evaluation of matrix gradient coils. MAGMA. 2016;29(1):59-73. doi: 10.1007/s10334-015-0519-y. PubMed PMID: 26667966.
20. Ito S, Yamada Y. Alias-free image reconstruction using Fresnel transform in the phase-scrambling Fourier imaging technique. Magnetic Resonance in Medicine. 2008;60(2):422--30.
21. Patz S, Hrovat MI, Pulyer YM, Rybicki FJ. Novel encoding technology for ultrafast MRI in a limited spatial region. International Journal of Imaging Systems and Technology. 2012;10(3):216-24. doi: 10.1002/(SICI)1098-1098(1999)10:3<216::AID-IMA3>3.0.CO;2-Q.
22. Wang H, Tam L, Kopanoglu E, Peters D, Constable RT, Galiana G. O-Space with high resolution readouts outperforms radial imaging. Magnetic Resonance in Medicine. 2017;37(April):107-15.
23. Tam LK, Stockmann JP, Galiana G, Constable RT. Null Space Imaging: Nonlinear Magnetic Encoding Fields Designed Complementary to Receiver Coil Sensitivities for Improved Acceleration in Parallel Imaging. Magnetic Resonance in Medicine. 2011;68(4): 1166-75.
24. Gallichan D, Cocosco C, Dewdney A, Schultz G, Welz A, Hennig J, M. Z. Simultaneously driven linear and nonlinear spatial encoding fields in MRI. Magnetic Resonance in Medicine. 2011;65(3):702-14.
25. Lin FH. Multidimensionally encoded magnetic resonance imaging. Magn Reson Med. 2013;70(1):86-96. Epub 2012/08/29. doi: 10.1002/mrm.24443. PubMed PMID: 22926830.
26. Wang H, Tam LK, Constable RT, Galiana G. Fast rotary nonlinear spatial acquisition (FRONSAC) imaging. Magn Reson Med. 2016;75(3):1154-65. doi: 10.1002/mrm.25703. PubMed PMID: 25950279; PMCID: PMC4637004.
27. Galiana G, Stockmann JP, Tam L, Peters D, Tagare H, Constable RT. The role of nonlinear gradients in parallel imaging: A k-space based analysis. Concepts in Magnetic Resonance Part A.40A(5):253-67. doi: 10.1002/cmr.a.21243.
Figures
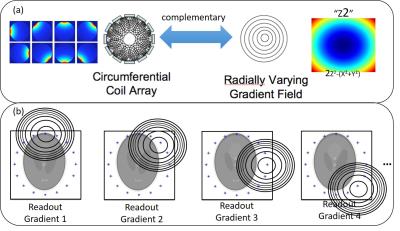
(a) O-Space was designed to enhance parallel imaging by complementing azimuthal coil profiles with a radially varying gradient field.
(b) Each O-Space readout is a projection under a radially varying gradient. The center of this gradient is different in different acquisitions, forming a circle around the FOV.