Synopsis

MRI is capable of providing flexible soft tissue contrast and real-time guidance of interventions. Real-time information about the motion of tissues and devices is essential to provide feedback for physician and robotic control of MRI-guided interventions. In this work, a new motion prediction algorithm using MRI-based motion tracking and multi-rate Kalman filtering is proposed to provide accurate and real-time motion information. Experiments and simulations show that Kalman filtering with expectation maximization training and multi-rate data fusion is able to achieve low motion prediction error. This new algorithm has potential in providing real-time feedback information for MRI-guided interventions.

Introduction

MRI-guided interventions in the upper abdomen are challenged by limited access to the subject inside the scanner bore and constant motion¹. MRI-compatible robotic systems are a potential strategy to assist physicians and overcome these challenges. Real-time knowledge of tissue and device motion should be provided as feedback for physician decision-making and computerized robotic control. In this work, we lay the foundation for human-robot collaborative interventions by designing and evaluating a real-time MRI-based motion prediction algorithm that uses multi-rate Kalman filtering (KF) to overcome latencies².

Theory

KF: The KF is a simple recursive solution for state estimation^3,4. Reliable calibration of motion and measurement uncertainty parameters is essential. Therefore, we propose to test two calibration methods: KF using expectation maximization (KFEM)⁵ and extended KF (EKF)⁶. Their estimations are updated in a predictor-corrector algorithm^4,7 to predict the motion state at a future time point t+dτ (Fig.1b).

Multi-rate KF: In addition to using fully reconstructed MR images for motion tracking and prediction, higher temporal rates can be achieved using subsets of the same data (e.g., low-resolution images reconstructed from fewer radial spokes in a golden-angle-ordered acquisition⁸). Therefore, we investigated multi-rate KF (MRKF) to improve motion prediction by fusing data with low and high temporal rates (Fig.1c). The estimation x_k* was calculated by^9,10:

$$x_{k}^{*}=M^{*}K\left(z_{k}^{*}-x_{s}\right)+x_{k}\qquad M^{*}=\prod_{i=0}^N\left(I-HK_{k-i}\right)F$$

H is the measurement matrix, F is the state transition matrix and K is the Kalman gain matrix.

Methods

The overall motion prediction framework for feedback control is shown in Fig.1.

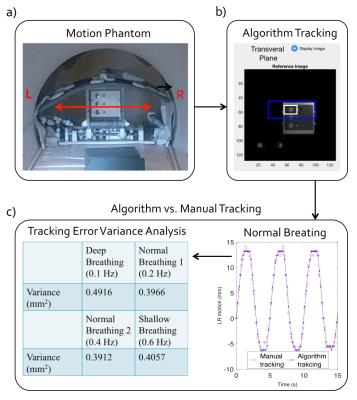
Motion Tracking: The proposed framework (Fig.1a) was implemented and interfaced to a 3T MRI system (Prisma, Siemens) for online processing. An MR image-based navigation algorithm is used to track multiple targets with low computation overhead¹¹. The algorithm tracking performance was evaluated with an MR-compatible motion phantom (Fig.2a). The algorithm tracking error was computed with respect to reference manual tracking results and used to calibrate measurement noise for KF simulations and processing (Fig.2b).

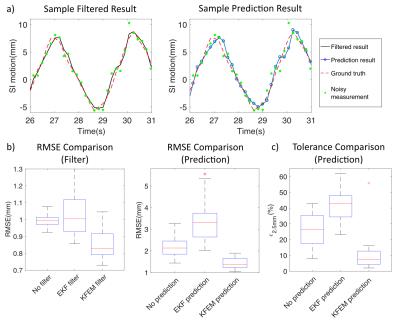
KF Simulations: Upper abdominal images were acquired from healthy volunteers at 3T (Prisma, Siemens) with 5.6 frames/sec (dt = 179ms/frame), 2.5-mm spatial resolution, and 160x160 matrix size. Extracted motion waveforms were used as the ground truth and white Gaussian noise was added to simulate measurement noise⁵ (Fig.3a). Applying KFEM¹² and EKF¹³, we compared the root mean square error (RMSE) of filtered motion at each time point and prediction at the next time point (dτ=dt). Additionally, the percentage of prediction error >2.5mm (ε_2.5(%)) was compared. The 2.5 mm tolerance represents <1 pixel error for these images and corresponds to the required accuracy for clinically relevant targets of >5mm diameter.

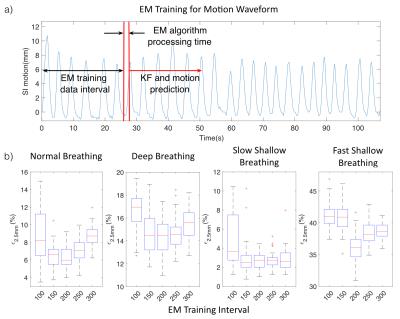
EM Training: KF processing time is negligible (5-10ms), but the requirement of training data and processing for EM may increase latencies. Therefore, using 4 typical motion waveforms, the optimal amount of data for EM training is investigated by comparing the prediction error in the 400 time points after training.

MRKF Simulations: MR images at high temporal rate (reference) were retrospectively undersampled to high temporal rate (HTR)-low spatial resolution (LSR) images and low temporal rate (LTR)-high spatial resolution (HSR) images (Fig.5a-b). We performed simulations for MRKF prediction and evaluate RMSE and ε_2.5 to compare with KF prediction.

Results and Discussion

Motion Tracking: Algorithm and manual tracking results are shown in Fig.2b-c. The average variance of the tracking error is 0.423 mm². In vivo motion may have non-rigid components; therefore, the additive noise variance is increased to 1 mm² in the KF simulations.

KF Simulations: The filtered and 1-frame prediction result from KFEM has the least RMSE and ε_2.5 (Fig.3b). It is more practical than EKF because the performance is less sensitive to initial parameter selection, but the challenge is additional EM training.

EM Training: The optimal EM training interval is 150-200 frames (Fig.4b) and the average processing time is 0.8s. To overcome training latencies in practice, an adaptive strategy can be implemented to trigger EM training when the motion prediction error exceeds a threshold.

MRKF Simulations: MRKF achieves lower prediction error than KF using only HTR-LSR or LTR-HSR (Fig. 5b). This shows the potential of MRKF to improve the accuracy and temporal-rate of motion prediction by incorporating MR images with different rates, which can be obtained by reconstructing both LTR-HSR and HTR-LSR images from the same data (e.g., radial MRI).

Conclusion

Acknowledgements

References

1. Ries M, De Senneville BD, Roujol S, Berber Y, Quesson B, Moonen C. Real-time 3D target tracking in MRI guided focused ultrasound ablations in moving tissues. Magn Reson Med 2010;64:1704–12.

2. Campbell-Washburn AE, Faranesh AZ, Lederman RJ, Hansen MS. Magnetic Resonance Sequences and Rapid Acquisition for MR-Guided Interventions. Magn Reson Imaging Clin NA 2015;23:669–79.

3. Welch G, Bishop G. An introduction to the Kalman filter. In: Proceedings of the Siggraph Course, Los Angeles, 2001.

4. Bar-Shalom Y, Li XR, Kirubarajan T. Estimation with applications to tracking and navigation: theory algorithms and software. John Wiley & Sons, 2004.

5. Sharp, GC, Jiang SB, Shimizu S, Shirato H. Prediction of respiratory tumour motion for real-time image-guided radiotherapy. Phys Med Biol 2004;49:425–440.

6. Ramrath L, Schlaefer A, Ernst F, Dieterich S, Schweikard A. Prediction of respiratory motion with a multi-frequency based extended Kalman filter. In: Proceedings of the 21st international conference and exhibition on computer assisted radiology and surgery (CARS’07), Germany, 2007.

7. Spincemaille P, Nguyen TD, Prince MR, Wang Y. Kalman filtering for real-time navigator processing. Magn Reson Med 2008;60:158–68.

8 Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE Trans Med Imaging 2007;26:68–76.

9 Alexander, HL. State Estimation for Distributed Systems with Sensing Delay. In: SPIE , Orlando, 1991;Data Structures and Target Classification 1470:103–111.

10 Larsen TD, Andersen NA, Ravn O, Poulsen NK. incorporation of time delayed measurements in a discrete-time Kalman filter. IEEE Conf Decis Control 1998;4:3972–7.

11 Wu HH, Gurney PT, Hu BS, Nishimura DG, McConnell M V. Free-breathing multiphase whole-heart coronary MR angiography using image-based navigators and three-dimensional cones imaging. Magn Reson Med 2013;69:1083–93.

12 Murphy, K,. Kalman Filter Toolbox For Matlab. 2004. http://www.cs.ubc.ca/~murphyk/Software/Kalman/kalman.html

13 Särkkä, S., Hartikainen, J., & Solin, A. EKF/UKF Toolbox for Matlab V1.3. 2011. http://becs.aalto.fi/en/research/bayes/ekfukf/