Synopsis

Head motion poses a significant problem in MRSI experiments, especially for 1H-MRSI of the brain performed without water or lipid suppression. In this work we propose a practical method specifically designed to track head motion and correct for its effects on 1H-MRSI data acquired without water suppression. By using the companion spectroscopic water signals, we are able to track head motion with navigators collected in circular and linear trajectories. A specialized data processing scheme is also proposed for processing the navigator data along with the unsuppressed spectroscopic water signals to determine the motion parameters.

Introduction

Head motion is a significant problem in practical MRSI experiments, which results in a variety of artifacts (e.g. ghosting artifacts), and can induce $$$B_0$$$ field inhomogeneity changes.$$$^{1-4}$$$ This problem is particularly serious for 1H-MRSI of the brain performed without water/lipid suppression. Even small head movements can make removal of the unsuppressed water and lipid signals extremely difficult, rendering high-quality spatiospectral reconstructions of the metabolic signals of interest impossible.

We propose a practical method specifically designed to track head motion and correct its effects on 1H-MRSI data of the brain performed without water suppression. Using the unsuppressed water signals, we are able to track head motion with circular and linear navigators. A specialized data processing scheme is also proposed for processing the navigator data along with the unsuppressed water signals to determine the motion parameters.

Methods

Data Acquisition

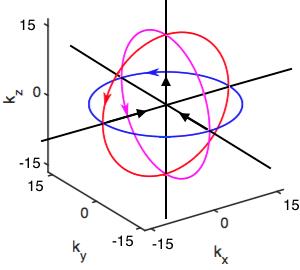
The data acquisition scheme is characterized by the insertion of two sets of navigators (a) three perpendicular orbital navigators, and (b) three perpendicular linear navigators (Fig. 1) into a 1H-MRSI acquisition. All six navigators can be acquired in a single $$$T_{\mathrm{R}}$$$, every $$$NT_R$$$. For our applications we have $$$T_{\mathrm{R}}$$$=210ms and $$$N=10$$$ to allow for motion tracking motion every 2.1 seconds.

Motion Estimation

We treat head movements as rigid body motion. Defining translation and rotations about the $$$x$$$, $$$y$$$, and $$$z$$$-axes as $$$\Delta\mathbf{r}=(\Delta x,\Delta y,\Delta z)$$$ and $$$\Delta\boldsymbol{\theta}=\left(\Delta\theta_x, \Delta\theta_y, \Delta\theta_z\right)$$$ respectively, the images before and after motion $$$\rho_1(\mathbf{r})$$$ and $$$\rho_2(\mathbf{r})$$$, with Fourier transforms $$$s_1(\mathbf{k})$$$ and $$$s_2(\mathbf{k})$$$, are related by,$$\rho_2\left(\mathbf{r}\right)=\rho_1\left(\mathrm{R}_{\Delta\theta}\mathbf{r}+\Delta\mathbf{r}\right)$$and$$s_2(\mathbf{k})=s_1(\mathrm{R}_{\Delta\theta}\mathbf{k})e^{-i2\pi \mathrm{R}_{\Delta\theta}\mathbf{k}\cdot\Delta\mathbf{r}}$$ where $$$\mathrm{R}_{\Delta\theta}$$$ is the rotation matrix dependent on $$$\Delta\boldsymbol{\theta}$$$. Denoting the the $$$i^{th}$$$ k-space sampling location of the navigator trajectory as $$$\mathbf{k}_i$$$ and the number of navigator samples as $$$M$$$, the motion estimation problem is to determine $$$\Delta\mathbf{r}$$$ and $$$\Delta\boldsymbol{\theta}$$$, from $$$\mathbf{d}_1=\{s_1(\mathbf{k_i})\}_{i=1}^M$$$, $$$\mathbf{d}_2=\{s_2(\mathbf{k_i})\}_{i=1}^M$$$.

As shown above, $$$\mathbf{d}_2$$$ is related to $$$\mathbf{d}_1$$$ by a rotation of the sampling trajectory $$$\mathcal{K}=\{\mathbf{k}_i\}_{i=1}^M$$$, and an added linear phase. For an orbital in the $$$k_x$$$-$$$k_y$$$ plane with radius $$$k$$$ and sampling rate $$$\Delta t$$$,$$\mathbf{k}_i=k\begin{pmatrix}\cos(i\Delta t)\\ \sin(i\Delta t)\\ 0 \end{pmatrix}$$and the rotated trajectory $$$\mathcal{K}'=\{\mathbf{k}_i'\}_{i=1}^M$$$ will have$$\mathbf{k}_i'=\mathrm{R}_{\Delta\theta}\mathbf{k}_i=k\begin{pmatrix}\cos(i\Delta t)\cos\Delta\theta_y\cos\Delta\theta_z+\sin(i\Delta t)\left[ \cos\Delta\theta_z \sin\Delta\theta_x \sin\Delta\theta_y-\sin\Delta\theta_z \cos\Delta\theta_x\right]\\ \cos(i\Delta t)\cos\Delta\theta_y \sin\Delta\theta_z+\sin(i\Delta t)\left[\sin\Delta\theta_z\sin\Delta\theta_x\sin\Delta\theta_y+\cos\Delta\theta_z\cos\Delta\theta_x\right]\\ \sin(i\Delta t)\sin\Delta\theta_x\cos\Delta\theta_y-\cos(i\Delta t)\sin\Delta\theta_y\end{pmatrix}.$$Similar expressions can be derived for the other orbitals. If any two angles are zero, the modulus of the two readouts along the orbital centered on the remaining axis will be related by a circular shift, which can be robustly determined.$$$^5$$$ However, when the rotation angles are not multiples of $$$\pi/2$$$, there will be few sampling locations in common between $$$\mathcal{K}$$$ and $$$\mathcal{K}'$$$ making motion estimation a poorly conditioned problem.

We address this issue by using the unsuppressed water signals to generate a reference image $$$\rho_{\mathrm{ref}}(\mathbf r)$$$ (with Fourier transform $$$s_{\mathrm{ref}}(\mathbf{k})$$$). Assuming motion effects during acquisition are small enough that $$$\rho_{\mathrm{ref}}(\mathbf{r}) \approx\rho_1\left(\mathrm{R}_{\phi}\mathbf{r}+\mathbf{b}\right)$$$. We estimate the relative rotation among, $$$\rho_{\mathrm{ref}}(\mathbf{r})$$$, $$$\rho_1(\mathbf{r})$$$, and $$$\rho_2(\mathbf{r})$$$ by iterating between: (a) aligning $$$\rho_{\mathrm{ref}}(\mathbf{r})$$$ according to the current estimate of $$$\Delta\boldsymbol{\theta}$$$, (b) computing $$$\mathbf{d}_{\mathrm{ref}}=\{s_{\mathrm{ref}}(\mathbf{k_i})\}_{i=1}^M$$$, and (c) estimating the circular shifts among $$$|\mathbf{d}_{\mathrm{ref}}|$$$, $$$|\mathbf{d}_1|$$$, and $$$|\mathbf{d}_2|$$$.

Even with $$$\Delta\boldsymbol{\theta}$$$ estimated, phase discrepancies between $$$\rho_{\mathrm{ref}}(\mathbf{r})$$$ and $$$\rho_1\left(\mathrm{R}_{\phi}\mathbf{r}+\mathbf{b}\right)$$$ prevent $$$\Delta\mathbf{r}$$$ from being estimated via the phase difference between $$$\mathbf{d}_{\mathrm{ref}}$$$, $$$\mathbf{d}_1$$$, and $$$\mathbf{d}_2$$$.⁵ We solved this problem by including linear navigators and estimating $$$\Delta\mathbf{r}$$$ from the shift between their image projections.

Motion Correction

Given estimates of $$$\Delta\mathbf{r}$$$ and $$$\Delta\boldsymbol{\theta}$$$, motion correction is performed by incorporating a motion operator into the encoding operator of our model-based reconstruction schemes$$$^6$$$ (e.g. water/lipid removal$$$^7$$$ and image reconstruction⁸).

Results

We acquired in vivo 1H-MRSI data from a human volunteer on a 3T Siemens Trio scanner using a bipolar EPSI sequence.$$$^{8,9}$$$ Two data sets were acquired with FOV = 250x250x72mm$$$^3$$$, BW=167kHz; one with $$$T_{\mathrm{R}}/T_{\mathrm{E}}$$$=210/4ms, matrix size=96x96x24, one with $$$T_{\mathrm{R}}/T_{\mathrm{E}}$$$=310/4ms, matrix size=96x96x24. The subject was instructed to remain still during the first scan and to perform three deliberate head motions during second scan.

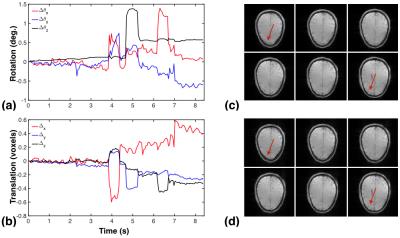
Figure 2 shows the estimated motion parameters and also reconstructions of the water signal with and without motion correction, illustrating our method's ability to track motion and correct its effects.

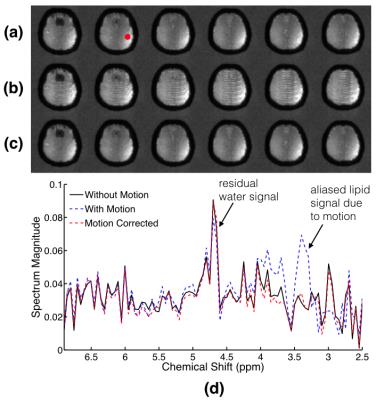
We used a simulation to demonstrate the improvement in water/lipid signal removal provided by our method. Artificially motion-corrupted data were generated from the data acquired without subject motion. After applying our estimation and correction scheme we performed water/lipid signal removal. Figure 3 shows the results, and demonstrates our method enables improved lipid signal removal.

Conclusions

Acknowledgements

References

1. Posse S, Cuenod CA, Le Bihan D, Motion artifact compensation in 1H spectroscopic imagingby signal tracking. J. Magn. Reson. B 1993; 102:222 – 227.

2. Hess AT, Andronesi OC, Tisdall MD, Sorensen AG, van der Kouwe AJW, Meintjes EM, Real-time motion and B0 correction for localized adiabatic selective refocusing (LASER) MRSI using echo planar imaging volumetric navigators. NMR Biomed. 2011; 25:347 – 358.

3. Haupt CI, Kiefer AP, Maudsley AA, In-plane motion correction for MR spectroscopic imaging. Magn. Reson. Med. 1998; 39:749 – 753.

4. Lange T, Maclaren J, Buechert M, Zaitsev M, Spectroscopic imaging with prospective motion correction and retrospective phase correction. Magn. Reson. Med. 2012; 67:1506 – 1514.

5. Fu ZW, Wang Y, Grimm RC, Rossman PJ, Felmlee JP, Riederer SJ, Ehman RL, Orbital navigator echoes for motion measurements in magnetic resonance imaging. Magn. Reson. Med. 1995; 34:746 – 753.

6. Batchelor PG, Atkinson D, Irarrazaval P, Hill DLG, Hajnal J, Larkman D, Matrix descriptionof general motion correction applied to multishot images. Magn. Reson. Med. 2005; 54:1273 –1280.

7. Ning Q, Ma C, Lam F, Clifford B, Liang ZP, Removal of nuisance signal from sparsely sampled 1H-MRSI data using physics-based spectral bases. Proc. Int. Symp. Magn. Reson. Med., Singapore, 2016; 2361.

8. Lam F, Ma C, Clifford B, Johnson CL, Liang ZP, High-resolution 1H-MRSI of the brain using SPICE: data acquisition and image reconstruction. Magn. Reson. Med. 2016; 76:1059 – 1070.

9. Sheikh MA, Lam F, Ma C, Clifford B, and Liang ZP, Rapid high-resolution 1H-MRSI of the brain based on FID acquisitions. Proc. Intl. Soc. Mag. Reson. Med. 2016; 2353.