5525
IRREGULAR SPIRAL ACQUISITION FOR COMPRESSIVE SENSING IN MRSI1Université de Lyon, INSA‐Lyon, Université Claude Bernard Lyon 1, UJM-Saint Etienne, CNRS, Inserm, CREATIS UMR 5220, U1206, F‐69621, LYON, France, Lyon, France, 2Siemens Healthineers, Saint-Denis, France
Synopsis
Magnetic resonance spectroscopic imaging (MRSI) has multiple interests in clinical practice but it faces quite long acquisition time in practice which limits their use in a clinical environment. In this work, a new fast Magnetic Resonance Spectroscopic image acquisition method, based on Compressed Sensing and the a priori known support of the metabolites chemical shift, is introduced and evaluated based on a k-t space spiral sampling. In the real-world noisy scenario the error in the recovered spectrum highly depends on the acquired samples. We reduce this error to an acceptable level by selecting irregularly the samples using the Sequential Backward Selection algorithm. Our method has been applied on an in vivo 31P acquisition, to prove the feasibility of the proposed approach.
Introduction
Magnetic resonance spectroscopic imaging (MRSI) has multiple interests in
clinical practice but it faces long acquisition time in practice which limits
their use in clinical settings. In this work, a new fast Magnetic Resonance
Spectroscopic image acquisition method is introduced and evaluated based on a
k-t space spiral sampling. Compressed
sensing (CS) is a way to reduce significantly the number of samples acquired
below the Nyquist-Shannon criterion. The sparsity of the signal is mandatory
for the signal reconstruction using CS. In in
vivo MR spectroscopy, the chemical shift of the different chemical
compounds is a priori known. Then the
nonzero components of the spectrum of each pixel are recovered using an
over-determined least square problem. When data are noise-free the recovered
spectrum is exact. In the real-world noisy scenario the error in the recovered
spectrum highly depends on the acquired samples. We reduce this error to an
acceptable level by selecting irregularly the samples using the Sequential Backward
Selection algorithm. Our method has been applied on an in vivo 31P
acquisition, to prove the feasibility of the proposed approach.
Methods
2.1 CS by Least- Square
Problem statement: given the sampled time domain FID signal y related to a kx-ky point in the discrete k space, find its non-zero spectrum samples in its a priori know support S. We solve, by the Least Square method, the over determined equation yp = Axs where A is a pxm matrix obtain by selecting from the discrete Fourier transform matrix F the p rows which correspond to the p-acquired elements from y (noted yp) and the m columns corresponding to the known support spectrum xs.
The subsampling of the FID signal results in a reconstruction error due to noise magnification. Fortunately [3] proposes to minimize this noise amplification by selecting the sample in y with an algorithm known as ‘Sequential Backward Selection’ (SBS), it results an irregular sampling.
2.2 Implementation method
The spiral encoding sequence for MRSI uses successive time varying gradients during the acquisition time period which trace successive spirals in the kx-ky space. One time sample is acquired at each spiral (kx-ky space). If one spiral length time is larger than the temporal resolution required to reconstruct the spectroscopic bandwidth, we have to do temporal interleaves to acquire each necessary time point. This technique consists in applying at each pulse Repetition Time our successive spirals for the acquisition with a delayed time proportionally to the temporal resolution (Fig.1).
Two sampling strategies were implemented and compared: A) the ‘Conventional spiral sampling’ B) the SBS-based irregular sampling for spiral trajectories with a reduction factor of 4 (4 times less time samples than A)).
With SBS, the number of temporal interleaves can be significantly reduced, and the number of excitation can be reduced depending on the length of a spiral. The gain reduction of the acquisition time can be deduced. Both approaches were tested on a 31P MR spectroscopy in vivo data. This data was acquired on a 3T Siemens Prisma on the quadriceps of a man, using the conventional phase-phase encoding. The acquired Cartesian k-spaces were made spiral by calculating the theoretical positions of the samples in a k-space sampled with a spiral [5]. Then, our algorithm was used to reconstruct the spatially distributed spectra with the conventional spiral sampling and the SBS-based one (Fig.2).
Results
In Fig.3, it is represented the in vivo image (t=0) acquired with a conventional phase-phase encoding and the image we would have with a spiral sampling. From a pixel of the left yellow circle, The acquired 31P spectrum is shown Fig.4(a), the spectrum we would have; Fig.4(b) using a conventional spiral MRSI sampling, Fig.4(c) a SBS-based spiral sampling. The Signal to Reconstruction Error Ratio (SRER), with the original acquisition as reference, from the acquired in vivo 31P signal, is of 45,7dB for method A) and 20,5dB for method B).Conclusion
We have demonstrated the feasibility of a novel, original way to reduce the scan time by a CS technique based on LS reconstruction and SBS algorithm, acting on the undersampling of the temporal direction. This work represents a novel contribution of the use of the SBS algorithm in the context of fast MRSI acquisition; which differs from [4] in the sense that, here, it is the a priori known spectral support which is used to reduce the scan time and not the spatial support. Here, spatial and spectral information are acquired simultaneously in spiral acquisition while in [4] conventional phase-phase k-space encoding was used.Acknowledgements
This work was supported by the LABEX PRIMES (ANR-11-LABX-0063), program ”Investissements d’Avenir” (ANR-11-IDEX-0007).References
1. Posse, S., et al., MR spectroscopic imaging: principles and recent advances. Journal of magnetic resonance imaging : JMRI, 2013. 37(6): p. 1301-25.
2. Adalsteinsson, E., et al., Volumetric spectroscopic imaging with spiral-based k-space trajectories. Magnetic Resonance in Medicine, 1998. 39(6): p. 889-898.
3. Reeves, S.J. and L.P. Heck. Selection of observations in signal reconstruction. IEEE Trans. Signal Proc. 1995; 43: 788-791
4. Gao Y, Reeves S. Optimal k-space sampling in MRSI for images with a limited region of support. IEEE Trans. Med. Imaging 2000; 19: 1168-1178.
5. J. Fessler, Image Reconstruction Toolbox, https://web.eecs.umich.edu/~fessler/code
Figures
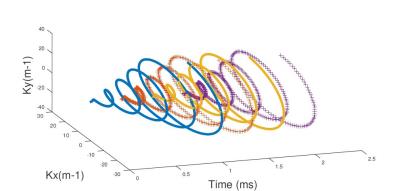
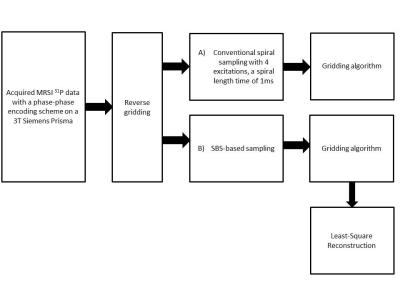
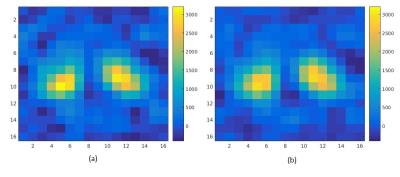

Fig.4 : Spectrum acquired in vivo in (a) with a temporal resolution of 0.25ms and reconstructed with the conventional spiral sampling for MRSI in (b) with a spiral length time of 1ms, 4 temporal interleavings, and the SBS-based one in (b) with a gain reduction of the acquisition time of 2 for the same spiral length. In blue, the acquired signal, in red the reconstructed ones.